河北省唐山市林西中学2018-2019学年八年级上学期期末教学质量检测数学试题(附答案)
文档属性
| 名称 | 河北省唐山市林西中学2018-2019学年八年级上学期期末教学质量检测数学试题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-18 17:10:30 | ||
图片预览



文档简介
唐山市林西中学2018-2019学年第一学期期末教学质量
检测八年级数学试题
考生注意:1.本卷共6页,总分100分,考试时间90分钟。
2.答题前请将密封线左侧的项目填写清楚。
3.答案请用蓝、黑色钢笔或圆珠笔填写。
题号
一
二
三
总分
21
22
23
24
25
26
得分
一、选择题(本大题共12个小题;每小题2分,共24分.在每小题给出的四个选项中只有一项是符合题意,请将正确答案的序号填在题中的括号内)
1.8的相反数的立方根是 ( )
A.-2 B. C. 2 D.-
2.悬针篆文具有较高的历史意义和研究价值,下面四个悬针篆文文字明显不是轴对称图形的是 ( )
3.如图,BD平分∠ABC,AD∥BC,则下列结论正确的是 ( )
A.BC=BD B.AB=AD C.DB=DC D.AD=DC
4.下列各式的计算中,正确的是( )
A.=× B.
C.=×=5 D.3=
5.如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
A.∠B=∠E B.∠A=∠EDF C.∠BCA=∠F D.BC∥EF
6.式子有意义,则实数a的取值范围是( )
A.a≥﹣1 B.a≠2 C.a≥﹣1且a≠2 D.a>2
7.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
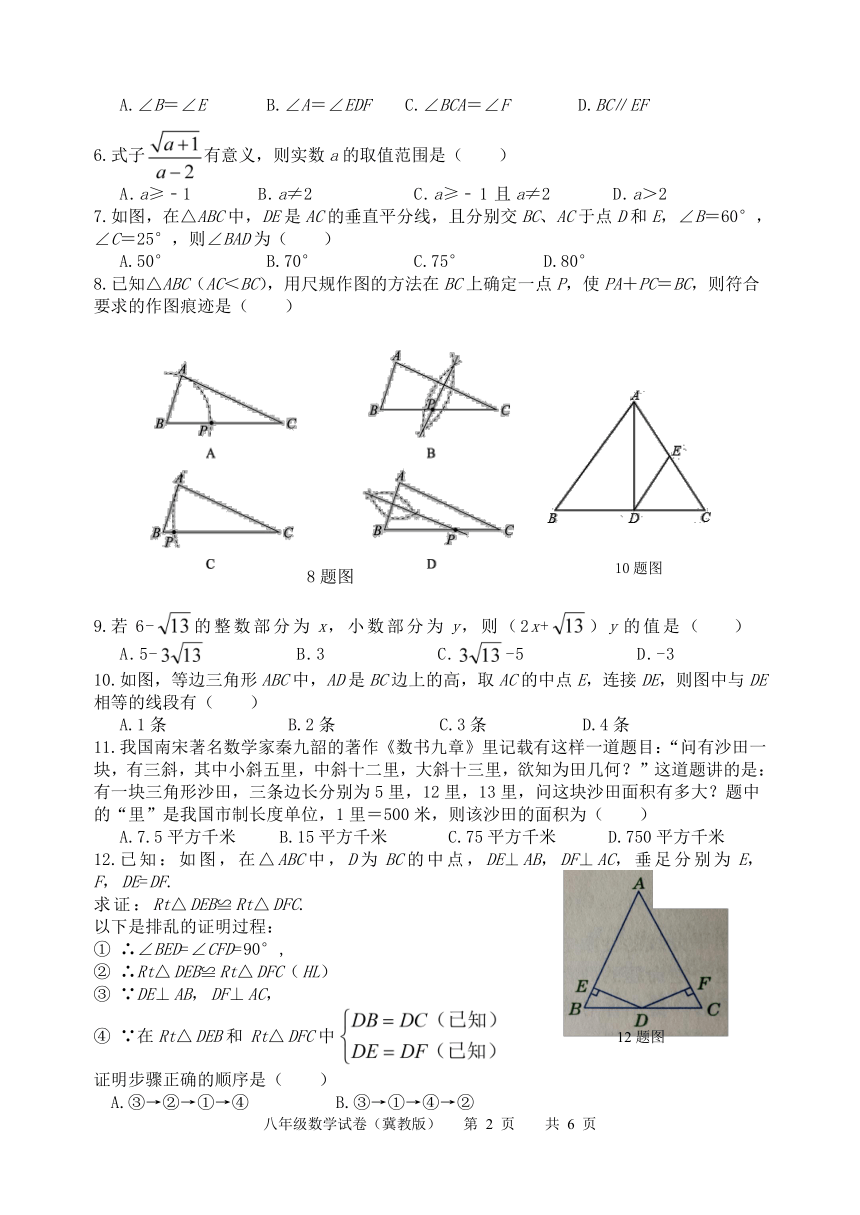
8.已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
9.若6-的整数部分为x,小数部分为y,则(2x+)y的值是( )
A.5- B.3 C.-5 D.-3
10.如图,等边三角形ABC中,AD是BC边上的高,取AC的中点E,连接DE,则图中与DE相等的线段有( )
A.1条 B.2条 C.3条 D.4条
11.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
12.已知:如图,在△ABC中,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,DE=DF.
求证:Rt△DEB≌Rt△DFC.
以下是排乱的证明过程:
① ∴∠BED=∠CFD=90°,
② ∴Rt△DEB≌Rt△DFC(HL)
③ ∵DE⊥AB,DF⊥AC,
④ ∵在Rt△DEB和Rt△DFC中
证明步骤正确的顺序是( )
A.③→②→①→④ B.③→①→④→②
C.①→②→④→③ D.①→④→③→②
二、填空题(本大题共8小题;每小题2分,共16分)
13.下列各式:① ② ③ ④是最简二次根式的是:
(填序号)
14.计算: .
15.我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农活动.老张在科技人员的指导下,改良核桃品种,喜获丰收,今年共获利润80249元,80249精确到万位的近似数是 .
16.在△ABC中,AB≠AC,若用反证法证明∠B≠∠C,应先假设 .
17.工人师傅在制作铝合金窗框时,为保证窗框的四个角都是直角,有时采用如下方法:如图,先量出框AB和BC的长,再量出点A和点C之间的距离,由此推断∠B是不是直角.这样做的依据是 .
18.如图,在△ABC中,BD、CE分别是边AC、 AB上的高,点F在BC上,BF=CF. BC=8cm,DE=3 cm.则△DEF的周长为 cm.
19.已知y=++4,则= .
20.如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后△CAP与△PQB全等.
三、解答题:(本大题共6个小题;共60分)
21.(本题满分7分)
22.(本题满分9分)
先化简,再求值:÷(a-1-),并从-1,0,1,2四个数中,选一个合适的数代入求值.
23.(本题满分9分)
作一个等腰三角形,使得底边长为线段a,底边上在高为线段b,要求保留作图痕迹(不要求写出作法)
24.(本题满分11分)
如图,将面积为2和3的两个正方形放置在数轴上,使得正方形的一个顶点和原点O重合,一条边恰好落在数轴正方向上,其另一个顶点分别为数轴上的点A和点B.
(1)点A和点B在数轴上对应的数分别是哪两个数?
(2)线段AB的长是多少?
(3)若将线段AB沿x轴向左平移4个单位,得到线段,则点,点在数轴上对应的数分别是哪两个数?并求出这两个数的乘积是多少?
25.(本题满分12分)
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
26.(本题满分12分)
已知:如图,在△ABC中,AD,BE分别是边BC,AC上的高,AD,BE相交于点F,AD=BD.
(1)求证:△BDF≌△ADC;
(2)若∠BAC=,求∠DBF的度数;
(3)若点D,E分别是边BC,AC的中点,则△ABC是什么特殊的三角形?
[请直接写出你的猜想]
八年级数学(一)答案
选择题(本大题共12小题;每小题2分,共24分)
1~6 A C B C A C; 7~12 B D B D A B .
二、填空题(本大题共8小题;每小题2分,共16分)
13. ②③; 14. ; 15. 8万; 16. ∠B=∠C ;
17. 勾股定理的逆定理; 18. 11; 19. 1; 20. 4.
三、解答题:(本大题共6个小题,共60分)
21.解:原式=…………………………………………………3分
= …………………………………………………………6分
=3 …………………………………………………………………………7分
22. 解:原式=÷……………………………………………………2分
=·……………………………………………………………4分
=. ……………………………………………………………………6分
在所给四个数中,当a=-1,0,2时,原式均无意义,
所以只能取a=1.…………………………………………………………………7分
当a=1时,原式==-1.……………………………………………………9分
23. 解:如图: ……………………………………………………………………………8分
所以△ABC就是所求作的三角形. …………………………………………………9分
24. 解:(1),; ……………………………………………………………2分
(2)-; ……………………………………………………………………4分
(3),, …………………………………………………………8分
………………………………………………………9分
= …………………………………………10分
= …………………………………………………11分
25. 解:设台式电脑的单价为x万元,则笔记本电脑的单价为1.5x万元, …………2分
由题意,得=120. …………………………………………………6分
解得x=0.24. ……………………………………………………………………8分
经检验,x=0.24为原方程的解,且符合题意.………………………………10分
1.5x=1.5×0.24=0.36. …………………………………………………………11分
答:台式电脑的单价为0.24万元,笔记本电脑的单价为0.36万元.……………12分
26. 解:(1)证明:∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°, ………………………………………………1分
∵∠C=∠C,
∴∠DBF=∠DAC. ……………………………………………………2分
在△BDF和△ADC中,
, ……………………………………………4分
∴△BDF≌△ADC(ASA). ……………………………………………5分
(2)∵AD=BD,AD⊥BC,
∴∠BAD=∠ABD=45°, …………………………………………………6分
∵∠BAC=∠BAD+∠DAC=,
∴∠DAC==, ………………………………………………8分
由(1)可知,∠DBF=∠DAC,
∴∠DBF=. …………………………………………………………10分
(3)△ABC是等边三角形. ……………………………………………………12分
检测八年级数学试题
考生注意:1.本卷共6页,总分100分,考试时间90分钟。
2.答题前请将密封线左侧的项目填写清楚。
3.答案请用蓝、黑色钢笔或圆珠笔填写。
题号
一
二
三
总分
21
22
23
24
25
26
得分
一、选择题(本大题共12个小题;每小题2分,共24分.在每小题给出的四个选项中只有一项是符合题意,请将正确答案的序号填在题中的括号内)
1.8的相反数的立方根是 ( )
A.-2 B. C. 2 D.-
2.悬针篆文具有较高的历史意义和研究价值,下面四个悬针篆文文字明显不是轴对称图形的是 ( )
3.如图,BD平分∠ABC,AD∥BC,则下列结论正确的是 ( )
A.BC=BD B.AB=AD C.DB=DC D.AD=DC
4.下列各式的计算中,正确的是( )
A.=× B.
C.=×=5 D.3=
5.如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
A.∠B=∠E B.∠A=∠EDF C.∠BCA=∠F D.BC∥EF
6.式子有意义,则实数a的取值范围是( )
A.a≥﹣1 B.a≠2 C.a≥﹣1且a≠2 D.a>2
7.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
8.已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
9.若6-的整数部分为x,小数部分为y,则(2x+)y的值是( )
A.5- B.3 C.-5 D.-3
10.如图,等边三角形ABC中,AD是BC边上的高,取AC的中点E,连接DE,则图中与DE相等的线段有( )
A.1条 B.2条 C.3条 D.4条
11.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
12.已知:如图,在△ABC中,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,DE=DF.
求证:Rt△DEB≌Rt△DFC.
以下是排乱的证明过程:
① ∴∠BED=∠CFD=90°,
② ∴Rt△DEB≌Rt△DFC(HL)
③ ∵DE⊥AB,DF⊥AC,
④ ∵在Rt△DEB和Rt△DFC中
证明步骤正确的顺序是( )
A.③→②→①→④ B.③→①→④→②
C.①→②→④→③ D.①→④→③→②
二、填空题(本大题共8小题;每小题2分,共16分)
13.下列各式:① ② ③ ④是最简二次根式的是:
(填序号)
14.计算: .
15.我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农活动.老张在科技人员的指导下,改良核桃品种,喜获丰收,今年共获利润80249元,80249精确到万位的近似数是 .
16.在△ABC中,AB≠AC,若用反证法证明∠B≠∠C,应先假设 .
17.工人师傅在制作铝合金窗框时,为保证窗框的四个角都是直角,有时采用如下方法:如图,先量出框AB和BC的长,再量出点A和点C之间的距离,由此推断∠B是不是直角.这样做的依据是 .
18.如图,在△ABC中,BD、CE分别是边AC、 AB上的高,点F在BC上,BF=CF. BC=8cm,DE=3 cm.则△DEF的周长为 cm.
19.已知y=++4,则= .
20.如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后△CAP与△PQB全等.
三、解答题:(本大题共6个小题;共60分)
21.(本题满分7分)
22.(本题满分9分)
先化简,再求值:÷(a-1-),并从-1,0,1,2四个数中,选一个合适的数代入求值.
23.(本题满分9分)
作一个等腰三角形,使得底边长为线段a,底边上在高为线段b,要求保留作图痕迹(不要求写出作法)
24.(本题满分11分)
如图,将面积为2和3的两个正方形放置在数轴上,使得正方形的一个顶点和原点O重合,一条边恰好落在数轴正方向上,其另一个顶点分别为数轴上的点A和点B.
(1)点A和点B在数轴上对应的数分别是哪两个数?
(2)线段AB的长是多少?
(3)若将线段AB沿x轴向左平移4个单位,得到线段,则点,点在数轴上对应的数分别是哪两个数?并求出这两个数的乘积是多少?
25.(本题满分12分)
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
26.(本题满分12分)
已知:如图,在△ABC中,AD,BE分别是边BC,AC上的高,AD,BE相交于点F,AD=BD.
(1)求证:△BDF≌△ADC;
(2)若∠BAC=,求∠DBF的度数;
(3)若点D,E分别是边BC,AC的中点,则△ABC是什么特殊的三角形?
[请直接写出你的猜想]
八年级数学(一)答案
选择题(本大题共12小题;每小题2分,共24分)
1~6 A C B C A C; 7~12 B D B D A B .
二、填空题(本大题共8小题;每小题2分,共16分)
13. ②③; 14. ; 15. 8万; 16. ∠B=∠C ;
17. 勾股定理的逆定理; 18. 11; 19. 1; 20. 4.
三、解答题:(本大题共6个小题,共60分)
21.解:原式=…………………………………………………3分
= …………………………………………………………6分
=3 …………………………………………………………………………7分
22. 解:原式=÷……………………………………………………2分
=·……………………………………………………………4分
=. ……………………………………………………………………6分
在所给四个数中,当a=-1,0,2时,原式均无意义,
所以只能取a=1.…………………………………………………………………7分
当a=1时,原式==-1.……………………………………………………9分
23. 解:如图: ……………………………………………………………………………8分
所以△ABC就是所求作的三角形. …………………………………………………9分
24. 解:(1),; ……………………………………………………………2分
(2)-; ……………………………………………………………………4分
(3),, …………………………………………………………8分
………………………………………………………9分
= …………………………………………10分
= …………………………………………………11分
25. 解:设台式电脑的单价为x万元,则笔记本电脑的单价为1.5x万元, …………2分
由题意,得=120. …………………………………………………6分
解得x=0.24. ……………………………………………………………………8分
经检验,x=0.24为原方程的解,且符合题意.………………………………10分
1.5x=1.5×0.24=0.36. …………………………………………………………11分
答:台式电脑的单价为0.24万元,笔记本电脑的单价为0.36万元.……………12分
26. 解:(1)证明:∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°, ………………………………………………1分
∵∠C=∠C,
∴∠DBF=∠DAC. ……………………………………………………2分
在△BDF和△ADC中,
, ……………………………………………4分
∴△BDF≌△ADC(ASA). ……………………………………………5分
(2)∵AD=BD,AD⊥BC,
∴∠BAD=∠ABD=45°, …………………………………………………6分
∵∠BAC=∠BAD+∠DAC=,
∴∠DAC==, ………………………………………………8分
由(1)可知,∠DBF=∠DAC,
∴∠DBF=. …………………………………………………………10分
(3)△ABC是等边三角形. ……………………………………………………12分
同课章节目录
