人教版九年级上册数学 24.2.2切线的性质与判定 课件(19张ppt)
文档属性
| 名称 | 人教版九年级上册数学 24.2.2切线的性质与判定 课件(19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-20 07:53:37 | ||
图片预览



文档简介
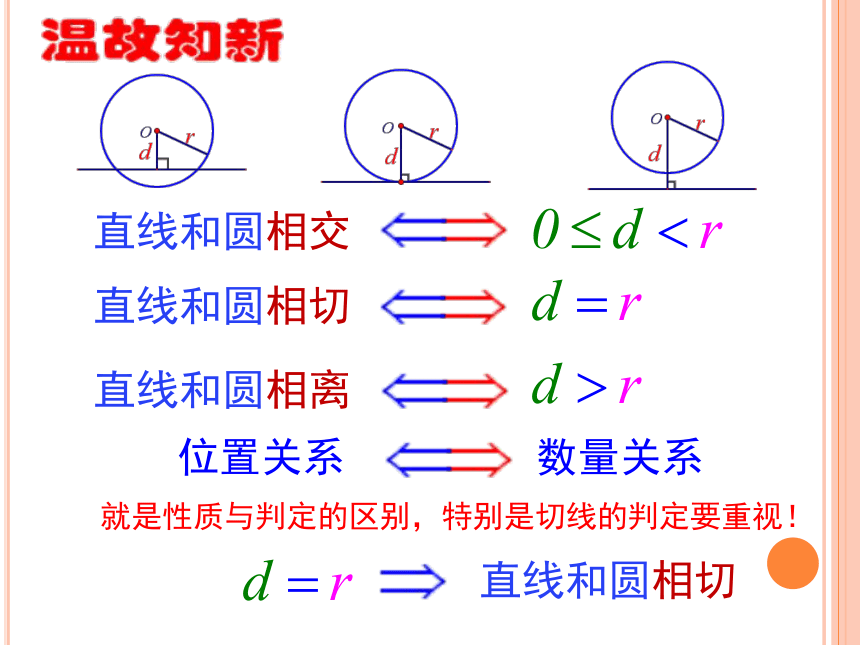
课件19张PPT。课题第二十四章24.2.2.(2) 切线的性质与判定温故直线和圆相交直线和圆相切直线和圆相离位置关系数量关系就是性质与判定的区别,特别是切线的判定要重视!直线和圆相切1.判定一条直线是否是圆的切线并会过圆上一点作圆的切线.2.理解并掌握圆的切线的判定定理及性质定理.(重点)4.经历探索知识过程,感受数学知识的价值和魅力,培养合作学习的意识和探索精神.学习目标:3.能运用圆的切线的判定定理和性质定理解决问题.(难点)4.经历探索知识过程,感受数学知识的价值和魅力,培养合作学习的意识和探索精神.目标新课引入 下雨天当你快速转动雨伞时飞出的水珠,在砂轮上打磨工件时飞出的火星中,让你感受到直线与圆的哪种位置关系?引入有一种“直线与圆相切”的感受.问题:
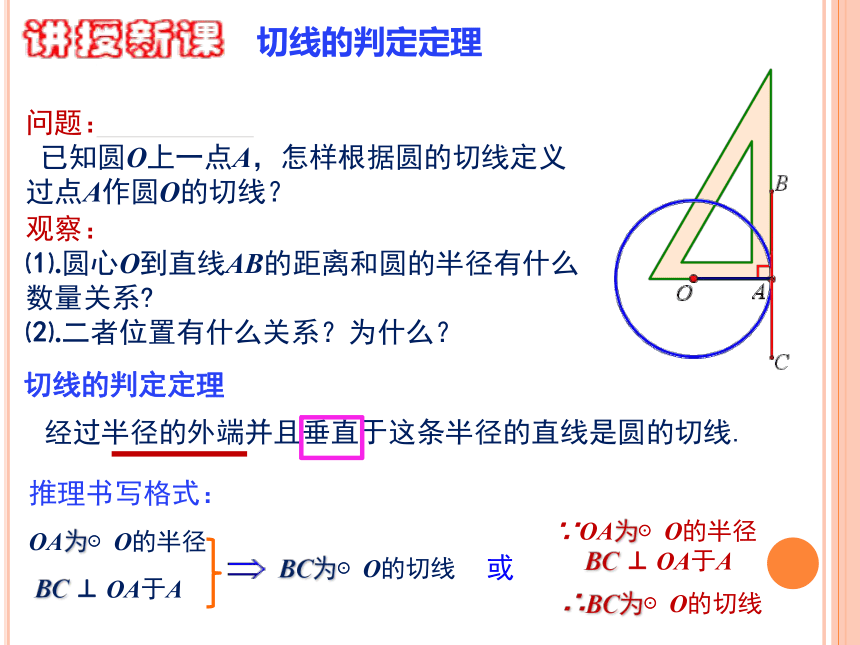
已知圆O上一点A,怎样根据圆的切线定义过点A作圆O的切线?观察:
⑴.圆心O到直线AB的距离和圆的半径有什么数量关系?
⑵.二者位置有什么关系?为什么?切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.切线的判定定理OA为⊙O的半径BC ⊥ OA于ABC为⊙O的切线推理书写格式:∵OA为⊙O的半径
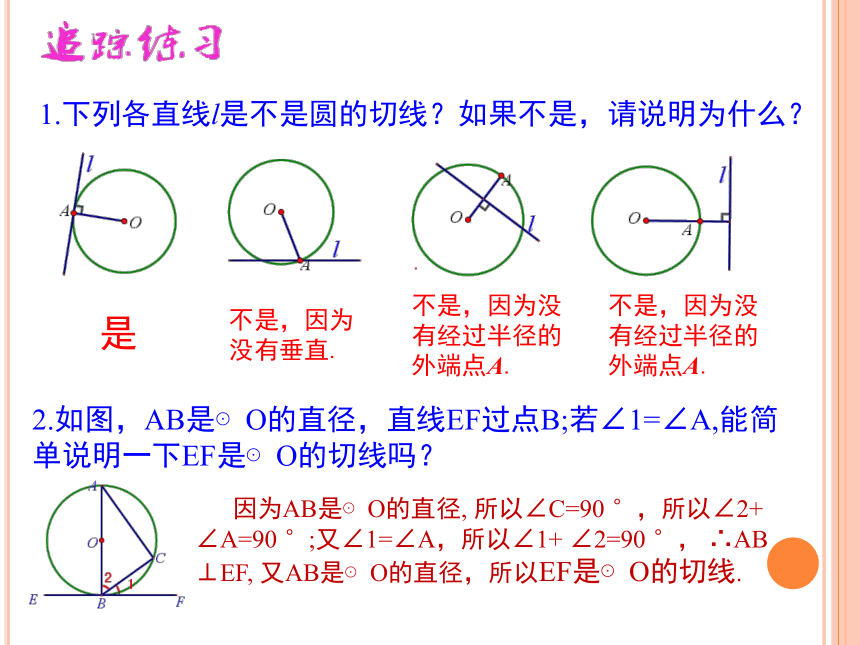
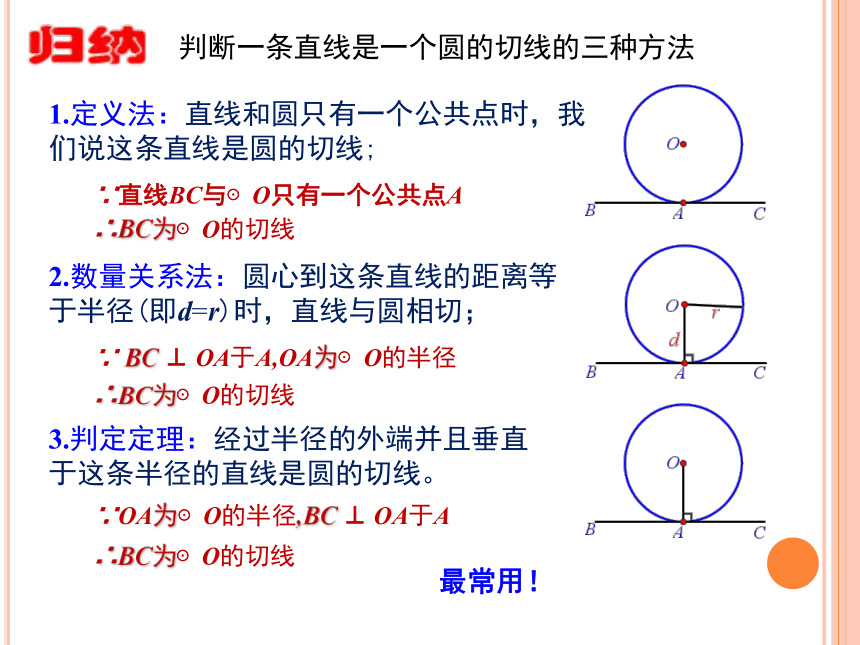
BC ⊥ OA于A∴BC为⊙O的切线或判定1.下列各直线l是不是圆的切线?如果不是,请说明为什么?不是,因为没有垂直.不是,因为没有经过半径的外端点A. 是不是,因为没有经过半径的外端点A.2.如图,AB是⊙O的直径,直线EF过点B;若∠1=∠A,能简单说明一下EF是⊙O的切线吗?追踪 因为AB是⊙O的直径, 所以∠C=90 °,所以∠2+ ∠A=90 °;又∠1=∠A,所以∠1+ ∠2=90 °, ∴AB ⊥EF, 又AB是⊙O的直径,所以EF是⊙O的切线.判断一条直线是一个圆的切线的三种方法1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;3.判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。归纳∵OA为⊙O的半径,BC ⊥ OA于A∴BC为⊙O的切线∵ BC ⊥ OA于A,OA为⊙O的半径 ∴BC为⊙O的切线∵直线BC与⊙O只有一个公共点A∴BC为⊙O的切线最常用!思考:如图,如果直线l是⊙O 的切线,点A为切点,那么OA与l垂直吗?切线的性质定理切线性质 圆的切线垂直于经过切点的半径. 性质∵直线l是⊙O的切线,A为切点∴直线l⊥OA证法1:反证法.证法2:构造法.⑴.假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,⑵.则OM∴ OC是等腰三角形OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径, ∴ AB是⊙O的切线.有公共点,连半径,证垂直!! 例2. 如图,△ABC 中,AB =AC ,O 是BC中点,⊙O 与AB 相切于E.求证:AC 是⊙O 的切线.分析:根据切线的判定定理,要证明AC是⊙O的切线,只要证明由点O向AC所作的垂线段OF是⊙O的半径就可以了,而OE是⊙O的半径,因此只需要证明OF=OE.典例2(续)证明:连接OE ,OA, 过O 作OF ⊥AC.∵⊙O 与AB 相切于E ,∴OE ⊥ AB.又∵△ABC 中AB =AC ,O 是BC 中点.∴AO 平分∠BAC∴OE =OF.∵OE 是⊙O 半径,OF =OE,OF ⊥ AC.∴AC 是⊙O 的切线.又∵OE ⊥AB ,OF⊥AC.无公共点,作垂直,证半径!!方法归纳例.如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB
求证:直线AB是⊙O的切线.例.如图,OA=OB=5,AB=8, ⊙O的直径为6.
求证:直线AB是⊙O的切线.?添辅助线方法归纳第一种情况第二种情况连接作垂直有公共点,连半径,证垂直!!无公共点,作垂直,证半径!!1.判断下列命题是否正确.
⑴.经过半径外端的直线是圆的切线. ( )
⑵.垂直于半径的直线是圆的切线. ( )
⑶.过直径的外端并且垂直于这条直径的直线是圆的切线. ( )
⑷.和圆只有一个公共点的直线是圆的切线. ( )
⑸.过直径一端点且垂直于直径的直线是圆的切线. ( )3.如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为 ( )
A.40° B.35° C.30° D.45°2.如图所示,A是⊙O上一点,且AO=5,PO=13,AP=12,则PA与⊙O的位置关系是 .巩固练习相切C4.如图,已知AB是⊙ O的切线,半径OC的延长线与AB相交于点B,且OC=BC.
⑴.求证:AC= OB;
⑵.求∠B的度数.5.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E.
求证:PE是⊙O的切线.6.如图,⊙O的半径为8厘米,圆内的弦AB为 厘米,以O为圆心,4厘米为半径作小圆.
求证:小圆与直线AB相切。4、5、6题根据课堂时间选做!巩固练习(续)例1.Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是边BC的中点,连接DE.
求证:直线DE是⊙O的切线.略证:连接OD、BD.∵AB是⊙O直径∴∠ADB=90°∴∠CDB=90°又∵E为边BC的中点∴∴DE=CE∴∠1=∠C∵OA=OD∴∠2=∠A∵∠ABC=90°∴∠A+∠C=90°∴∠1+∠2=90°∴∠ODE=90°又∵OD是⊙O的半径∴直线DE是⊙O的切线记住哟!“有公共点,连半径,证垂直.”能力提升例1例2.已知:△ABC内接于⊙O,过点A作直线EF.
⑴.如图1,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出两种情况):
① ._________ ;② ._____________ .
⑵.如图2,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.BA⊥EF∠CAE=∠B证明:
连接AO并延长交⊙O于D,连接CD,则AD为⊙O的直径.例2∴ ∠D+ ∠DAC=90 °
∵ ∠D与∠B同对
∴ ∠D= ∠B,
又∵ ∠CAE= ∠B,
∴ ∠D= ∠CAE,
∴ ∠DAC+ ∠EAC=90°
∴EF是⊙O的切线.∴EF是⊙O的切线.牛刀小试(1).可证明∠1+∠2=∠3+∠B=90°;(2).可设RQ=x,则在Rt△OQR中有:22+x2=(x+1)2 .比如:若①②推出③可连接OD.然后证明ODE=∠DEC=90°.谈谈你的收获!谈谈收获!切线的
判定方法定义法数量关系法判定定理1个公共点,则相切d=r,则相切经过半径的外端并且垂直于这条半径的直线是圆的切线切线的
性质证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.有1个公共点d=r性质定理圆的切线垂直于经过切点的半径 有切线时常用辅助线添加方法:
见切线,连切点,得垂直.作业布置书面作业:再见!1.书上98页练习题,书上101页4、5题;
2.《探究丛书》107页14、15题.
课外探究:《实践与探究》108页 的“拓展与探究”
已知圆O上一点A,怎样根据圆的切线定义过点A作圆O的切线?观察:
⑴.圆心O到直线AB的距离和圆的半径有什么数量关系?
⑵.二者位置有什么关系?为什么?切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.切线的判定定理OA为⊙O的半径BC ⊥ OA于ABC为⊙O的切线推理书写格式:∵OA为⊙O的半径
BC ⊥ OA于A∴BC为⊙O的切线或判定1.下列各直线l是不是圆的切线?如果不是,请说明为什么?不是,因为没有垂直.不是,因为没有经过半径的外端点A. 是不是,因为没有经过半径的外端点A.2.如图,AB是⊙O的直径,直线EF过点B;若∠1=∠A,能简单说明一下EF是⊙O的切线吗?追踪 因为AB是⊙O的直径, 所以∠C=90 °,所以∠2+ ∠A=90 °;又∠1=∠A,所以∠1+ ∠2=90 °, ∴AB ⊥EF, 又AB是⊙O的直径,所以EF是⊙O的切线.判断一条直线是一个圆的切线的三种方法1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;3.判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。归纳∵OA为⊙O的半径,BC ⊥ OA于A∴BC为⊙O的切线∵ BC ⊥ OA于A,OA为⊙O的半径 ∴BC为⊙O的切线∵直线BC与⊙O只有一个公共点A∴BC为⊙O的切线最常用!思考:如图,如果直线l是⊙O 的切线,点A为切点,那么OA与l垂直吗?切线的性质定理切线性质 圆的切线垂直于经过切点的半径. 性质∵直线l是⊙O的切线,A为切点∴直线l⊥OA证法1:反证法.证法2:构造法.⑴.假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,⑵.则OM
∴ AB⊥OC.
∵ OC是⊙O的半径, ∴ AB是⊙O的切线.有公共点,连半径,证垂直!! 例2. 如图,△ABC 中,AB =AC ,O 是BC中点,⊙O 与AB 相切于E.求证:AC 是⊙O 的切线.分析:根据切线的判定定理,要证明AC是⊙O的切线,只要证明由点O向AC所作的垂线段OF是⊙O的半径就可以了,而OE是⊙O的半径,因此只需要证明OF=OE.典例2(续)证明:连接OE ,OA, 过O 作OF ⊥AC.∵⊙O 与AB 相切于E ,∴OE ⊥ AB.又∵△ABC 中AB =AC ,O 是BC 中点.∴AO 平分∠BAC∴OE =OF.∵OE 是⊙O 半径,OF =OE,OF ⊥ AC.∴AC 是⊙O 的切线.又∵OE ⊥AB ,OF⊥AC.无公共点,作垂直,证半径!!方法归纳例.如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB
求证:直线AB是⊙O的切线.例.如图,OA=OB=5,AB=8, ⊙O的直径为6.
求证:直线AB是⊙O的切线.?添辅助线方法归纳第一种情况第二种情况连接作垂直有公共点,连半径,证垂直!!无公共点,作垂直,证半径!!1.判断下列命题是否正确.
⑴.经过半径外端的直线是圆的切线. ( )
⑵.垂直于半径的直线是圆的切线. ( )
⑶.过直径的外端并且垂直于这条直径的直线是圆的切线. ( )
⑷.和圆只有一个公共点的直线是圆的切线. ( )
⑸.过直径一端点且垂直于直径的直线是圆的切线. ( )3.如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为 ( )
A.40° B.35° C.30° D.45°2.如图所示,A是⊙O上一点,且AO=5,PO=13,AP=12,则PA与⊙O的位置关系是 .巩固练习相切C4.如图,已知AB是⊙ O的切线,半径OC的延长线与AB相交于点B,且OC=BC.
⑴.求证:AC= OB;
⑵.求∠B的度数.5.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E.
求证:PE是⊙O的切线.6.如图,⊙O的半径为8厘米,圆内的弦AB为 厘米,以O为圆心,4厘米为半径作小圆.
求证:小圆与直线AB相切。4、5、6题根据课堂时间选做!巩固练习(续)例1.Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是边BC的中点,连接DE.
求证:直线DE是⊙O的切线.略证:连接OD、BD.∵AB是⊙O直径∴∠ADB=90°∴∠CDB=90°又∵E为边BC的中点∴∴DE=CE∴∠1=∠C∵OA=OD∴∠2=∠A∵∠ABC=90°∴∠A+∠C=90°∴∠1+∠2=90°∴∠ODE=90°又∵OD是⊙O的半径∴直线DE是⊙O的切线记住哟!“有公共点,连半径,证垂直.”能力提升例1例2.已知:△ABC内接于⊙O,过点A作直线EF.
⑴.如图1,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出两种情况):
① ._________ ;② ._____________ .
⑵.如图2,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.BA⊥EF∠CAE=∠B证明:
连接AO并延长交⊙O于D,连接CD,则AD为⊙O的直径.例2∴ ∠D+ ∠DAC=90 °
∵ ∠D与∠B同对
∴ ∠D= ∠B,
又∵ ∠CAE= ∠B,
∴ ∠D= ∠CAE,
∴ ∠DAC+ ∠EAC=90°
∴EF是⊙O的切线.∴EF是⊙O的切线.牛刀小试(1).可证明∠1+∠2=∠3+∠B=90°;(2).可设RQ=x,则在Rt△OQR中有:22+x2=(x+1)2 .比如:若①②推出③可连接OD.然后证明ODE=∠DEC=90°.谈谈你的收获!谈谈收获!切线的
判定方法定义法数量关系法判定定理1个公共点,则相切d=r,则相切经过半径的外端并且垂直于这条半径的直线是圆的切线切线的
性质证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.有1个公共点d=r性质定理圆的切线垂直于经过切点的半径 有切线时常用辅助线添加方法:
见切线,连切点,得垂直.作业布置书面作业:再见!1.书上98页练习题,书上101页4、5题;
2.《探究丛书》107页14、15题.
课外探究:《实践与探究》108页 的“拓展与探究”
同课章节目录
