高中数学第二章平面解析几何初步2.3.4圆与圆的位置关系课件新人教B版必修2
文档属性
| 名称 | 高中数学第二章平面解析几何初步2.3.4圆与圆的位置关系课件新人教B版必修2 |  | |
| 格式 | zip | ||
| 文件大小 | 647.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-19 21:45:01 | ||
图片预览









文档简介
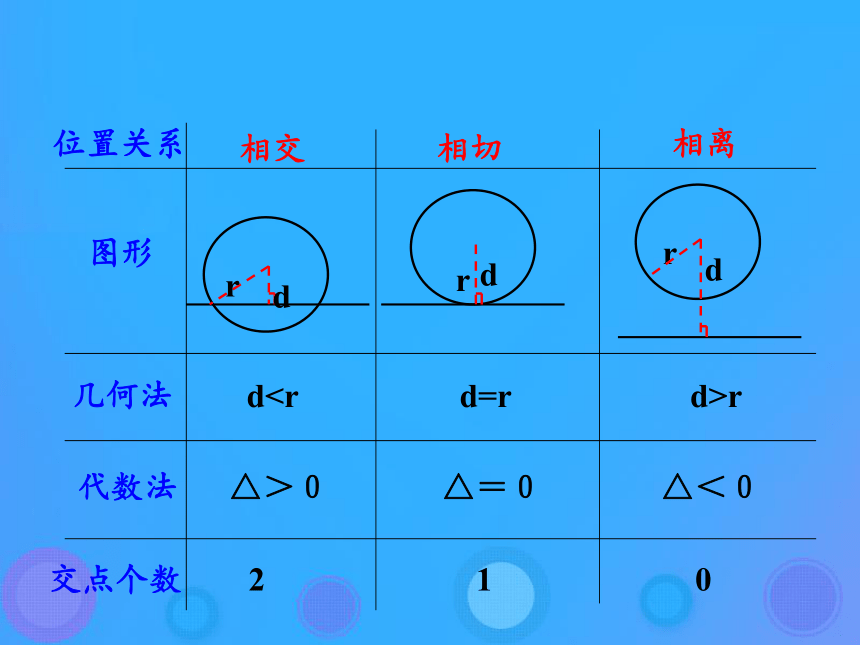
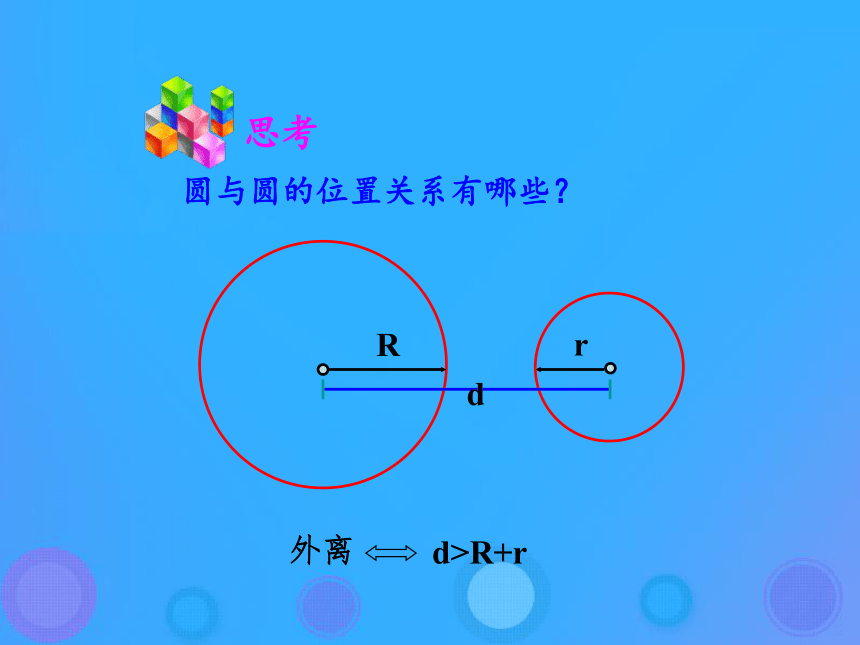
课件39张PPT。2.3.4 圆与圆的位置关系直线与圆的位置关系的判定圆与圆的位置关系有哪些?思考随着圆心距的增加,两圆的关系发生变化.思考 已知两圆C1:x2+y2+D1x+E1y+F1=0和C2:x2+y2+D2x+E2y+F2=0,如何根据圆的方程判断圆与圆的位置关系? 1.将两圆的方程化为标准方程;2.求两圆的圆心坐标和半径R、r;3.求两圆的圆心距d; 4.比较d与R-r,R+r的大小关系.若d<|R-r|,则两圆内含;
若d=|R-r|,则两圆内切;
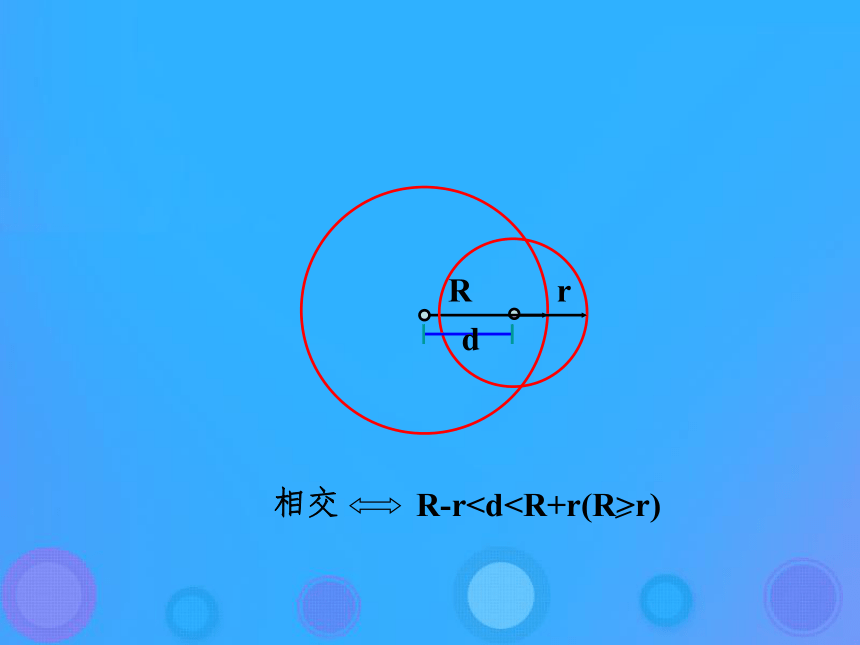
若|R-r|<d<R+r,则两圆相交;
若d=R+r,则两圆外切;
若d>R+r,则两圆外离. 能否根据两个圆的公共点个数判断两圆的位置关系? 思考利用两个圆的方程组成方程组的实数解的个数:Δ<0Δ>0Δ=0Δ<0圆与圆的位置关系圆与圆的位置关 已知圆C1:x2+y2-6x+8y=0和圆C2:x2+y2+2x-3=0,试判断圆C1与圆C2的位置关系.例1方法一方法二将C1的方程化成标准方程,得将C2的方程化成标准方程,得圆心坐标(3,-4),半径为5.圆心坐标(-1,0),半径为2.圆C1与C2的连心线的长为:圆C1与圆C2的半径长之和为:r1+r2=5+2=7圆C1与圆C2的半径长之差为:r1-r2=5-2=3因为所以两圆相交.例2.a何值时,两圆:
C1:x2+y2-2ax+4y+a2-5=0 C2:x2+y2+2x-2ay+a2-3=0,
(1) 相切;(2)相交;(3)相离 .解:小试牛刀(一)
2.两圆
相切,试确定常数 的值。
1.判断下列两个圆的位置关系:3.圆系与圆系方程
具有某种共同性质的圆的集合,称为_______.
(1)同心圆系(x-x0)2+(y-y0)2=r2,x0,y0为常数,r为参数.
(2)圆心共线且半径相等圆系(x-x0)2+(y-y0)2=r2,r为常数,圆心(x0,y0)在直线Ax+By+C=0上移动.
(3)过两已知圆x2+y2+D1x+E1y+F1=0,
的交点的圆系方程:
x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0,圆系即f1(x,y)+λf2(x,y)=0(λ≠-1).
当λ=-1时,变为(D1-D2)x+(E1-E2)y+F1-F2=0,表示过两圆的交点的直线(当两圆是同心圆时,此直线不存在),当两圆相交时,此直线为公共弦所在直线;当两圆相切时,此直线为两圆的公切线;当两圆相离时,此直线为与两圆连心线垂直的直线.
(4)过直线与圆交点的圆系方程
设直线l:Ax+By+C=0与圆C:x2+y2+Dx+Ey+F=0相交,则方程x2+y2+Dx+Ey+F+λ(Ax+By+C)=0表示过直线l与圆C的两个交点的圆系方程.法1.例题讲解法2..小试牛刀(二):2.已知圆:与圆:64. 求过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点,且面积最小的圆的方程.
解:设过直线2x+y+4=0和圆x2+y2+2x-4y+1=0交点的圆系方程为x2+y2+2x-4y+1+λ(2x+y+4)=0,
整理得x2+y2+2(1+λ)x-(4-λ)y+1+4λ=0.
要使圆的面积最小,即要求半径r最小.答案:判断两圆的位置关系的两种方法:1.根据圆心距与半径和之间的大小关系.若d<|R-r|,则两圆内含;
若d=|R-r|,则两圆内切;
若|R-r|<d<R+r,则两圆相交;
若d=R+r,则两圆外切;
若d>R+r,则两圆外离. 2.联立两圆方程,看截得解得个数.【解析】由题意,得
,故选B B1.判断下列两圆的位置关系.(2)圆A:x2+y2=1与圆B:x2+y2+6x-8y-24=0的位置关系是___________内切2 .已知两圆(x-3)2 + (y-2)2=25和(x-1)2+ (y-2)2=r2相内切,则半径r= ( )B(1)圆A:(x-3)2+(y+2)2=1与圆B:(x-7)2+(y-1)2=36的位置关系是___________内含3.两圆半径是方程 2x2-10x+3=0 的两个实数根 ,当两圆的圆心距等于 7 时,它们的位置关系是( )A. 相交 B. 外切 C. 内切 D. 外离 4.两圆半径之比为 1 : 2 ,已知这两个圆内切时的圆心距为5,那么这两圆相交时圆心距 d 的取值范围为( )A.d>5 B.5C.515 DB外离06.两个同心圆的位置关系是:_______.内含7.圆O1和圆O2的半径分别为R、r,圆心距为d,下列情况下圆O1和圆O2的位置关系怎样?(1)R=4 r=3 d=8外离(2)R=4 r=3 d=1内切(3)R=1 r=6 d=7外切(4)R=5 r=3 d=3相交(5)R=5 r=3 d=1内含5.把自行车的两个轮子看作两个圆,则它们的位置关系_______公共点______个.8.两圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径为_______.3或79.已知⊙O1、⊙O2的半径为r1、r2,如果r1=5,r2=3,且⊙O1、⊙O2相切,那么圆心距d=________.8或2C1 (-1,-4)C2(2,2)
交点坐标A(-1,1),B(3,1) 直线方程为
x+2y-1=0解:联立方程组,得xyAB 11.已知两圆外切,圆心距为15cm,一条外公切线的长为 ,求这两个圆的半径.分析:R + r = 15,R – r = 5
所以:R=10,r=5.C
若d=|R-r|,则两圆内切;
若|R-r|<d<R+r,则两圆相交;
若d=R+r,则两圆外切;
若d>R+r,则两圆外离. 能否根据两个圆的公共点个数判断两圆的位置关系? 思考利用两个圆的方程组成方程组的实数解的个数:Δ<0Δ>0Δ=0Δ<0圆与圆的位置关系圆与圆的位置关 已知圆C1:x2+y2-6x+8y=0和圆C2:x2+y2+2x-3=0,试判断圆C1与圆C2的位置关系.例1方法一方法二将C1的方程化成标准方程,得将C2的方程化成标准方程,得圆心坐标(3,-4),半径为5.圆心坐标(-1,0),半径为2.圆C1与C2的连心线的长为:圆C1与圆C2的半径长之和为:r1+r2=5+2=7圆C1与圆C2的半径长之差为:r1-r2=5-2=3因为所以两圆相交.例2.a何值时,两圆:
C1:x2+y2-2ax+4y+a2-5=0 C2:x2+y2+2x-2ay+a2-3=0,
(1) 相切;(2)相交;(3)相离 .解:小试牛刀(一)
2.两圆
相切,试确定常数 的值。
1.判断下列两个圆的位置关系:3.圆系与圆系方程
具有某种共同性质的圆的集合,称为_______.
(1)同心圆系(x-x0)2+(y-y0)2=r2,x0,y0为常数,r为参数.
(2)圆心共线且半径相等圆系(x-x0)2+(y-y0)2=r2,r为常数,圆心(x0,y0)在直线Ax+By+C=0上移动.
(3)过两已知圆x2+y2+D1x+E1y+F1=0,
的交点的圆系方程:
x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0,圆系即f1(x,y)+λf2(x,y)=0(λ≠-1).
当λ=-1时,变为(D1-D2)x+(E1-E2)y+F1-F2=0,表示过两圆的交点的直线(当两圆是同心圆时,此直线不存在),当两圆相交时,此直线为公共弦所在直线;当两圆相切时,此直线为两圆的公切线;当两圆相离时,此直线为与两圆连心线垂直的直线.
(4)过直线与圆交点的圆系方程
设直线l:Ax+By+C=0与圆C:x2+y2+Dx+Ey+F=0相交,则方程x2+y2+Dx+Ey+F+λ(Ax+By+C)=0表示过直线l与圆C的两个交点的圆系方程.法1.例题讲解法2..小试牛刀(二):2.已知圆:与圆:64. 求过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点,且面积最小的圆的方程.
解:设过直线2x+y+4=0和圆x2+y2+2x-4y+1=0交点的圆系方程为x2+y2+2x-4y+1+λ(2x+y+4)=0,
整理得x2+y2+2(1+λ)x-(4-λ)y+1+4λ=0.
要使圆的面积最小,即要求半径r最小.答案:判断两圆的位置关系的两种方法:1.根据圆心距与半径和之间的大小关系.若d<|R-r|,则两圆内含;
若d=|R-r|,则两圆内切;
若|R-r|<d<R+r,则两圆相交;
若d=R+r,则两圆外切;
若d>R+r,则两圆外离. 2.联立两圆方程,看截得解得个数.【解析】由题意,得
,故选B B1.判断下列两圆的位置关系.(2)圆A:x2+y2=1与圆B:x2+y2+6x-8y-24=0的位置关系是___________内切2 .已知两圆(x-3)2 + (y-2)2=25和(x-1)2+ (y-2)2=r2相内切,则半径r= ( )B(1)圆A:(x-3)2+(y+2)2=1与圆B:(x-7)2+(y-1)2=36的位置关系是___________内含3.两圆半径是方程 2x2-10x+3=0 的两个实数根 ,当两圆的圆心距等于 7 时,它们的位置关系是( )A. 相交 B. 外切 C. 内切 D. 外离 4.两圆半径之比为 1 : 2 ,已知这两个圆内切时的圆心距为5,那么这两圆相交时圆心距 d 的取值范围为( )A.d>5 B.5
交点坐标A(-1,1),B(3,1) 直线方程为
x+2y-1=0解:联立方程组,得xyAB 11.已知两圆外切,圆心距为15cm,一条外公切线的长为 ,求这两个圆的半径.分析:R + r = 15,R – r = 5
所以:R=10,r=5.C
