高中数学第二章平面解析几何初步2.4空间直角坐标系课件新人教B版必修2(36张PPT)
文档属性
| 名称 | 高中数学第二章平面解析几何初步2.4空间直角坐标系课件新人教B版必修2(36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-19 00:00:00 | ||
图片预览









文档简介
课件36张PPT。§2.4 空间直角坐标系 知识探究(一):空间直角坐标系 思考1:数轴上的点M的坐标用一个实数x表示,它是一维坐标;平面上的点M的坐标用一对有序实数(x,y)表示,它是二维坐标.设想:对于空间中的点的坐标,需要几个实数表示?
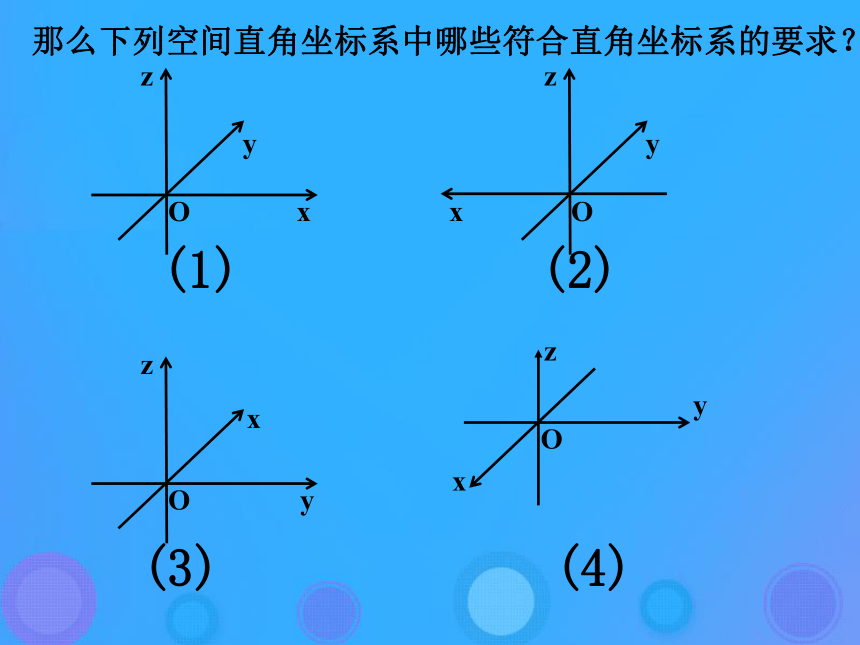
思考2:平面直角坐标系由两条互相垂直的数轴组成,设想:空间直角坐标系由几条数轴组成?其相对位置关系如何? 三条交于一点且两两互相垂直的数轴 思考3:在空间中,取三条交于一点且两两互相垂直的数轴:x轴、y轴、z轴,组成空间直角坐标系Oxyz,在平面上如何画空间直角坐标系? ∠xOy=135°∠yOz=90° 思考4:在空间直角坐标系中,对三条数轴的方向作如下约定:伸出右手,拇指指向为x轴正方向,食指指向为y轴正方向,中指指向为z轴正方向,并称这样的坐标系为右手直角坐标系.xyzO(1)(2)(3)(4)那么下列空间直角坐标系中哪些符合直角坐标系的要求?
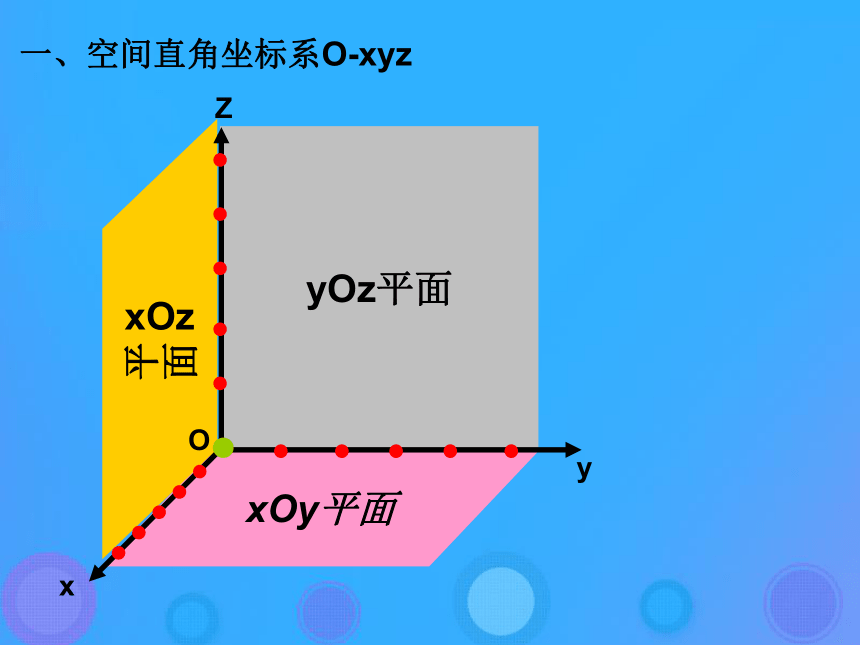
xOy平面yOz平面xOz
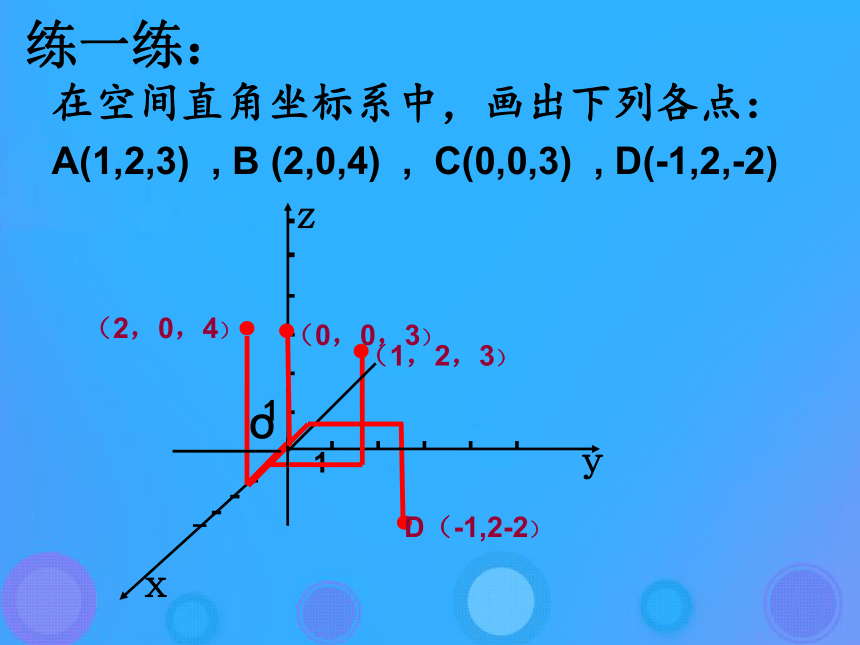
平面O一、空间直角坐标系O-xyz xzyoxyz(x,y,z)A点A的坐标A(3,4,3)思考5:如何确定空间直角坐标系中点的坐标1、判断正误:(1)在空间直角坐标系中,x轴,y轴,z轴是有向直线。(2)将空间坐标系画在纸上时,各轴单位长是相等的。(3)在空间任意一点的空间坐标都是唯一的。(4)在空间直角坐标系中,点的坐标由它在各轴上的射影唯一确定。巩固练习1(√)(√)(X)(X)例1 在空间直角坐标系中,作出点(5,4,6)O546O练一练:在空间直角坐标系中,画出下列各点:
A(1,2,3) , B (2,0,4) , C(0,0,3) , D(-1,2,-2) 例2.现有长方体ABCD-A'B'C'D'如图,其中AB=12,AD=8,AA'=5 ,试建立适当的空间直角坐标系,并写出该长方体各定点的坐标。AB'DCBD'C'A'1285ADCBD'C'A'特殊位置的点的坐标原点(0,0,0)
x轴上的点(x,0,0)
y轴上的点(0,y,0)
z轴上的点(0,0,z)
xOy平面上的点(x,y,0)
yOz平面上的点(0,y,z)
zOx平面上的点(x,0,z)(0,0,0)(12,0,0)(0,0,5)(0,8,0)(12,8,0)(12,0,5)(0,8,5)(12,8,5)BACKB'ADCBD'C'A'1258二、对称点xyOx0y0(x0,y0)P(x0 , -y0)P1横坐标不变,
纵坐标相反。(-x0 ,y0)P2横坐标相反,
纵坐标不变。P3横坐标相反,
纵坐标相反。-y0-x0(-x0 , -y0)思考6:设点M的坐标为(x,y,z)那么点M关于x轴、y轴、z轴及原点对称的点的坐标分别是什么?M(x,y,z)N(x,-y,-z)一般的P(x , y , z) 关于:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;
关于谁对称谁不变1、关于轴对称一般的P(x , y , z) 关于:
(1)xoy平面对称的点P1为__________;
(2)yoz平面对称的点P2为__________;
(3)zox平面对称的点P3为__________;关于谁对称谁不变(x,y,-z)(-x,y, z)(x, -y, z)2、关于坐标平面对称3、关于坐标原点对称?P(x , y , z)关于坐标原点对称为(-x, -y, -z)思考6:设点M的坐标为(x,y,z)那么点M关于xoy平面、yoz平面、xoz平面的对称点坐标是什么?M(x,y,z)N(x,y,-z)在空间直角坐标系中,点P(1,2,3)关于y轴的对称点是__________________
在空间直角坐标系中,点P(1,2,3)关于x轴的对称点是__________________
在空间直角坐标系中,点P(1,2,3)关于z轴的对称点是__________________(-1,2,-3)(1,-2,-3)(-1,-2,3)巩固练习2在空间直角坐标系中,点P(1,2,3)关于xOy面的对称点是_________________
在空间直角坐标系中,点P(1,2,3)关于yOz面的对称点是_________________
在空间直角坐标系中,点P(1,2,3)关于zOx面的对称点是_________________(1,2,-3)(-1,2,3)(1,-2,3)巩固练习2思考7:在空间直角坐标系Oxyz中,三个坐标平面将空间分成几个部分?每一部分的坐标有何不同?八个卦限中点的坐标符号分别为:
I: ( + ,+ ,+ );
II: ( - ,+ ,+ );
III: ( - ,- ,+ );
IV: ( + ,- ,+ );
V: ( + ,+ ,- );
VI: ( - ,+ ,- );
VII:( - ,- ,- );
VIII:( + ,- ,- );2、在空间直角坐标系中,点 ,过点P作平面yoz的垂线则垂足Q的坐标是?3、点P(-3,1,-2)沿x轴负方向平移2个单位,沿y轴正方向平移1个单位,向z轴正方向平移2个单位得到点P',则点P'的坐标是多少?P(-5,2,0)思考8:设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?思考9:设点A(x1,y1,z1),
点B(x2,y2,z2),则AB的距离如何?空间任意两点间的距离.|P1Q1|=|x1-x2|;|Q1R1|=|y1-y2|;|R1P2|=|z1-z2||P1P2|2=|P1Q1||2+|Q1R1|2+|R1P2|2 已知A(1,-2,11),B(4,2,3),C(6,-1,4),求证其连线组成的三角形为直角三角形。利用两点间距离公式,由从而,根据勾股定理,结论得证。例4 在四面体P-ABCA中,PA、PB、PC两两垂直,设PA=PB=PC=a,求点P到平面ABC的距离。例5ABC 根据题意,建立如图所示的坐标系,则P(0,0,0),A(a,0,0),B(0,a,0),C(0,0,a) 过点P作PH⊥平面ABC,交平面ABC于H,则PH的长即为点P到平面ABC的距离。∵PA=PB=PC,∴H为 的外心,又∵ 为正三角形,∴点P到平面ABC的距离是∴H为 的重心,可得点H的坐标为1.在空间直角坐标系中,已知点P(x,y,z),给出下列4条叙述:
①点P关于x轴的对称点的坐标是(x,-y,z)
②点P关于yOz平面的对称点的坐标是(x,-y,-z)
③点P关于y轴的对称点的坐标是(x,-y,z)
④点P关于原点的对称点的坐标是(-x,-y,-z)
其中正确的个数是(????)
A.3 B.2 C.1 D.0C2.点B是点A(1,2,3)在坐标平面yOz内的射影,则OB等于(????)BA. B. C. D.3.如图,长方体ABCD-A’B’C’D’中,|AD|=3,|AB|=5,|AA’|=3,设E为DB’的中点,F为BC‘的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,A’,B’,C’,D’,E,F各点的坐标。小结1、空间直角坐标系的建立。 2、空间中的点。3、对称点 。4、特殊位置的点的坐标谢谢!
思考2:平面直角坐标系由两条互相垂直的数轴组成,设想:空间直角坐标系由几条数轴组成?其相对位置关系如何? 三条交于一点且两两互相垂直的数轴 思考3:在空间中,取三条交于一点且两两互相垂直的数轴:x轴、y轴、z轴,组成空间直角坐标系Oxyz,在平面上如何画空间直角坐标系? ∠xOy=135°∠yOz=90° 思考4:在空间直角坐标系中,对三条数轴的方向作如下约定:伸出右手,拇指指向为x轴正方向,食指指向为y轴正方向,中指指向为z轴正方向,并称这样的坐标系为右手直角坐标系.xyzO(1)(2)(3)(4)那么下列空间直角坐标系中哪些符合直角坐标系的要求?
xOy平面yOz平面xOz
平面O一、空间直角坐标系O-xyz xzyoxyz(x,y,z)A点A的坐标A(3,4,3)思考5:如何确定空间直角坐标系中点的坐标1、判断正误:(1)在空间直角坐标系中,x轴,y轴,z轴是有向直线。(2)将空间坐标系画在纸上时,各轴单位长是相等的。(3)在空间任意一点的空间坐标都是唯一的。(4)在空间直角坐标系中,点的坐标由它在各轴上的射影唯一确定。巩固练习1(√)(√)(X)(X)例1 在空间直角坐标系中,作出点(5,4,6)O546O练一练:在空间直角坐标系中,画出下列各点:
A(1,2,3) , B (2,0,4) , C(0,0,3) , D(-1,2,-2) 例2.现有长方体ABCD-A'B'C'D'如图,其中AB=12,AD=8,AA'=5 ,试建立适当的空间直角坐标系,并写出该长方体各定点的坐标。AB'DCBD'C'A'1285ADCBD'C'A'特殊位置的点的坐标原点(0,0,0)
x轴上的点(x,0,0)
y轴上的点(0,y,0)
z轴上的点(0,0,z)
xOy平面上的点(x,y,0)
yOz平面上的点(0,y,z)
zOx平面上的点(x,0,z)(0,0,0)(12,0,0)(0,0,5)(0,8,0)(12,8,0)(12,0,5)(0,8,5)(12,8,5)BACKB'ADCBD'C'A'1258二、对称点xyOx0y0(x0,y0)P(x0 , -y0)P1横坐标不变,
纵坐标相反。(-x0 ,y0)P2横坐标相反,
纵坐标不变。P3横坐标相反,
纵坐标相反。-y0-x0(-x0 , -y0)思考6:设点M的坐标为(x,y,z)那么点M关于x轴、y轴、z轴及原点对称的点的坐标分别是什么?M(x,y,z)N(x,-y,-z)一般的P(x , y , z) 关于:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;
关于谁对称谁不变1、关于轴对称一般的P(x , y , z) 关于:
(1)xoy平面对称的点P1为__________;
(2)yoz平面对称的点P2为__________;
(3)zox平面对称的点P3为__________;关于谁对称谁不变(x,y,-z)(-x,y, z)(x, -y, z)2、关于坐标平面对称3、关于坐标原点对称?P(x , y , z)关于坐标原点对称为(-x, -y, -z)思考6:设点M的坐标为(x,y,z)那么点M关于xoy平面、yoz平面、xoz平面的对称点坐标是什么?M(x,y,z)N(x,y,-z)在空间直角坐标系中,点P(1,2,3)关于y轴的对称点是__________________
在空间直角坐标系中,点P(1,2,3)关于x轴的对称点是__________________
在空间直角坐标系中,点P(1,2,3)关于z轴的对称点是__________________(-1,2,-3)(1,-2,-3)(-1,-2,3)巩固练习2在空间直角坐标系中,点P(1,2,3)关于xOy面的对称点是_________________
在空间直角坐标系中,点P(1,2,3)关于yOz面的对称点是_________________
在空间直角坐标系中,点P(1,2,3)关于zOx面的对称点是_________________(1,2,-3)(-1,2,3)(1,-2,3)巩固练习2思考7:在空间直角坐标系Oxyz中,三个坐标平面将空间分成几个部分?每一部分的坐标有何不同?八个卦限中点的坐标符号分别为:
I: ( + ,+ ,+ );
II: ( - ,+ ,+ );
III: ( - ,- ,+ );
IV: ( + ,- ,+ );
V: ( + ,+ ,- );
VI: ( - ,+ ,- );
VII:( - ,- ,- );
VIII:( + ,- ,- );2、在空间直角坐标系中,点 ,过点P作平面yoz的垂线则垂足Q的坐标是?3、点P(-3,1,-2)沿x轴负方向平移2个单位,沿y轴正方向平移1个单位,向z轴正方向平移2个单位得到点P',则点P'的坐标是多少?P(-5,2,0)思考8:设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?思考9:设点A(x1,y1,z1),
点B(x2,y2,z2),则AB的距离如何?空间任意两点间的距离.|P1Q1|=|x1-x2|;|Q1R1|=|y1-y2|;|R1P2|=|z1-z2||P1P2|2=|P1Q1||2+|Q1R1|2+|R1P2|2 已知A(1,-2,11),B(4,2,3),C(6,-1,4),求证其连线组成的三角形为直角三角形。利用两点间距离公式,由从而,根据勾股定理,结论得证。例4 在四面体P-ABCA中,PA、PB、PC两两垂直,设PA=PB=PC=a,求点P到平面ABC的距离。例5ABC 根据题意,建立如图所示的坐标系,则P(0,0,0),A(a,0,0),B(0,a,0),C(0,0,a) 过点P作PH⊥平面ABC,交平面ABC于H,则PH的长即为点P到平面ABC的距离。∵PA=PB=PC,∴H为 的外心,又∵ 为正三角形,∴点P到平面ABC的距离是∴H为 的重心,可得点H的坐标为1.在空间直角坐标系中,已知点P(x,y,z),给出下列4条叙述:
①点P关于x轴的对称点的坐标是(x,-y,z)
②点P关于yOz平面的对称点的坐标是(x,-y,-z)
③点P关于y轴的对称点的坐标是(x,-y,z)
④点P关于原点的对称点的坐标是(-x,-y,-z)
其中正确的个数是(????)
A.3 B.2 C.1 D.0C2.点B是点A(1,2,3)在坐标平面yOz内的射影,则OB等于(????)BA. B. C. D.3.如图,长方体ABCD-A’B’C’D’中,|AD|=3,|AB|=5,|AA’|=3,设E为DB’的中点,F为BC‘的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,A’,B’,C’,D’,E,F各点的坐标。小结1、空间直角坐标系的建立。 2、空间中的点。3、对称点 。4、特殊位置的点的坐标谢谢!
