山东省平原县育才中学2018-2019学年七年级下册数学5.3《平行线的性质》同步测试(含答案)
文档属性
| 名称 | 山东省平原县育才中学2018-2019学年七年级下册数学5.3《平行线的性质》同步测试(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-20 00:00:00 | ||
图片预览



文档简介
2018-2019年七年级数学5.3《平行线的性质》同步测试
一、选择题:
1、下列命题:①若|a|>|b|,那么a2>b2;②两点之间,线段最短;③对顶角相等;④内错角相等.其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
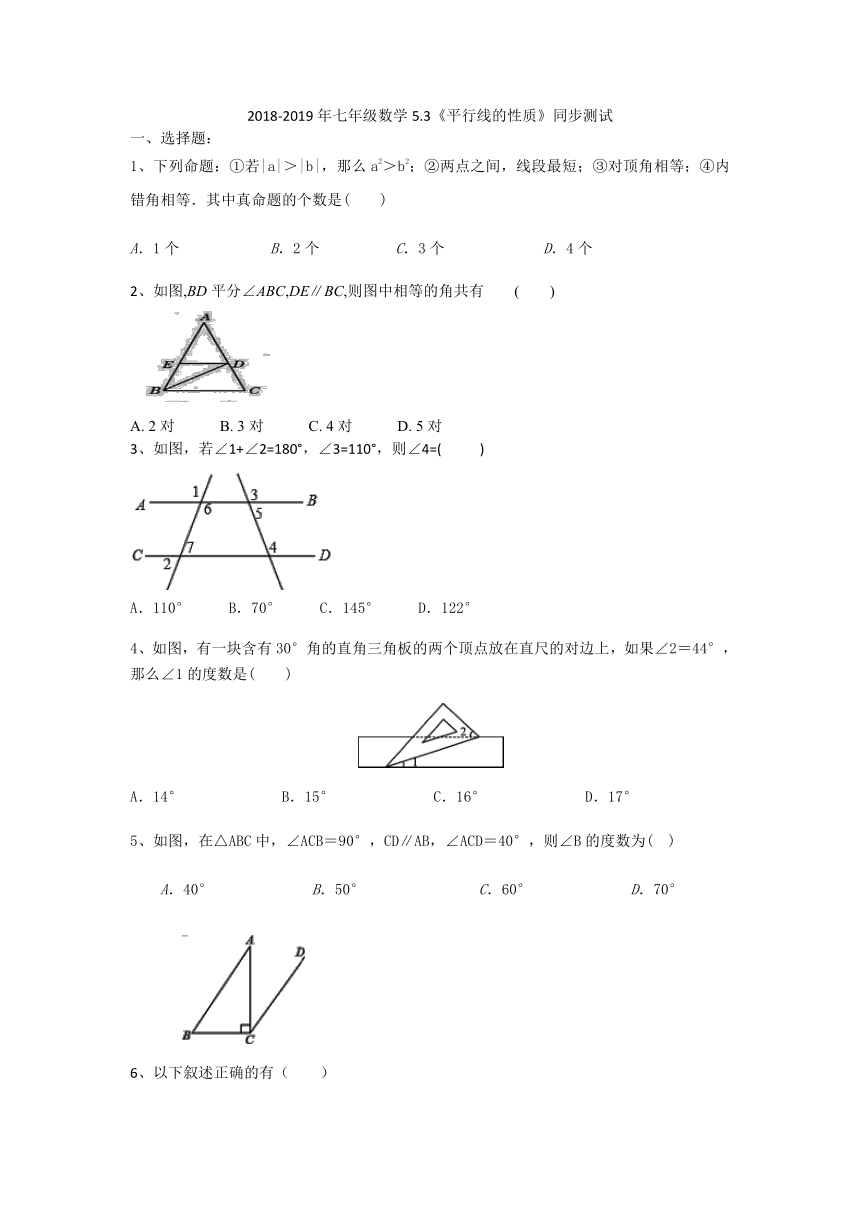
2、如图,BD平分∠ABC,DE∥BC,则图中相等的角共有 ( )
?
A. 2对?????????????B. 3对?????????????C. 4对?????????????D. 5对?????
3、如图,若∠1+∠2=180°,∠3=110°,则∠4=( )
A.110° B.70° C.145° D.122°
4、如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠2=44°,那么∠1的度数是( )
A.14° B.15° C.16° D.17°
5、如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )
A.40° B.50° C.60° D.70°
6、以下叙述正确的有( )
①在同一平面内,不相交的两条直线互相平行;②有公共顶点且有一条公共边的两个角互为邻补角;③如果两条直线被第三条直线所截,那么同位角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直。
A.1个 B.2个 C.3个 D.4个
7、如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东( )
A.42° B.44° C.36° D.22°
8、下列命题正确的是( )
A.同位角相等 B.在同一平面内,若a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角 D.在同一平面内,若a∥b,b∥c,则a∥c
9、如图,a∥b,若要△ABC的面积与△DEF的面积相等,须增加条件 ( )
?
A. AB=DE?????????????B. AC=DF?????????????C. BC=EF?????????????D. BE=AD???????
10、若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A.70° B.70°或86° C.86° D.30°或38°
11、如图,直线a,b被c,d所截,且a∥b,则下列结论中正确的是( )
A.∠1=∠2 C.∠3+∠4=180°
B.∠3=∠4 D.∠1+∠4=180°
12、如图,在Rt△ABC中,∠C=90°,D为边CA延长线上一点,DE∥AB,∠ADE=42°,则∠B的大小为( )
?
A. 42°?????????????B. 45°?????????????C. 48°?????????????D. 58°????????
二、填空题:
13、两个角的两边分别平行,若其中一个角比另一个角的2倍少,则这两个角的度数分别为______ .
14、如图,已知AB∥CD,E在AB与CD之间,且∠B=40°, ∠D=20°.∠BED= .
15、如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD= .
16、如图,已知AB∥DE,∠B=∠E,则BC与EF的位置关系是 .
17、如图,将直角三角板和一把直尺如图放置,若,则的度数是__________.
18、如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数为 .
19、如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF= .
20、如图,小明把一块含有锐角的直角三角板的三个顶点分别放在一组平行线上,如果,那么的度数是______.
21、如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数为 .
22、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,∠2的度数为 .
三、解答题:
23、如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
24、已知如图,AB//CD,∠1=∠3,求证:AC//BD
25、如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是多大?
26、如图,于,交于点,交于点,,,试判断和的位置关系,并说明理由.
27、如图,已知在△ABC中,EF⊥AB,CD⊥AB,G在AC边上,∠AGD=∠ACB.求证:∠1=∠2.
一、选择题:
1、C
2、D
3、A
4、C
5、B
6、B
7、A
8、D
9、C
10、B
11、B
12、C
二、填空题:
13、30°????
14、60°?
15、130°
16、平行
17、47°
18、46°
19、60°????
20、40°
21、55°
22、50
三、解答题:
23、∠C=50°
24、略
25、150°
26、平行
27、∵AB∥CD(已知),
?∴∠AMN=∠DNM(两直线平行,内错角相等).
?∵MQ平分∠AMN,NH平分∠END(已知),
?∴∠QMN=∠AMN,∠HNM=∠MND(角平分线平分的两个角相等).
?∴∠QMN=∠HNM(等量代换).
?∴MQ∥NH(内错角相等,两直线平行).
一、选择题:
1、下列命题:①若|a|>|b|,那么a2>b2;②两点之间,线段最短;③对顶角相等;④内错角相等.其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
2、如图,BD平分∠ABC,DE∥BC,则图中相等的角共有 ( )
?
A. 2对?????????????B. 3对?????????????C. 4对?????????????D. 5对?????
3、如图,若∠1+∠2=180°,∠3=110°,则∠4=( )
A.110° B.70° C.145° D.122°
4、如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠2=44°,那么∠1的度数是( )
A.14° B.15° C.16° D.17°
5、如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )
A.40° B.50° C.60° D.70°
6、以下叙述正确的有( )
①在同一平面内,不相交的两条直线互相平行;②有公共顶点且有一条公共边的两个角互为邻补角;③如果两条直线被第三条直线所截,那么同位角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直。
A.1个 B.2个 C.3个 D.4个
7、如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东( )
A.42° B.44° C.36° D.22°
8、下列命题正确的是( )
A.同位角相等 B.在同一平面内,若a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角 D.在同一平面内,若a∥b,b∥c,则a∥c
9、如图,a∥b,若要△ABC的面积与△DEF的面积相等,须增加条件 ( )
?
A. AB=DE?????????????B. AC=DF?????????????C. BC=EF?????????????D. BE=AD???????
10、若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A.70° B.70°或86° C.86° D.30°或38°
11、如图,直线a,b被c,d所截,且a∥b,则下列结论中正确的是( )
A.∠1=∠2 C.∠3+∠4=180°
B.∠3=∠4 D.∠1+∠4=180°
12、如图,在Rt△ABC中,∠C=90°,D为边CA延长线上一点,DE∥AB,∠ADE=42°,则∠B的大小为( )
?
A. 42°?????????????B. 45°?????????????C. 48°?????????????D. 58°????????
二、填空题:
13、两个角的两边分别平行,若其中一个角比另一个角的2倍少,则这两个角的度数分别为______ .
14、如图,已知AB∥CD,E在AB与CD之间,且∠B=40°, ∠D=20°.∠BED= .
15、如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD= .
16、如图,已知AB∥DE,∠B=∠E,则BC与EF的位置关系是 .
17、如图,将直角三角板和一把直尺如图放置,若,则的度数是__________.
18、如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数为 .
19、如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF= .
20、如图,小明把一块含有锐角的直角三角板的三个顶点分别放在一组平行线上,如果,那么的度数是______.
21、如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数为 .
22、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,∠2的度数为 .
三、解答题:
23、如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
24、已知如图,AB//CD,∠1=∠3,求证:AC//BD
25、如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是多大?
26、如图,于,交于点,交于点,,,试判断和的位置关系,并说明理由.
27、如图,已知在△ABC中,EF⊥AB,CD⊥AB,G在AC边上,∠AGD=∠ACB.求证:∠1=∠2.
一、选择题:
1、C
2、D
3、A
4、C
5、B
6、B
7、A
8、D
9、C
10、B
11、B
12、C
二、填空题:
13、30°????
14、60°?
15、130°
16、平行
17、47°
18、46°
19、60°????
20、40°
21、55°
22、50
三、解答题:
23、∠C=50°
24、略
25、150°
26、平行
27、∵AB∥CD(已知),
?∴∠AMN=∠DNM(两直线平行,内错角相等).
?∵MQ平分∠AMN,NH平分∠END(已知),
?∴∠QMN=∠AMN,∠HNM=∠MND(角平分线平分的两个角相等).
?∴∠QMN=∠HNM(等量代换).
?∴MQ∥NH(内错角相等,两直线平行).
