高中数学第二章统计2.2.2用样本的数字特征估计总体的数字特征课件新人教B版必修3(31张PPT)
文档属性
| 名称 | 高中数学第二章统计2.2.2用样本的数字特征估计总体的数字特征课件新人教B版必修3(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 394.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-20 00:00:00 | ||
图片预览










文档简介
课件31张PPT。2.2.2 用样本的数字特征估计总体的数字特征(二) 知识回顾1.如何根据样本频率分布直方图,分别估计总体的众数、中位数和平均数?(1)众数:最高矩形下端中点的横坐标.(2)中位数:直方图面积平分线与横轴交点的横坐标.(3)平均数:每个小矩形的面积与小矩形底边中点的横坐标的乘积之和. 知识探究:标准差 样本的众数、中位数和平均数常用来表示样本数据的“中心值”,其中众数和中位数容易计算,不受少数几个极端值的影响,但只能表达样本数据中的少量信息. 平均数代表了数据更多的信息,但受样本中每个数据的影响,越极端的数据对平均数的影响也越大.当样本数据质量比较差时,使用众数、中位数或平均数描述数据的中心位置,可能与实际情况产生较大的误差,难以反映样本数据的实际状况,因此,我们需要一个统计数字刻画样本数据的离散程度. 数据的离散程度可以用极差、方差或标准差来描述。 为了表示样本数据的单位表示的波动幅度,通常要求出样本方差或者它的算术平方根. 来衡量这组数据的波动大小,并把它叫做这组数据的方差,一组数据方差越大,则这组数据波动越大。 那么我们用它们的平均数,即(2)标准差:我们把数据的方差的算术平方根叫做这组数据的标准差,它也是一个用来衡量一组数据的波动大小的重要的量。计算标准差的算法: S2 算出每个样本数据与样本平均数的差
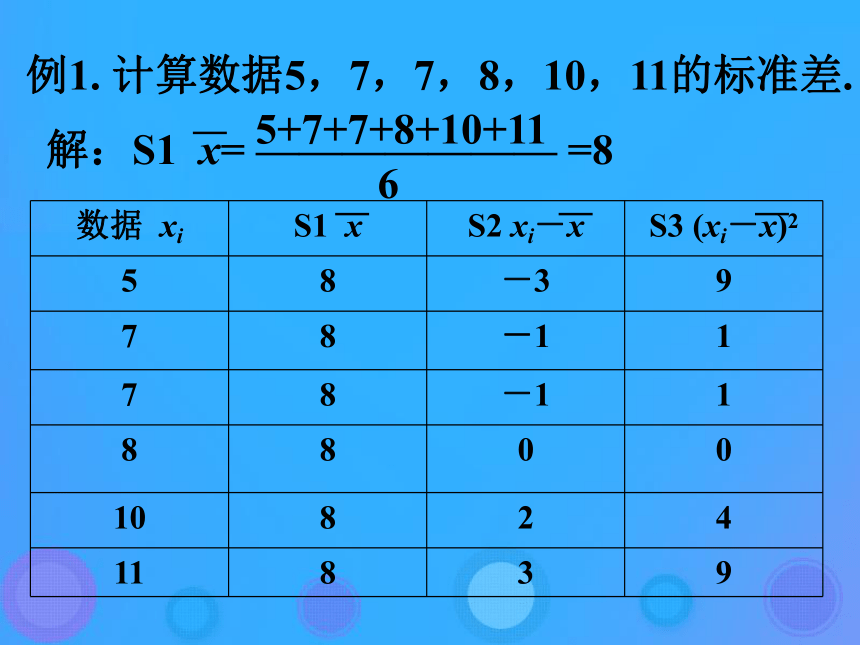
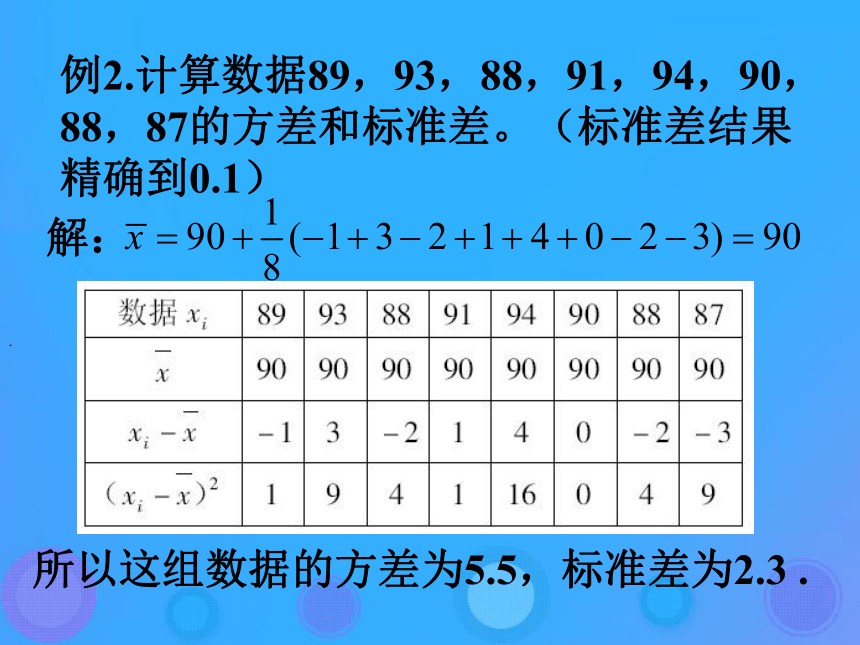
(i=1,2,……,n);S3 算出 (i=1,2,…,n);S4 算出 (i=1,2,…,n)这n个数的平均数,即为样本方差s2;S5 算出方差的算术平方根,即为样本标准差s。(3)方差的运算性质:例1. 计算数据5,7,7,8,10,11的标准差.S5 .所以这组数据的标准差是2.例2.计算数据89,93,88,91,94,90,88,87的方差和标准差。(标准差结果精确到0.1) 解: . 所以这组数据的方差为5.5,标准差为2.3 .例3. 从甲、乙两名学生中选拔一人乘积射击比赛,对他们的射击水平进行测试,两人在相同的条件下各射击10次,命中环数如下﹕
甲﹕7,8,6,8,6,5,8,10,7,4;
乙﹕9,5,7,8,7,6,8,6,7,7.
(1)计算甲、乙两人射击命中环数的平均数和标准差;
(2)比较两人的成绩,然后决定选择哪一人参赛. (2)由(1)知,甲、乙两人平均成绩相等,但s乙 因为0.24>0.02,
所以,由这组数据可以认为甲种水稻的产量比较稳定。 练习2.为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换。已知某校使用的100只日光灯在必须换掉前的使用天数如下,试估计这种日光灯的平均使用寿命和标准差。解:各组中值分别为165,195,225,285,315,345,375,由此算得平均数约为165×1%+195×11%+225×18%+255×20%+285×25%+315×16%+345×7%+375×2%=267.9≈268(天)这些组中值的方差为 [1×(165-268)2+11×(195-268)2+18×(225-268)2+20×(255-268)2+25×(285-268)2+16× (315-268)2+7×(345-268)2+2×(375-268)2] ÷100=2128.60(天2).故所求的标准差约 (天)答:估计这种日光灯的平均使用寿命约为268天,标准差约为46天.3.(2011年高考江苏卷6)某老师从星期一到星
期五收到信件数分别是10,6,8,5,6,则
该组数据的方差( )
3.24.(2011年高考辽宁卷文科19) (本小题满分12分)
某农场计划种植某种新作物.为此对这种作物的两个品种
(分别称为品种甲和品种乙)进行田间试验,选取两大块地,
每大块地分成n小块地,在总共2n小块地中.随机选n小块
地种植品种甲,另外n小块地种植品种乙
(Ⅰ)假设n=2,求第一大块地都种植品种甲的概率:
(Ⅱ)试验时每大块地分成8小块.即n=8,试验结束后得到
品种甲和品种乙在各小块地上的每公顷产量(单位kg/hm2)
如下:
分别求品种甲和品种乙的每公顷产量的样本平均数和样本
方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据x1,x2…xa的样本方差,
其中 为样本平均数。由以上结果可以看出,品种乙的样本平均
数大于品种甲的样本平均数,
且两品种的样本方差差异不大,故应该选
择种植品种乙。5.(2011年高考北京卷理科17)本小题共13分
以下茎叶图记录了甲、乙两组个四名同学的植树棵树。
乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率. 解:(1)当X=8时,由茎叶图可知,乙组同学的植树棵数
是:8,8,9,10,所以平均数为
方差为
6.(2011年高考广东卷文科17)(本小题满分13分)
在某次测验中,有6位同学的平均成绩为75分.用表示编
号为的同学所得成绩,且前5位同学的成绩如下:
(1)求第6位同学成绩,及这6位同学成绩的标准差;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间中的概率.6.练习:(3)若k1,k2,…, k8的方差为3,则2(k1-3),
2(k2-3), …, 2(k8-3)的方差为________43212AB7。在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为________9.5,0.0161.用样本的数字特征估计总体的数字特征分两类:
用样本平均数估计总体平均数。
用样本方差、标准差估计总体方差、标准差。样本容量越大,估计就越精确。
2.方差、标准差描述一组数据围绕平均数波动的大小,反映了一组数据变化的幅度.回顾小结
(i=1,2,……,n);S3 算出 (i=1,2,…,n);S4 算出 (i=1,2,…,n)这n个数的平均数,即为样本方差s2;S5 算出方差的算术平方根,即为样本标准差s。(3)方差的运算性质:例1. 计算数据5,7,7,8,10,11的标准差.S5 .所以这组数据的标准差是2.例2.计算数据89,93,88,91,94,90,88,87的方差和标准差。(标准差结果精确到0.1) 解: . 所以这组数据的方差为5.5,标准差为2.3 .例3. 从甲、乙两名学生中选拔一人乘积射击比赛,对他们的射击水平进行测试,两人在相同的条件下各射击10次,命中环数如下﹕
甲﹕7,8,6,8,6,5,8,10,7,4;
乙﹕9,5,7,8,7,6,8,6,7,7.
(1)计算甲、乙两人射击命中环数的平均数和标准差;
(2)比较两人的成绩,然后决定选择哪一人参赛. (2)由(1)知,甲、乙两人平均成绩相等,但s乙
所以,由这组数据可以认为甲种水稻的产量比较稳定。 练习2.为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换。已知某校使用的100只日光灯在必须换掉前的使用天数如下,试估计这种日光灯的平均使用寿命和标准差。解:各组中值分别为165,195,225,285,315,345,375,由此算得平均数约为165×1%+195×11%+225×18%+255×20%+285×25%+315×16%+345×7%+375×2%=267.9≈268(天)这些组中值的方差为 [1×(165-268)2+11×(195-268)2+18×(225-268)2+20×(255-268)2+25×(285-268)2+16× (315-268)2+7×(345-268)2+2×(375-268)2] ÷100=2128.60(天2).故所求的标准差约 (天)答:估计这种日光灯的平均使用寿命约为268天,标准差约为46天.3.(2011年高考江苏卷6)某老师从星期一到星
期五收到信件数分别是10,6,8,5,6,则
该组数据的方差( )
3.24.(2011年高考辽宁卷文科19) (本小题满分12分)
某农场计划种植某种新作物.为此对这种作物的两个品种
(分别称为品种甲和品种乙)进行田间试验,选取两大块地,
每大块地分成n小块地,在总共2n小块地中.随机选n小块
地种植品种甲,另外n小块地种植品种乙
(Ⅰ)假设n=2,求第一大块地都种植品种甲的概率:
(Ⅱ)试验时每大块地分成8小块.即n=8,试验结束后得到
品种甲和品种乙在各小块地上的每公顷产量(单位kg/hm2)
如下:
分别求品种甲和品种乙的每公顷产量的样本平均数和样本
方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据x1,x2…xa的样本方差,
其中 为样本平均数。由以上结果可以看出,品种乙的样本平均
数大于品种甲的样本平均数,
且两品种的样本方差差异不大,故应该选
择种植品种乙。5.(2011年高考北京卷理科17)本小题共13分
以下茎叶图记录了甲、乙两组个四名同学的植树棵树。
乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率. 解:(1)当X=8时,由茎叶图可知,乙组同学的植树棵数
是:8,8,9,10,所以平均数为
方差为
6.(2011年高考广东卷文科17)(本小题满分13分)
在某次测验中,有6位同学的平均成绩为75分.用表示编
号为的同学所得成绩,且前5位同学的成绩如下:
(1)求第6位同学成绩,及这6位同学成绩的标准差;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间中的概率.6.练习:(3)若k1,k2,…, k8的方差为3,则2(k1-3),
2(k2-3), …, 2(k8-3)的方差为________43212AB7。在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为________9.5,0.0161.用样本的数字特征估计总体的数字特征分两类:
用样本平均数估计总体平均数。
用样本方差、标准差估计总体方差、标准差。样本容量越大,估计就越精确。
2.方差、标准差描述一组数据围绕平均数波动的大小,反映了一组数据变化的幅度.回顾小结
