高中数学人教B版必修1第三章基本初等函数(Ⅰ)3.2.3指数函数和对数函数的关系课件(26张PPT)
文档属性
| 名称 | 高中数学人教B版必修1第三章基本初等函数(Ⅰ)3.2.3指数函数和对数函数的关系课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 484.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-20 00:00:00 | ||
图片预览





文档简介
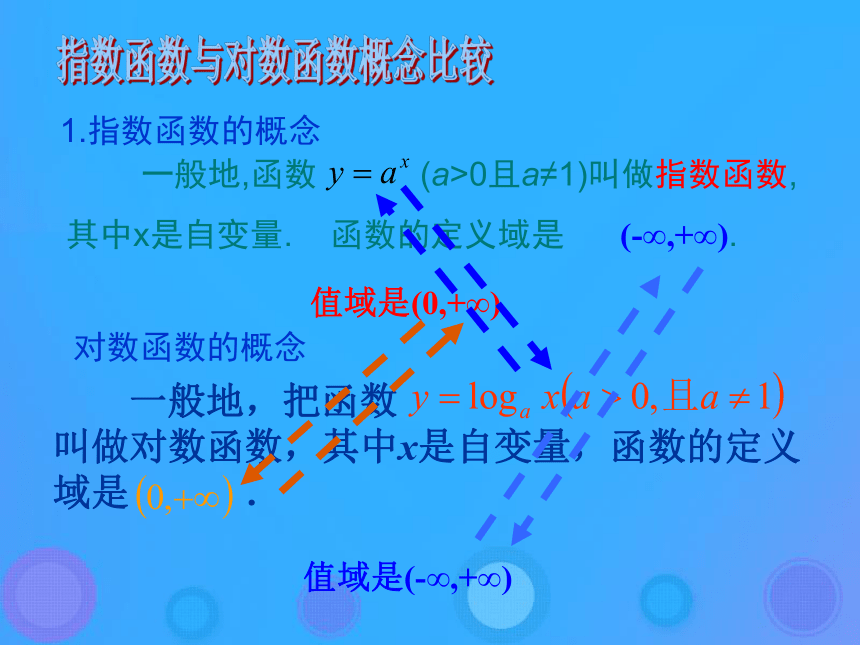
课件26张PPT。指数函数与对数函数的关系指数函数与对数函数概念比较 一般地,把函数 叫做对数函数,其中x是自变量,函数的定义域是 . 一般地,函数 (a>0且a≠1)叫做指数函数,
其中x是自变量. 函数的定义域是 (-∞,+∞). 1.指数函数的概念对数函数的概念值域是(-∞,+∞)值域是(0,+∞) 一般地,把函数 叫做对数函数,其中x是自变量,函数的定义域是 . 一般地,函数 (a>0且a≠1)叫做指数函数,
其中x是自变量. 函数的定义域是 (-∞,+∞). 1.指数函数的概念对数函数的概念值域是(-∞,+∞)值域是(0,+∞)指数函数与对数函数概念比较 对比同以a(a>0且a≠1)为底数的对数函数和
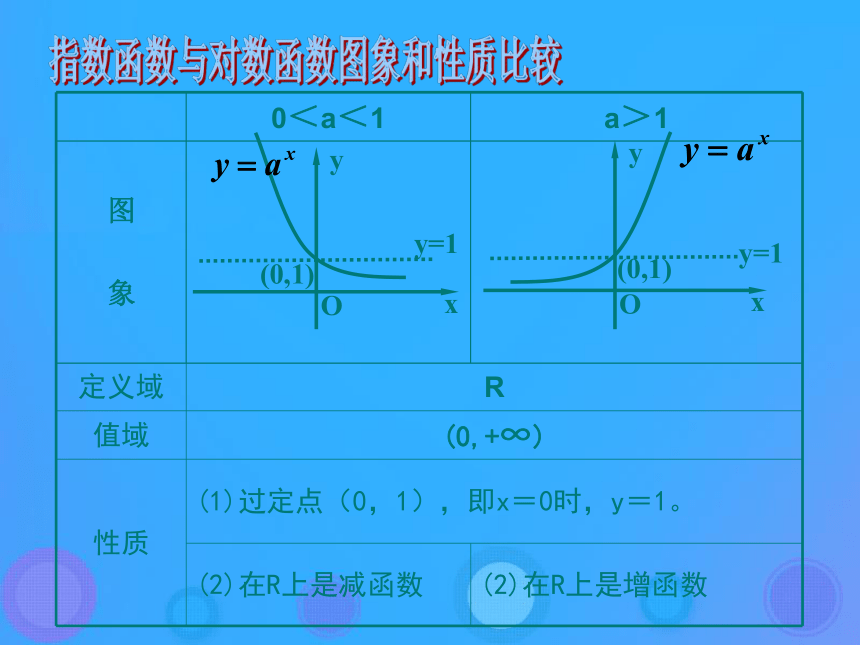
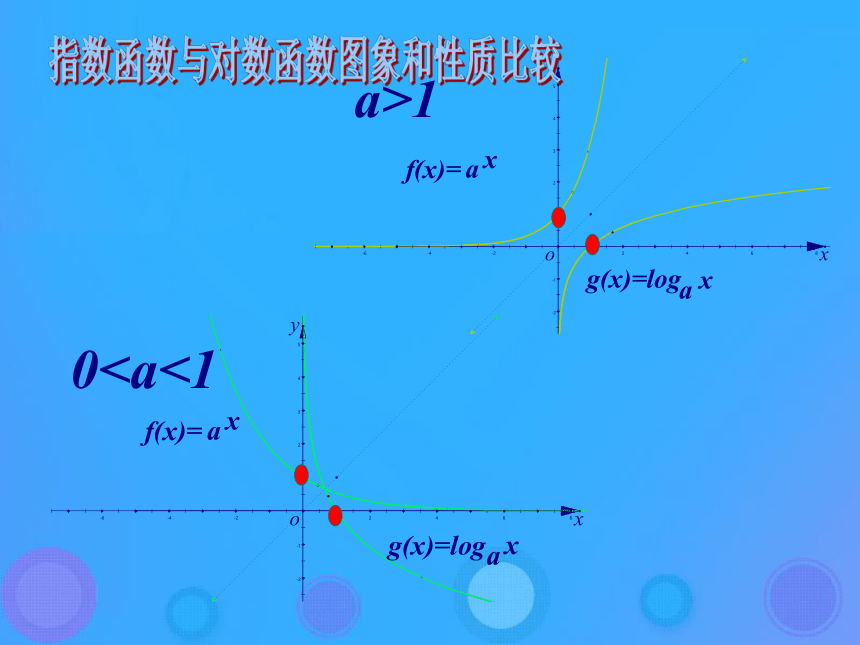
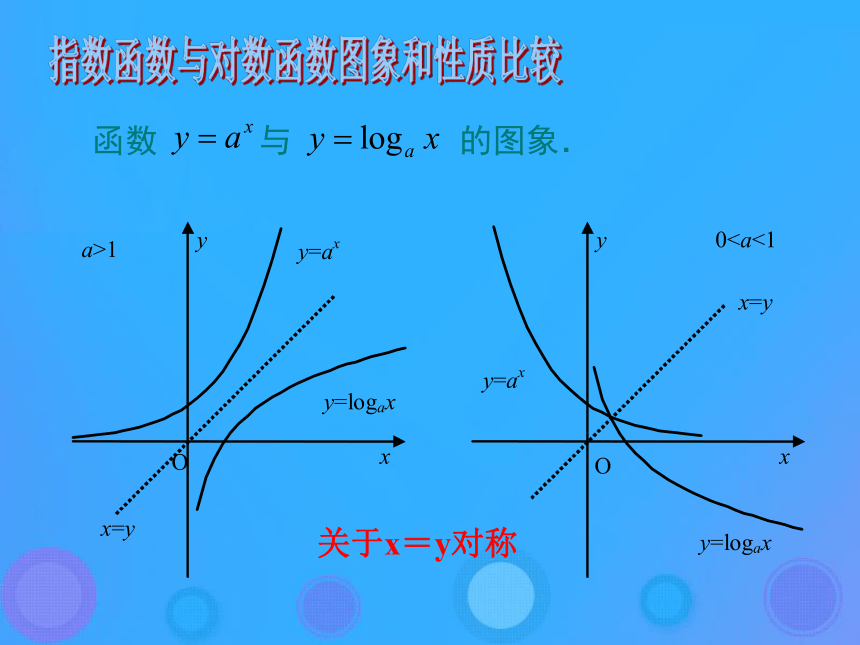
指数函数,看看自变量与函数值之间有什么关系?两函数的定义域和值域交叉对应。指数函数与对数函数概念比较指数函数与对数函数图象和性质比较a>10指数函数,看看两函数的图像之间有什么关系?两函数的图像总是关于直线y=x对称。指数函数与对数函数图象和性质比较 同以a(a>0且a≠1)为底数的对数函数和指数函数,看看自变量与函数值之间、两函数的图像之间有什么关系:⑴两函数的定义域和值域交叉对应;⑵两函数的图像总是关于直线y=x对称。图象和性质比较结果及反函数的意义 像这样以a为底的对数函数,自变量x和函数值y分别是以a为底的指数函数的函数值和自变量,我们称有这种特殊关系的两个函数互为反函数. 1.反函数定义 一般地,函数y=f(x) (x ∈A),设它的值域为C,我们根据这个函数中x,y的关系,用y把x表示出,得到x= φ(y) ,如果对于 y在 C中的任何一个值,通过x= φ(y) ,x在A中都有唯一的值和它对应,那么,x= φ(y) 就表示y是自变量,x是自变量y的函数,这样的函数x= φ(y) (y ∈C)叫做函数y=f(x)(x∈A)的反函数.记作:x=f-1(y). 反函数x=f-1(y)中,x为因变量,y为自变量,为和习惯一致,将x,y互换得: y=f-1(x) ( x∈C).知识要点思考:
是否所有的函数都有反函数?f(x)=x2有没有反函数?
f(x)=x2, 有没有反函数?结论:
只有函数对应的映射是一一映射时,才有反函数。小试牛刀2.求反函数的方法步骤:③求出原函数的值域;即求出反函数的定义域;①由 y = f ( x ) 反解出 x = f -1 ( y )(把 x 用 y 表 示出来);②将 x = f -1 ( y ) 改写成 y = f -1 ( x ),并写出反函数的 定义域(对调 x = f -1 ( y ) 中的 x、y).如何求一个函数的反函数呢?提示:一定要注意原函数的值域。在求解反函数时,往往都要写出相应的定义域。范例例1 求下列函数的反函数:解:⑴例1 求下列函数的反函数:解:⑵范例例1 求下列函数的反函数:解:⑶范例例1 求下列函数的反函数:解:⑷范例3.原函数与反函数的联系4.互为反函数的函数图象间的关系 一般地,函数y=f(x)的图像和它的反函数y= f-1(x) 的图像关于直线y=x对称.其增减性相同.释意:如果点(a,b)在函数y=f(x)的图像上,那么点(b,a)必然在它的反函数y=f-1(x)的图像上。换言之,如果函数y=f(x)的图像上有点(a,b),那么它的反函数y=f-1(x)的图像上必然有点(b,a).知识要点例2 函数f(x)=loga (x-1)(a>0且a≠1)
的反函数的图象经过点(1, 4),求a的值. 若函数y=f(x)的图象经过点(a, b),
则其反函数的图象经过点(b, a).小 结:解:依题意,得 思考如下问题:1、互为反函数的两个函数的单调性有怎样的关系?
2、如果一个函数是偶函数,它有没有反函数?奇函数呢?如果有,它的反函数的奇偶性是怎样的?
关于反函数,你认识到了多少呢?请列出??几个重要的结论1、互为反函数的两个函数的单调性一致;
2、若一奇函数有反函数,则它的反函数也是奇函数;若函数为偶函数,则它没有反函数;
3、若点P(m,n)在y=f(x)的图象上,则点P’(n,m)在其反函数的图象上。快乐体验快乐体验课堂小结(1)指数函数、对数函数的概念;(2)指数函数、对数函数的图象与性质;(3)反函数的概念及求解步骤;再见!谢谢大家!点滴积累 丰富人生
其中x是自变量. 函数的定义域是 (-∞,+∞). 1.指数函数的概念对数函数的概念值域是(-∞,+∞)值域是(0,+∞) 一般地,把函数 叫做对数函数,其中x是自变量,函数的定义域是 . 一般地,函数 (a>0且a≠1)叫做指数函数,
其中x是自变量. 函数的定义域是 (-∞,+∞). 1.指数函数的概念对数函数的概念值域是(-∞,+∞)值域是(0,+∞)指数函数与对数函数概念比较 对比同以a(a>0且a≠1)为底数的对数函数和
指数函数,看看自变量与函数值之间有什么关系?两函数的定义域和值域交叉对应。指数函数与对数函数概念比较指数函数与对数函数图象和性质比较a>10
f(x)=x2, 有没有反函数?结论:
只有函数对应的映射是一一映射时,才有反函数。小试牛刀2.求反函数的方法步骤:③求出原函数的值域;即求出反函数的定义域;①由 y = f ( x ) 反解出 x = f -1 ( y )(把 x 用 y 表 示出来);②将 x = f -1 ( y ) 改写成 y = f -1 ( x ),并写出反函数的 定义域(对调 x = f -1 ( y ) 中的 x、y).如何求一个函数的反函数呢?提示:一定要注意原函数的值域。在求解反函数时,往往都要写出相应的定义域。范例例1 求下列函数的反函数:解:⑴例1 求下列函数的反函数:解:⑵范例例1 求下列函数的反函数:解:⑶范例例1 求下列函数的反函数:解:⑷范例3.原函数与反函数的联系4.互为反函数的函数图象间的关系 一般地,函数y=f(x)的图像和它的反函数y= f-1(x) 的图像关于直线y=x对称.其增减性相同.释意:如果点(a,b)在函数y=f(x)的图像上,那么点(b,a)必然在它的反函数y=f-1(x)的图像上。换言之,如果函数y=f(x)的图像上有点(a,b),那么它的反函数y=f-1(x)的图像上必然有点(b,a).知识要点例2 函数f(x)=loga (x-1)(a>0且a≠1)
的反函数的图象经过点(1, 4),求a的值. 若函数y=f(x)的图象经过点(a, b),
则其反函数的图象经过点(b, a).小 结:解:依题意,得 思考如下问题:1、互为反函数的两个函数的单调性有怎样的关系?
2、如果一个函数是偶函数,它有没有反函数?奇函数呢?如果有,它的反函数的奇偶性是怎样的?
关于反函数,你认识到了多少呢?请列出??几个重要的结论1、互为反函数的两个函数的单调性一致;
2、若一奇函数有反函数,则它的反函数也是奇函数;若函数为偶函数,则它没有反函数;
3、若点P(m,n)在y=f(x)的图象上,则点P’(n,m)在其反函数的图象上。快乐体验快乐体验课堂小结(1)指数函数、对数函数的概念;(2)指数函数、对数函数的图象与性质;(3)反函数的概念及求解步骤;再见!谢谢大家!点滴积累 丰富人生
