高中数学 人教B版必修1第二章函数2.1.1函数—变量与函数的概念(第一课时)课件(23张)
文档属性
| 名称 | 高中数学 人教B版必修1第二章函数2.1.1函数—变量与函数的概念(第一课时)课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-20 00:00:00 | ||
图片预览






文档简介
课件23张PPT。第二章 函数
2.1.1 函数(一)
—变量与函数的概念
复习提问1.初中所学的函数的概念是什么?在一个变化过程中,有两个变量x和y,如果给定一个x值,
相应地就确定唯一的一个y值, 那么就称y是x的函数,其
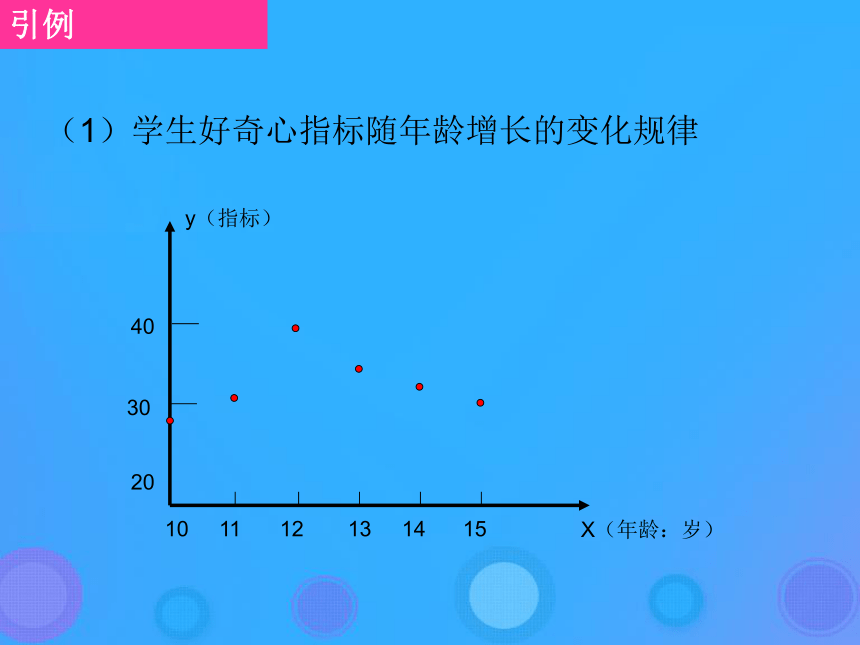
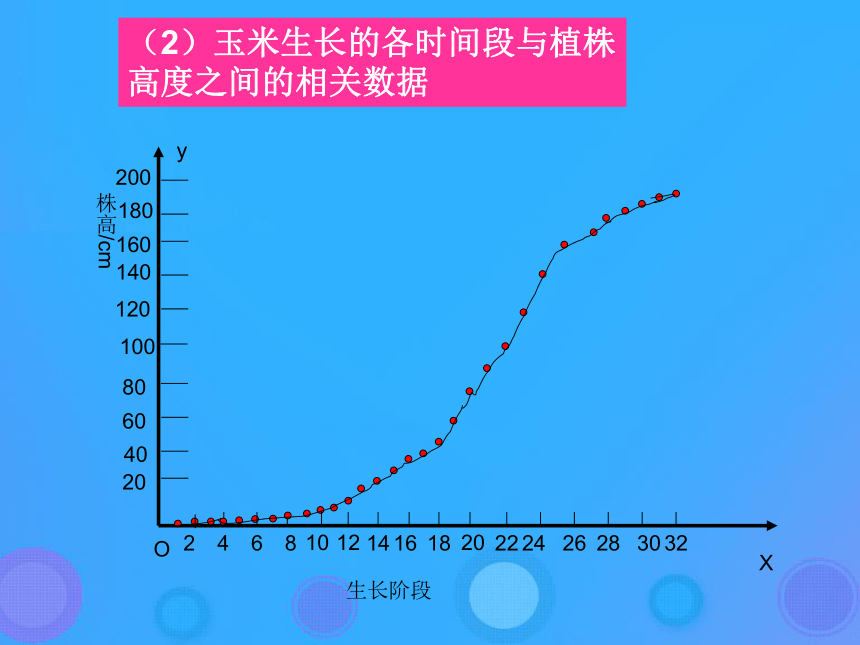
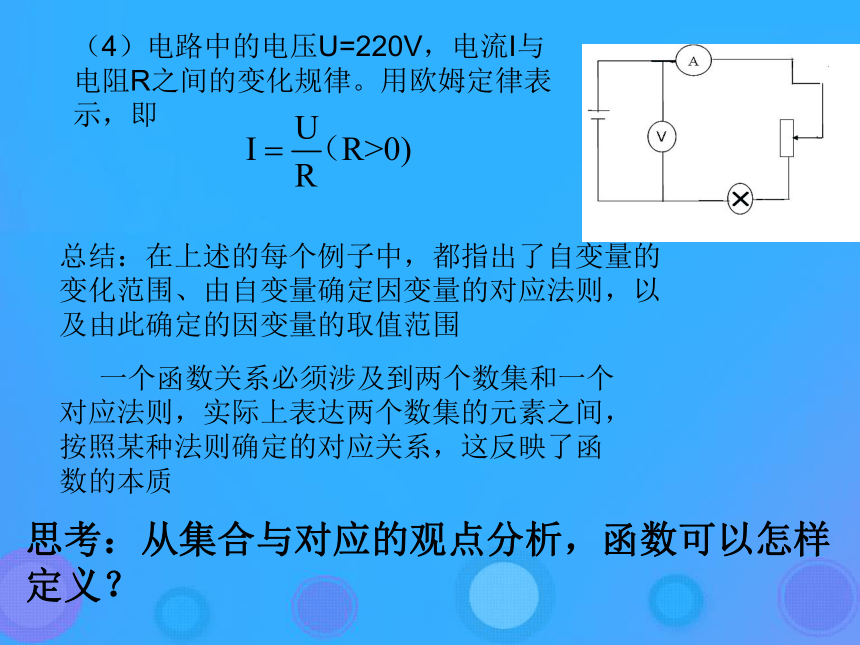
中x是自变量,y是因变量.2.初中学过哪些函数?正比例函数、反比例函数、一次函数、二次函数等.引例(1)学生好奇心指标随年龄增长的变化规律(2)玉米生长的各时间段与植株高度之间的相关数据(4)电路中的电压U=220V,电流I与电阻R之间的变化规律。用欧姆定律表示,即总结:在上述的每个例子中,都指出了自变量的变化范围、由自变量确定因变量的对应法则,以及由此确定的因变量的取值范围 一个函数关系必须涉及到两个数集和一个对应法则,实际上表达两个数集的元素之间,按照某种法则确定的对应关系,这反映了函数的本质思考:从集合与对应的观点分析,函数可以怎样定义? 设集合A是一个非空的数集,对A中的任意数x , 按照确定的法则f,都有唯一确定的数y与它对应, 则这种对应关系叫做集合A上的一个函数.记作:
y=f (x),x?A
其中x叫做自变量,自变量的取值范围(数集A)叫做这个函数的定义域。一、形成概念1. 定义 如果自变量取值 a,则由法则 f 确定的值 y 称为函数在 a 处的函数值,记作:
y=f(a) 或 y|x=a
所有函数值构成的集合 {y|y=f (x),x∈A} 叫做这个函数的值域。
函数y=f (x)也经常写作函数 f 或函数f (x)二、函数的二要素: 定义域A; 对应法则 f.说明:(1)函数符号y=f (x) 表示y是x的函数, f (x)不是表示 f 与x的乘积;(3)“y=f (x)”是函数符号,可以用任意的字母表示,如:“y=g(x)”;(2) f 表示对应法则,不同函数中f 的具体含义不一样;三、区 间a与b叫做区间的端点,在数轴上表示区间时,属于这个区间端点的实数,用实心点表示,不属于这个区间端点的实数,用空心点表示.四、判断两个是否具有函数关系,只要检验:
(1)定义域和对应法则是否给出:
(2)根据给出的对应法则,自变量x在其定义
域中的每一个值,是否都能确定唯一的函数值y
五、同一函数函数与函数之间只要定义域和对应法则都相同,就是同一函数例1 下列各组式子是否表示同一函数?为什么?
,是否否练习:下列各图中,可表示函数y=f(x)的图
象的只可能是( )
D判断下列图象能表示函数图象的是( )D例2. 试用区间表示下列实数集
(1){x|5 ≤ x<6}
(2) {x|x ≥9}
(3) {x|x ≤ -1} ∩{x| -5 ≤ x<2}
(4) {x|x < -9}∪{x| 9 < x<20}例3. .求下列函数的定义域: 思考:给出解析式的函数的定义域
需注意什么? 当函数是由解析式给出时,其定义域就是使函数解析式有意义的自变量的取值集合
(1)如果f(x)是整式,那么函数的定义域是实数集R;
(2)如果f(x)是分式,那么函数的定义域是使分母不为0
的实数的集合;
(3)如果f(x)为二次根式,那么函数的定义域是使根号的
式子大于或等于0的实数的集合;
(4)如果f(x)是由几个部分的数学式子构成的,那么函数
的定义域是使各部分式子都有意义的实数的集合解:2.求下列函数的定义域快乐体验 (3) (4)
1.函数的定义
2.定义域求法
3.如何检验两个变量之间是否具有函数关系
4.区间的相关概念课堂小结
2.1.1 函数(一)
—变量与函数的概念
复习提问1.初中所学的函数的概念是什么?在一个变化过程中,有两个变量x和y,如果给定一个x值,
相应地就确定唯一的一个y值, 那么就称y是x的函数,其
中x是自变量,y是因变量.2.初中学过哪些函数?正比例函数、反比例函数、一次函数、二次函数等.引例(1)学生好奇心指标随年龄增长的变化规律(2)玉米生长的各时间段与植株高度之间的相关数据(4)电路中的电压U=220V,电流I与电阻R之间的变化规律。用欧姆定律表示,即总结:在上述的每个例子中,都指出了自变量的变化范围、由自变量确定因变量的对应法则,以及由此确定的因变量的取值范围 一个函数关系必须涉及到两个数集和一个对应法则,实际上表达两个数集的元素之间,按照某种法则确定的对应关系,这反映了函数的本质思考:从集合与对应的观点分析,函数可以怎样定义? 设集合A是一个非空的数集,对A中的任意数x , 按照确定的法则f,都有唯一确定的数y与它对应, 则这种对应关系叫做集合A上的一个函数.记作:
y=f (x),x?A
其中x叫做自变量,自变量的取值范围(数集A)叫做这个函数的定义域。一、形成概念1. 定义 如果自变量取值 a,则由法则 f 确定的值 y 称为函数在 a 处的函数值,记作:
y=f(a) 或 y|x=a
所有函数值构成的集合 {y|y=f (x),x∈A} 叫做这个函数的值域。
函数y=f (x)也经常写作函数 f 或函数f (x)二、函数的二要素: 定义域A; 对应法则 f.说明:(1)函数符号y=f (x) 表示y是x的函数, f (x)不是表示 f 与x的乘积;(3)“y=f (x)”是函数符号,可以用任意的字母表示,如:“y=g(x)”;(2) f 表示对应法则,不同函数中f 的具体含义不一样;三、区 间a与b叫做区间的端点,在数轴上表示区间时,属于这个区间端点的实数,用实心点表示,不属于这个区间端点的实数,用空心点表示.四、判断两个是否具有函数关系,只要检验:
(1)定义域和对应法则是否给出:
(2)根据给出的对应法则,自变量x在其定义
域中的每一个值,是否都能确定唯一的函数值y
五、同一函数函数与函数之间只要定义域和对应法则都相同,就是同一函数例1 下列各组式子是否表示同一函数?为什么?
,是否否练习:下列各图中,可表示函数y=f(x)的图
象的只可能是( )
D判断下列图象能表示函数图象的是( )D例2. 试用区间表示下列实数集
(1){x|5 ≤ x<6}
(2) {x|x ≥9}
(3) {x|x ≤ -1} ∩{x| -5 ≤ x<2}
(4) {x|x < -9}∪{x| 9 < x<20}例3. .求下列函数的定义域: 思考:给出解析式的函数的定义域
需注意什么? 当函数是由解析式给出时,其定义域就是使函数解析式有意义的自变量的取值集合
(1)如果f(x)是整式,那么函数的定义域是实数集R;
(2)如果f(x)是分式,那么函数的定义域是使分母不为0
的实数的集合;
(3)如果f(x)为二次根式,那么函数的定义域是使根号的
式子大于或等于0的实数的集合;
(4)如果f(x)是由几个部分的数学式子构成的,那么函数
的定义域是使各部分式子都有意义的实数的集合解:2.求下列函数的定义域快乐体验 (3) (4)
1.函数的定义
2.定义域求法
3.如何检验两个变量之间是否具有函数关系
4.区间的相关概念课堂小结
