高中数学 人教B版必修4第一章基本初等函数(II)1.3.2正弦函数的图象与性质课件(20张)
文档属性
| 名称 | 高中数学 人教B版必修4第一章基本初等函数(II)1.3.2正弦函数的图象与性质课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-20 22:20:56 | ||
图片预览






文档简介
课件20张PPT。正弦函数的图象和性质三角函数是高考的重点,也是高考的热点.一般
设计一道或两道客观题,一道解答题,约占总分的
13%,即20分左右.多数是中、低档题.近几年高考
已逐步抛弃了对复杂三角变换和特殊技巧的考查,而重点转移到对三角函数的图象与性质、对基础知识和基本技能的考查上来.
在考查三角公式进行恒等变形的同时,直接考
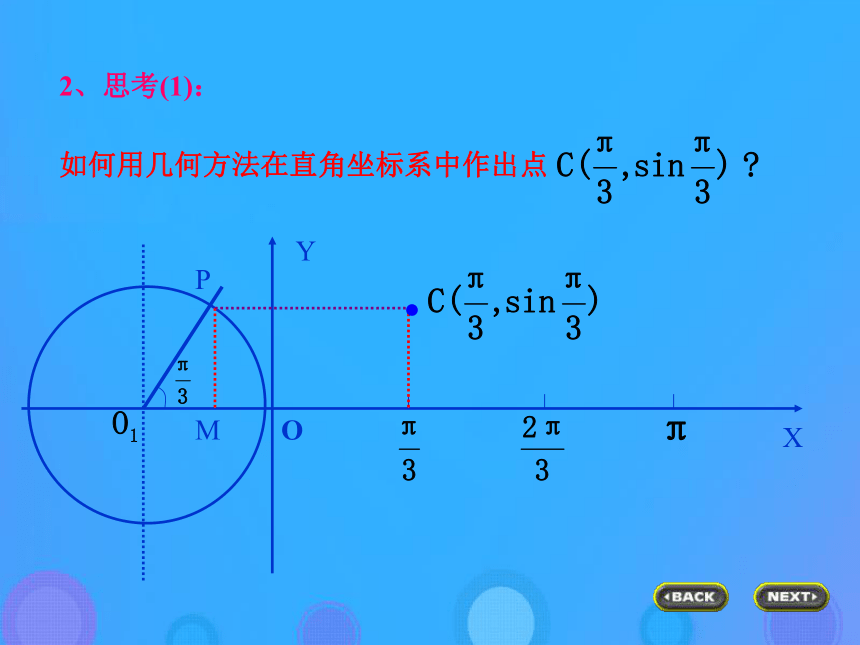
查三角函数的性质及图象的变换,即加强了对三角函数性质和图象的考查力度.(1) 列表(2) 描点(3) 连线1.用描点法作出函数图象的主要步骤是什么?2、思考(1):如何用几何方法在直角坐标系中作出点OPMXY.思考(2): 能否借助上面作点C的方法,
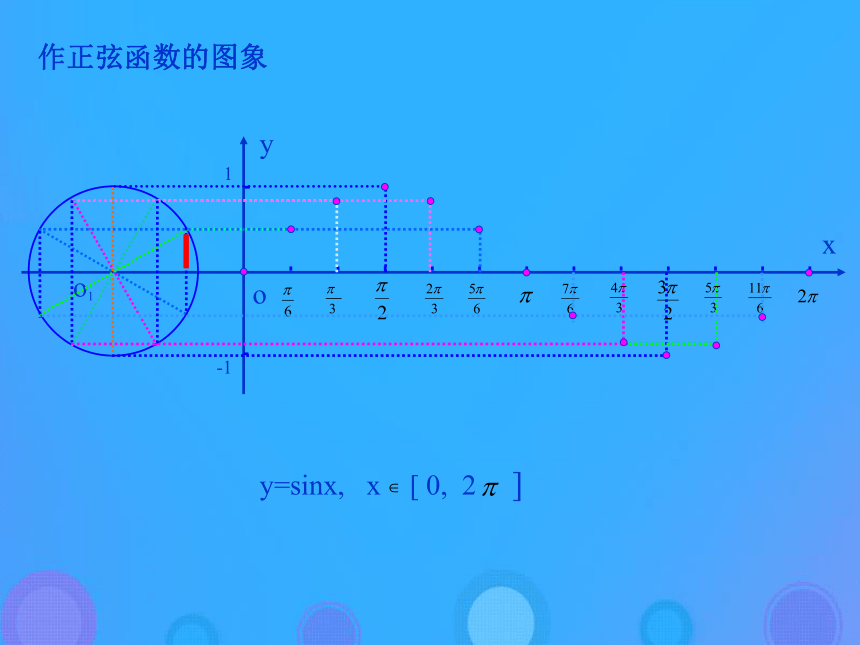
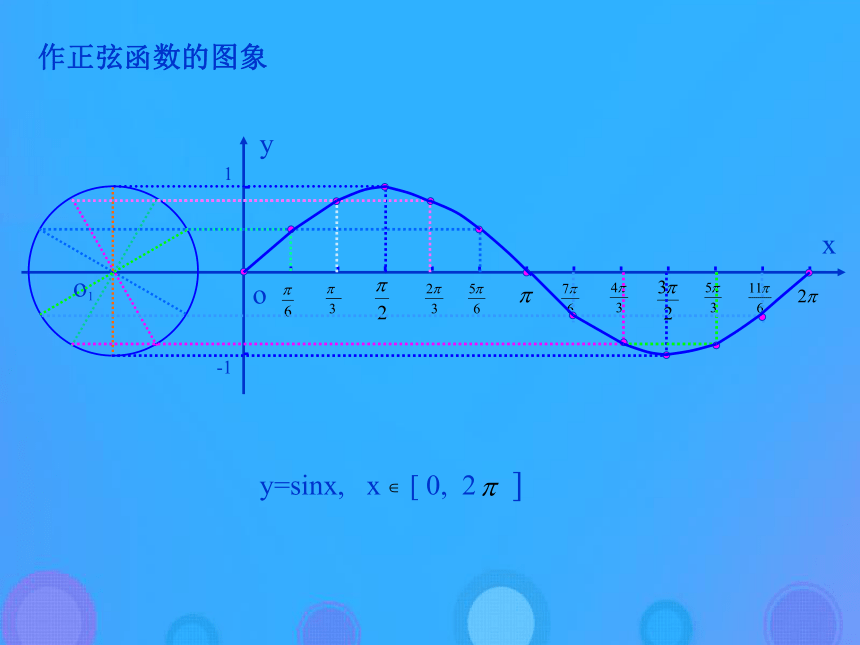
在直角坐标系中作出正弦函数 的图象呢?作正弦函数的图象o1xyy=sinx, x [ 0, 2 ]o-11y=sinx x?[0,2?]y=sinx x?R终边相同角的三角函数值相等 即: sin(x+2k?)=sinx, k?Z 利用图象平移正弦曲线与x轴的交点图象的最高点图象的最低点(五点作图法)列表(2)描点作图(1)y=2sinx , x∈[0,2π]例1.分别作出下列函数简图(五点法作图)0 ? 2?0 2 0 -2 0Y2X0y=2sinx y=2sinx1y=sinx列表(2)描点作图(2)y=sin2x , x∈[0,π]2、五点作图法0 ? 2?2x0 1 0 -1 00 ?Y1X0y=sin2x y=sin2x正弦函数y=sinx的性质:(4)最大值与最小值正弦函数y=sinx的性质:例2 求y= 5+sinx这个函数的最大值、最小值和 周期,并求这个函数分别取得最大值及最小值的x的集合。使y= 5+sinx取得最大值的x的集合是:使y= 5+sinx取得最小值的x的集合是:解:变式:设sinx=t-3,x∈R,求t的取值范围。例3.不通过求,指出下列各式大于零还是
小于零C快乐体验小结:1、用单位圆中的正弦线画出正弦函数的图象。2、利用五点法作正弦函数的简图。3 、观察图象得出正弦函数的性质三角函数是中学数学的主体内容,是高考的重点,
也是高考的热点,其考点主要包括:同角三角关系
式及诱导公式,三角函数的图象和性质,三角函数
的化简求值,三角形中的三角函数,三角函数的最
值及综合应用。一般设计一道或两道客观题,一
道解答题,约占总分的13%,即20分左右.多数是中、
低档题.近几年高考已逐步抛弃了对复杂三角变换
和特殊技巧的考查,而重点转移到对三角函数的
图象与性质的考查,对基础知识和基本技能的考查
上来.在考查三角公式进行恒等变形的同时,也直
接考查了三角函数的性质及图象的变换,降低了
对三角函数恒等变形的要求,加强了对三角函数
性质和图象的考查力度.
设计一道或两道客观题,一道解答题,约占总分的
13%,即20分左右.多数是中、低档题.近几年高考
已逐步抛弃了对复杂三角变换和特殊技巧的考查,而重点转移到对三角函数的图象与性质、对基础知识和基本技能的考查上来.
在考查三角公式进行恒等变形的同时,直接考
查三角函数的性质及图象的变换,即加强了对三角函数性质和图象的考查力度.(1) 列表(2) 描点(3) 连线1.用描点法作出函数图象的主要步骤是什么?2、思考(1):如何用几何方法在直角坐标系中作出点OPMXY.思考(2): 能否借助上面作点C的方法,
在直角坐标系中作出正弦函数 的图象呢?作正弦函数的图象o1xyy=sinx, x [ 0, 2 ]o-11y=sinx x?[0,2?]y=sinx x?R终边相同角的三角函数值相等 即: sin(x+2k?)=sinx, k?Z 利用图象平移正弦曲线与x轴的交点图象的最高点图象的最低点(五点作图法)列表(2)描点作图(1)y=2sinx , x∈[0,2π]例1.分别作出下列函数简图(五点法作图)0 ? 2?0 2 0 -2 0Y2X0y=2sinx y=2sinx1y=sinx列表(2)描点作图(2)y=sin2x , x∈[0,π]2、五点作图法0 ? 2?2x0 1 0 -1 00 ?Y1X0y=sin2x y=sin2x正弦函数y=sinx的性质:(4)最大值与最小值正弦函数y=sinx的性质:例2 求y= 5+sinx这个函数的最大值、最小值和 周期,并求这个函数分别取得最大值及最小值的x的集合。使y= 5+sinx取得最大值的x的集合是:使y= 5+sinx取得最小值的x的集合是:解:变式:设sinx=t-3,x∈R,求t的取值范围。例3.不通过求,指出下列各式大于零还是
小于零C快乐体验小结:1、用单位圆中的正弦线画出正弦函数的图象。2、利用五点法作正弦函数的简图。3 、观察图象得出正弦函数的性质三角函数是中学数学的主体内容,是高考的重点,
也是高考的热点,其考点主要包括:同角三角关系
式及诱导公式,三角函数的图象和性质,三角函数
的化简求值,三角形中的三角函数,三角函数的最
值及综合应用。一般设计一道或两道客观题,一
道解答题,约占总分的13%,即20分左右.多数是中、
低档题.近几年高考已逐步抛弃了对复杂三角变换
和特殊技巧的考查,而重点转移到对三角函数的
图象与性质的考查,对基础知识和基本技能的考查
上来.在考查三角公式进行恒等变形的同时,也直
接考查了三角函数的性质及图象的变换,降低了
对三角函数恒等变形的要求,加强了对三角函数
性质和图象的考查力度.
