高中数学人教B版必修4第一章基本初等函数(II)1.3.3已知三角函数求角课件
文档属性
| 名称 | 高中数学人教B版必修4第一章基本初等函数(II)1.3.3已知三角函数求角课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 540.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-20 00:00:00 | ||
图片预览








文档简介
课件27张PPT。已知三角函数值求角教学目标
知识目标
1.由三角函数值求角;
2.三角函数求值.
能力目标
1.会由已知的三角函数值求角;
2.会使用计算器求角.
德育目标
1.培养学生的应用意识;
2.培养学生的逻辑推理能力;
3.提高学生的解题能力;
4.培养学生的思维能力. 教学重点
由已知三角函数值求角 .
教学难点
1.根据[0,2π)范围确定有已知三角函数值的角 。
2.对函数arcsinx,arccosx,arctanx的正确认识。
3.用符号arcsinx,arccosx,arctanx表示所求的角。1.三角函数线
正弦、余弦、正切函数的图像与性质。知识链接已知一个角(定义域内),能求出它的一个三角函数值,
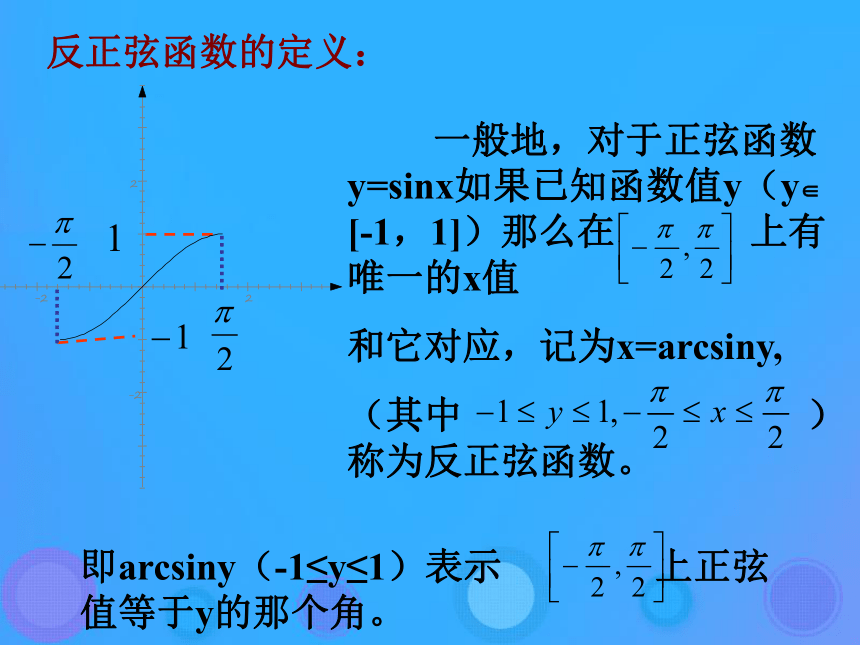
反之,已知一个三角函数值,如何求出与它对应的角?问题课前预习例1.已知正弦值,求角pQ 为使符合条件sinx=a (-1≤a ≤1)的角x 有且只有一个,选择:反正弦函数的定义: 一般地,对于正弦函数y=sinx如果已知函数值y(y∈ [-1,1])那么在 上有唯一的x值
和它对应,记为x=arcsiny,
(其中 )称为反正弦函数。 即arcsiny(-1≤y≤1)表示 上正弦值等于y的那个角。(1)定义域是[-1,1],值域
(2)sinα=b, α
arcsinb=α,b [-1,1]反正弦函数的性质:例2.(1)已知sinx=0.5,且
求x。(2)已知sinx=0.5,且x∈[0,2π]
求x。(3)已知sinx=-0.5,且x∈[0,2π]
求x。
(2)若,则x= (4)若 ,集合 且
,则x的值为 (3)若,则x=例 3( 1)已知 ,且 ,
求x ;
(2)已知 ,且 ,
求 x 的取值集合;
(3)已知 ,且 ,
求 x 的取值集合。2.已知余弦值和正切值,求角 为使符合条件cosx=a (-1≤a ≤1)
的角x 有且只有一个,选择:在区间[0,π]上符合条件cosx=y(-1≤y≤1)的角x,记x=arccosy。叫做y的反余弦。
(1)定义域是[-1,1],值域[0, ]
(2)cosα=b,
arcsinb=α,b [-1,1]反余弦函数的性质:练习2:(1)已知 , ,求x的取值集合.(2)已知 , ,求x的取值集合(3)若 ,则x的值( ) B
(1)定义域是______,值域_______
(2)tanα=b, a∈
arctanb=α,b∈ R反正切函数的性质:(1)若 ,则x的值( ) (2)若 ,集合 且
,则x的值为 B快乐体验 已知角x的一个三角函数值求角x,所得的角不一定只有一个,角的个数要根据角的取值范围来确定,这个范围在题目中是给定的.如果在这个范围内已知三角函数值的角不止一个,其解法可分为以下几个步骤:
(1)确定角x所在的象限;
(2)若函数值为正,先求出对应的锐角α;若函数值为负,先求出与函数值的绝对值对应的锐角α;
(3)根据x所在的象限,得出 0 ~ 2π间的角x:
若x在第一象限,则 x=α;若x在第二象限,则 x =π-α;
若x在第三象限,则 x=π+α;若x在第四象限,则 x =2π-α.
(4)如果要求适合条件的所有的角,则利用终边相同的角的表达式写出 .小 结:
知识目标
1.由三角函数值求角;
2.三角函数求值.
能力目标
1.会由已知的三角函数值求角;
2.会使用计算器求角.
德育目标
1.培养学生的应用意识;
2.培养学生的逻辑推理能力;
3.提高学生的解题能力;
4.培养学生的思维能力. 教学重点
由已知三角函数值求角 .
教学难点
1.根据[0,2π)范围确定有已知三角函数值的角 。
2.对函数arcsinx,arccosx,arctanx的正确认识。
3.用符号arcsinx,arccosx,arctanx表示所求的角。1.三角函数线
正弦、余弦、正切函数的图像与性质。知识链接已知一个角(定义域内),能求出它的一个三角函数值,
反之,已知一个三角函数值,如何求出与它对应的角?问题课前预习例1.已知正弦值,求角pQ 为使符合条件sinx=a (-1≤a ≤1)的角x 有且只有一个,选择:反正弦函数的定义: 一般地,对于正弦函数y=sinx如果已知函数值y(y∈ [-1,1])那么在 上有唯一的x值
和它对应,记为x=arcsiny,
(其中 )称为反正弦函数。 即arcsiny(-1≤y≤1)表示 上正弦值等于y的那个角。(1)定义域是[-1,1],值域
(2)sinα=b, α
arcsinb=α,b [-1,1]反正弦函数的性质:例2.(1)已知sinx=0.5,且
求x。(2)已知sinx=0.5,且x∈[0,2π]
求x。(3)已知sinx=-0.5,且x∈[0,2π]
求x。
(2)若,则x= (4)若 ,集合 且
,则x的值为 (3)若,则x=例 3( 1)已知 ,且 ,
求x ;
(2)已知 ,且 ,
求 x 的取值集合;
(3)已知 ,且 ,
求 x 的取值集合。2.已知余弦值和正切值,求角 为使符合条件cosx=a (-1≤a ≤1)
的角x 有且只有一个,选择:在区间[0,π]上符合条件cosx=y(-1≤y≤1)的角x,记x=arccosy。叫做y的反余弦。
(1)定义域是[-1,1],值域[0, ]
(2)cosα=b,
arcsinb=α,b [-1,1]反余弦函数的性质:练习2:(1)已知 , ,求x的取值集合.(2)已知 , ,求x的取值集合(3)若 ,则x的值( ) B
(1)定义域是______,值域_______
(2)tanα=b, a∈
arctanb=α,b∈ R反正切函数的性质:(1)若 ,则x的值( ) (2)若 ,集合 且
,则x的值为 B快乐体验 已知角x的一个三角函数值求角x,所得的角不一定只有一个,角的个数要根据角的取值范围来确定,这个范围在题目中是给定的.如果在这个范围内已知三角函数值的角不止一个,其解法可分为以下几个步骤:
(1)确定角x所在的象限;
(2)若函数值为正,先求出对应的锐角α;若函数值为负,先求出与函数值的绝对值对应的锐角α;
(3)根据x所在的象限,得出 0 ~ 2π间的角x:
若x在第一象限,则 x=α;若x在第二象限,则 x =π-α;
若x在第三象限,则 x=π+α;若x在第四象限,则 x =2π-α.
(4)如果要求适合条件的所有的角,则利用终边相同的角的表达式写出 .小 结:
