高中数学人教B版必修2第一章立体几何初步1.2.2空间中的平行关系(1)课件(18张)
文档属性
| 名称 | 高中数学人教B版必修2第一章立体几何初步1.2.2空间中的平行关系(1)课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-20 22:27:03 | ||
图片预览






文档简介
课件18张PPT。1.2.2空间中的平行关系(1)学习目标了解平行公理和空间角的关系定理。
能运用平行公理和空间角的关系定理证明一些有关空间直线位置关系的简单问题。一. 平行直线 1. 平行直线的定义:同一平面内不相交的两条直线叫做平行线. 2. 平行公理:过直线外一点有且只有一条直线和这条直线平行.3. 公理4:平行于同一直线的两条直线互相平行,此性质又叫做空间平行线的传递性.公理4的符号表述为:公理4反映了两条直线的位置关系.
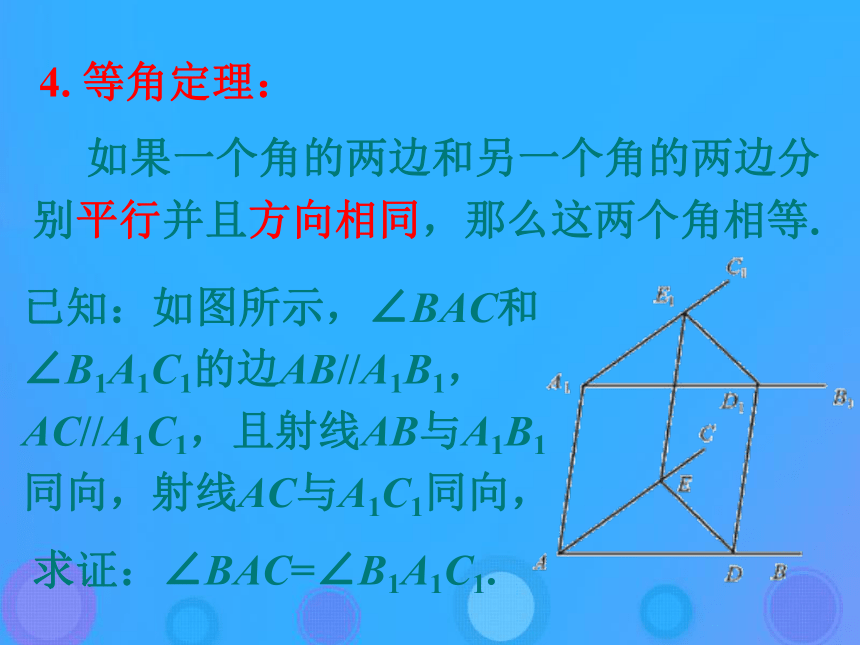
公理4主要用来证明两条直线平行,它是证明两直线平行的重要依据. 4. 等角定理: 如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.已知:如图所示,∠BAC和∠B1A1C1的边AB//A1B1,AC//A1C1,且射线AB与A1B1同向,射线AC与A1C1同向,求证:∠BAC=∠B1A1C1.证明:对于∠BAC和∠B1A1C1在同一个平面内的情形,在初中几何中已经证明, 下面证明两个角不在同一平面内的情形。 分别在∠BAC的两边和∠B1A1C1的两边上截取线段AD=A1D1和AE=A1E1. 所以DD1E1E是平行四边形。 在△ADE和△A1D1E1中. AD=A1D1,AE=A1E1,DE=D1E1, 于是△ADE≌△A1D1E1, 所以∠BAC=∠B1A1C1.5. 空间四边形的有关概念:(1)顺次连结不共面的四点A、B、C、D所构成的图形,叫做空间四边形;
(2)四个点中的各个点叫做空间四边形的顶点;
(3)所连结的相邻顶点间的线段叫做空间四边形的边;
(4)连结不相邻的顶点的线段叫做空间四边形的对角线。如图:空间四边形ABCD中,AC、BD是它的对角线 牛刀小试:1.如图,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD, A1D1的中点.
求证:∠C1E1B1 = ∠CEB.分析:设法证明E1C1∥EC, E1B1∥EB.1.空间两直线平行是指它们( )
A.无交点 B.共面且无交点
C.和同一条直线垂直 D.以上都不对 2.在空间,如果一个角的两边与另一个角的两边
分别平行,则这两个角( )
A.相等 B.互补
C.相等或互补 D.既不相等也不互补BC例1.已知:如图,空间四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形。证明:在△ABD中,因为E,H分别是AB,AD的中点,所以所以EH//FG,EH=FG,所以四边形EFGH是平行四边形。例2.如图:在长方体ABCD-A1B1C1D1中,已知E,F分别是AB , BC 的中点,
求证:EF∥A1C1.证明:连结AC.
在△ABC中, E, F分别是AB, BC 的中点.
所以 EF ∥ AC又因为 AA1∥BB1 且 AA1 = BB1
BB1∥CC1 且 BB1 = CC1所以 AA1=CC1 且 AA1∥CC1 即四边形AA1C1C是平行四边形所以AC∥A1C1从而 EF∥A1C1.1, 下列结论正确的是( )
A.若两个角相等,则这两个角的两边分别平行
B.空间四边形的四个顶点可以在一个平面内
C.空间四边形的两条对角线可以相交
D.空间四边形的两条对角线不相交D快乐体验 2,如图,已知在四面体ABCD中,AC=BD,
而且E,F,G,H分别为棱AB,BC,CD,DA的中点,求证:四边形EFGH是菱形。ABCDEHFG3若空间四边形的对角线相等,则以它的四条边的中点为顶点的四边形是( )
A.空间四边形 B.菱形
C.正方形 D.梯形B
能运用平行公理和空间角的关系定理证明一些有关空间直线位置关系的简单问题。一. 平行直线 1. 平行直线的定义:同一平面内不相交的两条直线叫做平行线. 2. 平行公理:过直线外一点有且只有一条直线和这条直线平行.3. 公理4:平行于同一直线的两条直线互相平行,此性质又叫做空间平行线的传递性.公理4的符号表述为:公理4反映了两条直线的位置关系.
公理4主要用来证明两条直线平行,它是证明两直线平行的重要依据. 4. 等角定理: 如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.已知:如图所示,∠BAC和∠B1A1C1的边AB//A1B1,AC//A1C1,且射线AB与A1B1同向,射线AC与A1C1同向,求证:∠BAC=∠B1A1C1.证明:对于∠BAC和∠B1A1C1在同一个平面内的情形,在初中几何中已经证明, 下面证明两个角不在同一平面内的情形。 分别在∠BAC的两边和∠B1A1C1的两边上截取线段AD=A1D1和AE=A1E1. 所以DD1E1E是平行四边形。 在△ADE和△A1D1E1中. AD=A1D1,AE=A1E1,DE=D1E1, 于是△ADE≌△A1D1E1, 所以∠BAC=∠B1A1C1.5. 空间四边形的有关概念:(1)顺次连结不共面的四点A、B、C、D所构成的图形,叫做空间四边形;
(2)四个点中的各个点叫做空间四边形的顶点;
(3)所连结的相邻顶点间的线段叫做空间四边形的边;
(4)连结不相邻的顶点的线段叫做空间四边形的对角线。如图:空间四边形ABCD中,AC、BD是它的对角线 牛刀小试:1.如图,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD, A1D1的中点.
求证:∠C1E1B1 = ∠CEB.分析:设法证明E1C1∥EC, E1B1∥EB.1.空间两直线平行是指它们( )
A.无交点 B.共面且无交点
C.和同一条直线垂直 D.以上都不对 2.在空间,如果一个角的两边与另一个角的两边
分别平行,则这两个角( )
A.相等 B.互补
C.相等或互补 D.既不相等也不互补BC例1.已知:如图,空间四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形。证明:在△ABD中,因为E,H分别是AB,AD的中点,所以所以EH//FG,EH=FG,所以四边形EFGH是平行四边形。例2.如图:在长方体ABCD-A1B1C1D1中,已知E,F分别是AB , BC 的中点,
求证:EF∥A1C1.证明:连结AC.
在△ABC中, E, F分别是AB, BC 的中点.
所以 EF ∥ AC又因为 AA1∥BB1 且 AA1 = BB1
BB1∥CC1 且 BB1 = CC1所以 AA1=CC1 且 AA1∥CC1 即四边形AA1C1C是平行四边形所以AC∥A1C1从而 EF∥A1C1.1, 下列结论正确的是( )
A.若两个角相等,则这两个角的两边分别平行
B.空间四边形的四个顶点可以在一个平面内
C.空间四边形的两条对角线可以相交
D.空间四边形的两条对角线不相交D快乐体验 2,如图,已知在四面体ABCD中,AC=BD,
而且E,F,G,H分别为棱AB,BC,CD,DA的中点,求证:四边形EFGH是菱形。ABCDEHFG3若空间四边形的对角线相等,则以它的四条边的中点为顶点的四边形是( )
A.空间四边形 B.菱形
C.正方形 D.梯形B
