高中数学人教B版必修3第一章算法初步1.1.3算法的三种基本逻辑结构课件(16张)
文档属性
| 名称 | 高中数学人教B版必修3第一章算法初步1.1.3算法的三种基本逻辑结构课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 442.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-20 22:38:54 | ||
图片预览




文档简介
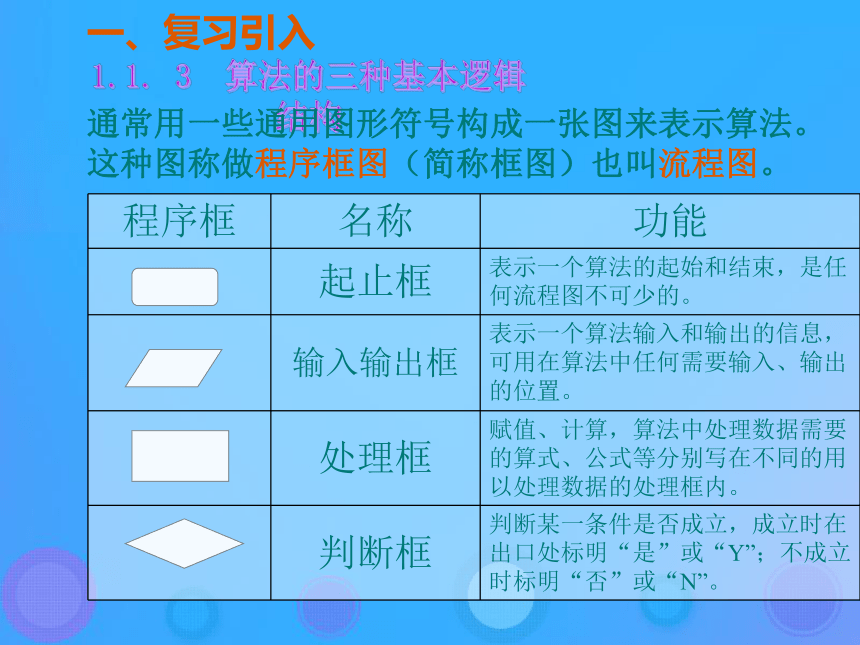
课件16张PPT。1.1. 3 算法的三种基本逻辑结构一、复习引入1.1. 3 算法的三种基本逻辑结构通常用一些通用图形符号构成一张图来表示算法。这种图称做程序框图(简称框图)也叫流程图。二、提出问题算法的基本逻辑结构 通过各式各样的算法和框图进行分析和研究,证明只须用顺序结构、条件分支结构和循环结构就可以表示任何一个算法。下面我们就系统地研究 我们写出的算法或画出的程序框图,一定要使大家一步步地看清楚、明白,容易阅读。不然的话,写得算法乱无头绪,就很难让人阅读和理解。这就要求算法或程序框图有一个良好的结构。三、概念形成概念1.顺序结构 顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构。
顺序结构在程序框图
中的体现就是用流程线将
程序框自上而下地连接起
来,按顺序执行算法步骤。步骤n步骤n+1三角形ABC的底BC为4, 高AD为2,求三角形ABC的面积S,试设计该问题的算法和流程。结束 开始计算 S=1/2ah输出S
输入a=4,h=2顺序结构三、概念形成概念1.顺序结构是是三、概念形成概念2.条件分支结构 在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向。条件结构就是处理这种过程的结构。
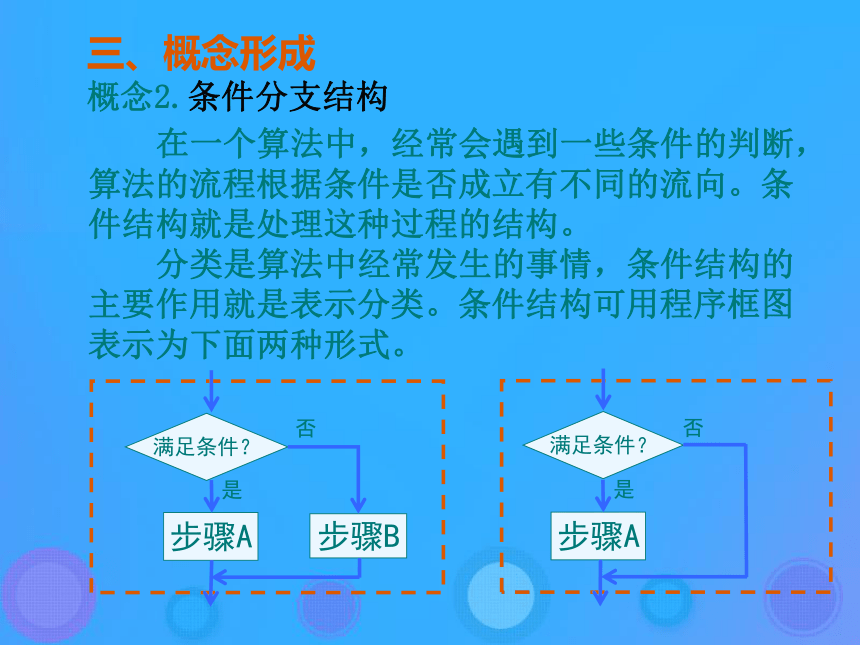
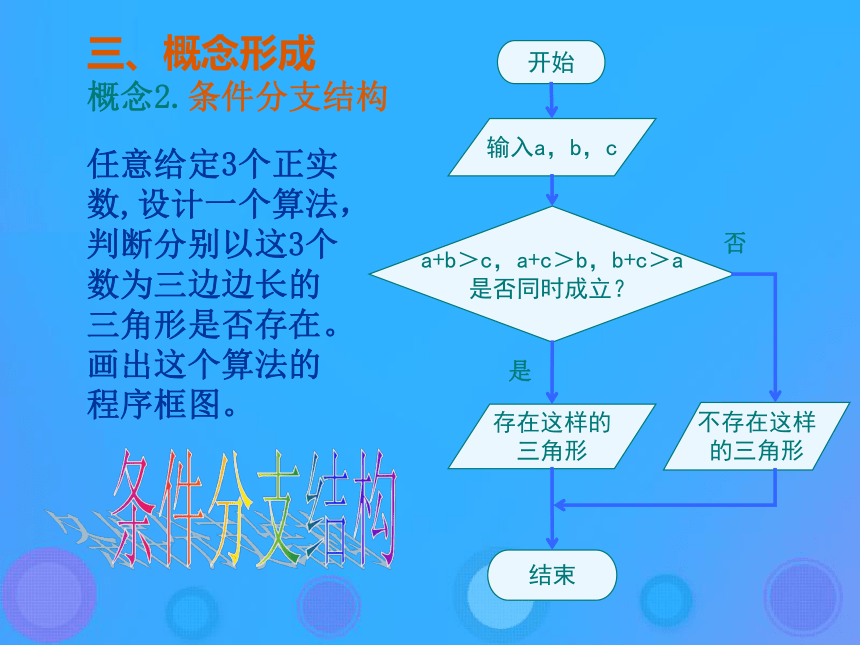
分类是算法中经常发生的事情,条件结构的主要作用就是表示分类。条件结构可用程序框图表示为下面两种形式。步骤A步骤B满足条件?否步骤A满足条件?否三、概念形成任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在。画出这个算法的程序框图。 概念2.条件分支结构开始输入a,b,ca+b>c,a+c>b,b+c>a
是否同时成立?存在这样的
三角形不存在这样
的三角形结束否是条件分支结构例1.已知点 和直线 ,求点
到直线 的距离 。四、应用举例解:(1)用数学语言来描述算法:S1:输入点的坐标 ,输入直线方程的系数A,B,C;S2:计算 ;S3:输出 ;S1:输入点的坐标,及直线系数: 例1.已知点 和直线 ,求点
到直线 的距离 。四、应用举例解:(2)用框图来描述算法:开始输入结束S2:计算:S3:输出 ;例2.设火车托运 行李时,每千米的费用(单位:元)标准为:四、应用举例解:先输入托运重量为P和里程D,再分别用各自条件下的计算式子来进行计算处理,然后将结果与托运路程D想成,最后输出托运行李费用M。画出行李托运费用的程序框图。例3.写出下列程序框图的运行结果。四、应用举例(1)运行结果 。例3.写出下列程序框图的运行结果。四、应用举例(2)当x输入,-2,0,2时运行结果
分别是 。开始输入x输出y结束例3.写出下列程序框图的运行结果。四、应用举例(3)已知函数 ,程序框图表示的是给出x值,求相应的函数值的算法。将框图补充完整。其中①处应填写 ;②处应填写 。算法课堂练习1.如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,用流程图表示这一算法的过程。算法课堂练习2.下面的流程图表示了一个什么样的算法? 所给流程图描述了求三个数a,b,c的最大数的算法。算法课堂练习3.下边的程序框图(如图所示),能判断任意输入的数x的奇偶性,其中判断框内的条件是( )
A. m=0 B. x=0
C. x=1 D. m=1A
顺序结构在程序框图
中的体现就是用流程线将
程序框自上而下地连接起
来,按顺序执行算法步骤。步骤n步骤n+1三角形ABC的底BC为4, 高AD为2,求三角形ABC的面积S,试设计该问题的算法和流程。结束 开始计算 S=1/2ah输出S
输入a=4,h=2顺序结构三、概念形成概念1.顺序结构是是三、概念形成概念2.条件分支结构 在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向。条件结构就是处理这种过程的结构。
分类是算法中经常发生的事情,条件结构的主要作用就是表示分类。条件结构可用程序框图表示为下面两种形式。步骤A步骤B满足条件?否步骤A满足条件?否三、概念形成任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在。画出这个算法的程序框图。 概念2.条件分支结构开始输入a,b,ca+b>c,a+c>b,b+c>a
是否同时成立?存在这样的
三角形不存在这样
的三角形结束否是条件分支结构例1.已知点 和直线 ,求点
到直线 的距离 。四、应用举例解:(1)用数学语言来描述算法:S1:输入点的坐标 ,输入直线方程的系数A,B,C;S2:计算 ;S3:输出 ;S1:输入点的坐标,及直线系数: 例1.已知点 和直线 ,求点
到直线 的距离 。四、应用举例解:(2)用框图来描述算法:开始输入结束S2:计算:S3:输出 ;例2.设火车托运 行李时,每千米的费用(单位:元)标准为:四、应用举例解:先输入托运重量为P和里程D,再分别用各自条件下的计算式子来进行计算处理,然后将结果与托运路程D想成,最后输出托运行李费用M。画出行李托运费用的程序框图。例3.写出下列程序框图的运行结果。四、应用举例(1)运行结果 。例3.写出下列程序框图的运行结果。四、应用举例(2)当x输入,-2,0,2时运行结果
分别是 。开始输入x输出y结束例3.写出下列程序框图的运行结果。四、应用举例(3)已知函数 ,程序框图表示的是给出x值,求相应的函数值的算法。将框图补充完整。其中①处应填写 ;②处应填写 。算法课堂练习1.如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,用流程图表示这一算法的过程。算法课堂练习2.下面的流程图表示了一个什么样的算法? 所给流程图描述了求三个数a,b,c的最大数的算法。算法课堂练习3.下边的程序框图(如图所示),能判断任意输入的数x的奇偶性,其中判断框内的条件是( )
A. m=0 B. x=0
C. x=1 D. m=1A
