数学人教B版必修2第二章平面解析几何初步2.2.1直线方程的几种形式课件(24张PPT)
文档属性
| 名称 | 数学人教B版必修2第二章平面解析几何初步2.2.1直线方程的几种形式课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 297.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-21 09:53:41 | ||
图片预览








文档简介
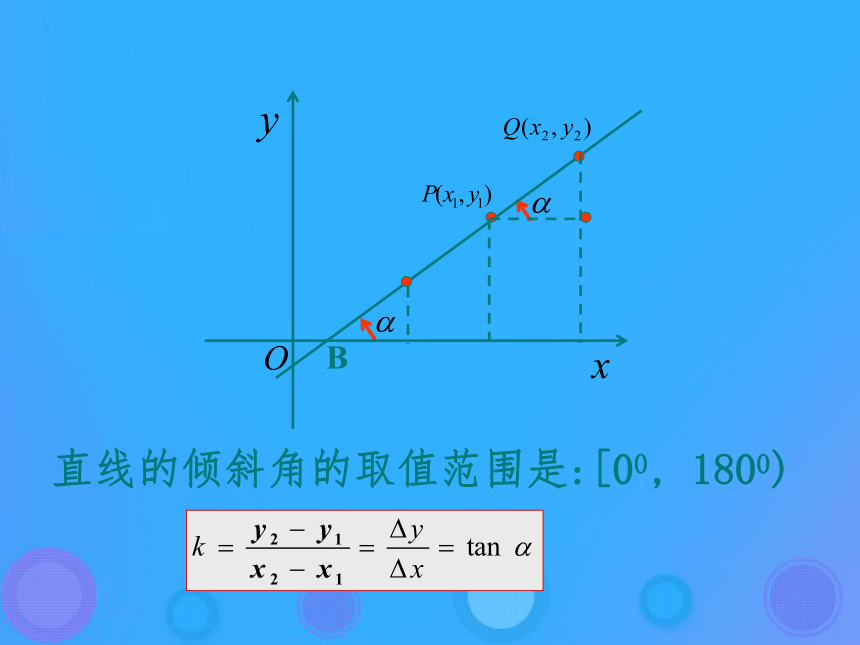
课件24张PPT。2.2.2 直线的点斜式方程复习1.倾斜角 的定义及其取值范围;直线的倾斜角的取值范围是:[00, 1800)B 在平面直角坐标系内,如果给定一条直线 经过的一个点 和斜率 ,能否将直线上所有的点的坐标 满足的关系表示出来呢?问题引入 直线经过点 ,且斜率为 ,设点 是直线上不同于点 的任意一点,因为直线 的斜率为 ,由斜率公式得:即:问题引入 (1)过点 ,斜率是 的直线 上的点,其坐标都满足方程 吗? (2)坐标满足方程 的点都在过点 ,斜率为 的直线 上吗? 经过探究,上述两条都成立,所以这个方程就是过点 ,斜率为 的直线 的方程.概念理解 方程 由直线上一点及其斜率确定,把这个方程叫做直线的点斜式方程,简称点斜式(point slope form).直线的点斜式方程 (1) 轴所在直线的方程是什么?,或 当直线 的倾斜角为 时,即 .这时直线 与 轴平行或重合,的方程就是坐标轴的直线方程 故 轴所在直线的方程是: (2) 轴所在直线的方程是什么?,或 当直线 的倾斜角为 时,直线没有斜率,这时直线 与 轴平行或重合,它的方程不能用点斜式表示.这时,直线 上每一点的横坐标都等于 ,所以它的方程就是坐标轴的直线方程 故 轴所在直线的方程是:牛刀小试求下列直线的方程: 如果直线 的斜率为 ,且与 轴的交点为 ,代入直线的点斜式方程,得: 也就是:xyOlb 我们把直线与 轴交点的纵坐标b叫做直线在轴上的截距(intercept). 该方程由直线的斜率与它在 轴上的截距确定,所以该方程叫做直线的斜截式方程,简称斜截式(slope intercept form).直线的斜截式方程 观察方程 ,它的形式具有什么特点? 1、我们发现,左端 的系数恒为1,右端 的系数
和常数项 均有明显的几何意义:问题引入2、斜截式是点斜式的特例,只适用于斜率存在的情形。 3、直线在坐标轴上的横、纵截距及求法:
截距的值是实数,它是坐标值,不是距离4、 方程 与我们学过的一次函数的表达式类似.我们知道,一次函数的图象是一条直线.你如何从直线方程的角度认识一次函数 ?一次函数中 和 的几何意义是什么? 5、你能说出一次函数 及 图象的特点吗?问题引入牛刀小试思考:大家都知道:两点确定一条直线!
那么经过两个定点的直线的方程能否用“公式”直接写出来呢?二、问题的提出: 三、师生探究(一):直线的两点式方程 合作学习1 : 设直线l经过两点P1(x1,y1),P2(x2,y2),其中 x1≠x2,y1≠y2,
则①直线l斜率是什么?
②你能写出直线l的点斜式方程吗?
结论: (1)斜率
(2)方程
写成比例式可化为_____________. 设直线l经过两点P1(x1,y1), P2(x2,y2),
其中 x1≠x2,y1≠y2,求l的方程.展示:展示: 设直线l经过两点P1(x1,y1), P2(x2,y2),
其中 x1≠x2,y1≠y2,求l的方程.
结论: 方程
化成比例式为 :
(x1≠x2且y1≠y2)
此方程叫做直线的两点式方程。说明(1)这个方程由直线上两点确定;
(2)当直线没有斜率或斜率为0时,不能用
两点式求出它们的方程.(此时方程如何得到?)典例分析1: 已知三角形的三个顶点
A(-4,0),B(2,-4),C(0,2),
求AC边所在直线的方程,以及BC边上中线
所在直线的方程。练习B练习根据下列条件,求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2;
和常数项 均有明显的几何意义:问题引入2、斜截式是点斜式的特例,只适用于斜率存在的情形。 3、直线在坐标轴上的横、纵截距及求法:
截距的值是实数,它是坐标值,不是距离4、 方程 与我们学过的一次函数的表达式类似.我们知道,一次函数的图象是一条直线.你如何从直线方程的角度认识一次函数 ?一次函数中 和 的几何意义是什么? 5、你能说出一次函数 及 图象的特点吗?问题引入牛刀小试思考:大家都知道:两点确定一条直线!
那么经过两个定点的直线的方程能否用“公式”直接写出来呢?二、问题的提出: 三、师生探究(一):直线的两点式方程 合作学习1 : 设直线l经过两点P1(x1,y1),P2(x2,y2),其中 x1≠x2,y1≠y2,
则①直线l斜率是什么?
②你能写出直线l的点斜式方程吗?
结论: (1)斜率
(2)方程
写成比例式可化为_____________. 设直线l经过两点P1(x1,y1), P2(x2,y2),
其中 x1≠x2,y1≠y2,求l的方程.展示:展示: 设直线l经过两点P1(x1,y1), P2(x2,y2),
其中 x1≠x2,y1≠y2,求l的方程.
结论: 方程
化成比例式为 :
(x1≠x2且y1≠y2)
此方程叫做直线的两点式方程。说明(1)这个方程由直线上两点确定;
(2)当直线没有斜率或斜率为0时,不能用
两点式求出它们的方程.(此时方程如何得到?)典例分析1: 已知三角形的三个顶点
A(-4,0),B(2,-4),C(0,2),
求AC边所在直线的方程,以及BC边上中线
所在直线的方程。练习B练习根据下列条件,求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2;
