数学人教B版必修3第一章算法初步1.3中国古代数学中的算法案例课件(28张PPT)
文档属性
| 名称 | 数学人教B版必修3第一章算法初步1.3中国古代数学中的算法案例课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 496.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-21 09:54:49 | ||
图片预览





文档简介
课件28张PPT。1.3 中国古代数学中的算法案例第一章 算法初步一、复习引入 下面我们举一些我国古代代数学中“算法”的例子,让同学们体会“算法”的概念,看一看中国古代数学在算法上的伟大成就。 我们在小学、中学学到的算术、代数,从计数到多元一次联立方程组以及方程的求根方法,都是我国古代数学家最先创造的,有的比其他国家早几百年甚至上千年。我国人民在长期的生活、生产和劳动中,创造了很多数学的计算和思想方法。二、提出问题本节主要介绍的内容一、更相减损之术(又称“等值算法”)
----研究如何求二个正整数的最大公约数。二、割圆术
----解决圆周率π的近似值问题。三、秦九韶算法
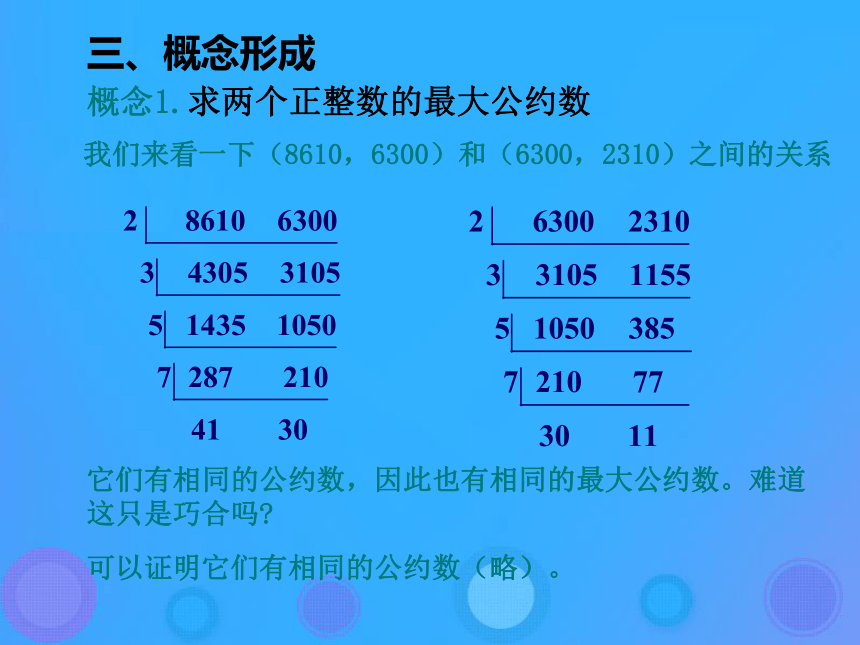
----解决求多项式函数值问题。三、概念形成概念1.求两个正整数的最大公约数你记得在小学里是如何求最大公约数吗?对了,用短除法。例如求18和30的最大公约数:所以,18与30的最大公约数是2×3=6。 这个方法可以总结为:用两个数连续除以他们的公约数,一直除到所得的商是互质数为止,然后把所有的除数连乘起来。三、概念形成概念1.求两个正整数的最大公约数 当两个数比较大时(如8610与6300),使用上述方法求最大公约数就比较困难。下面我们介绍两种古老而有效的算法——辗转相除法与更相减损术。(1)辗转相除法(*)例子:辗转相除法求8610和6300的最大公约数。为了简洁,我们把8610和6300的最大公约数记作(8610,6300)。把8610变为下式 8610 = 6300×1 + 2310 三、概念形成概念1.求两个正整数的最大公约数我们来看一下(8610,6300)和(6300,2310)之间的关系 它们有相同的公约数,因此也有相同的最大公约数。难道这只是巧合吗? 可以证明它们有相同的公约数(略)。 三、概念形成我们可以总结为:
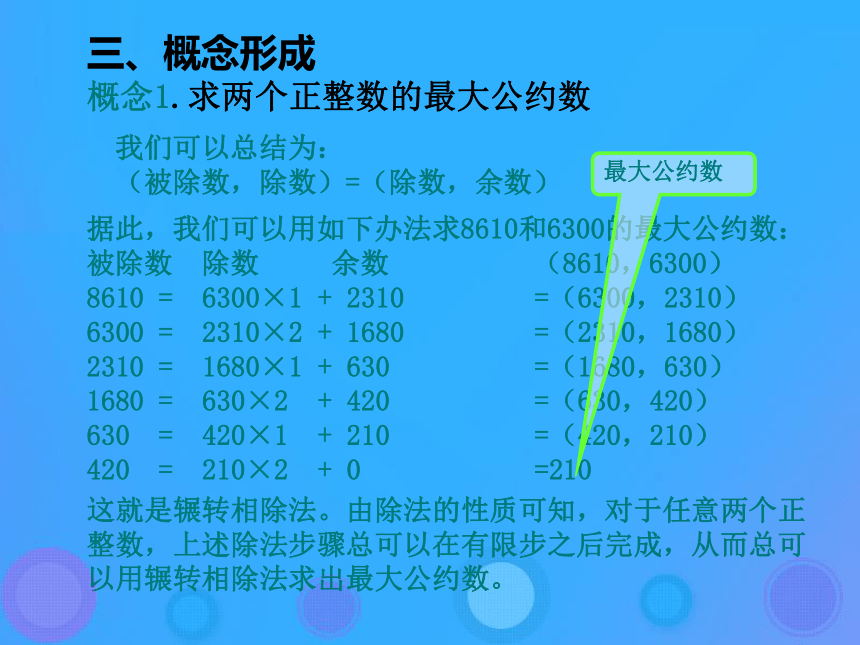
(被除数,除数)=(除数,余数)概念1.求两个正整数的最大公约数据此,我们可以用如下办法求8610和6300的最大公约数:
被除数 除数 余数 (8610,6300)
8610 = 6300×1 + 2310 =(6300,2310)
6300 = 2310×2 + 1680 =(2310,1680)
2310 = 1680×1 + 630 =(1680,630)
1680 = 630×2 + 420 =(630,420)
630 = 420×1 + 210 =(420,210)
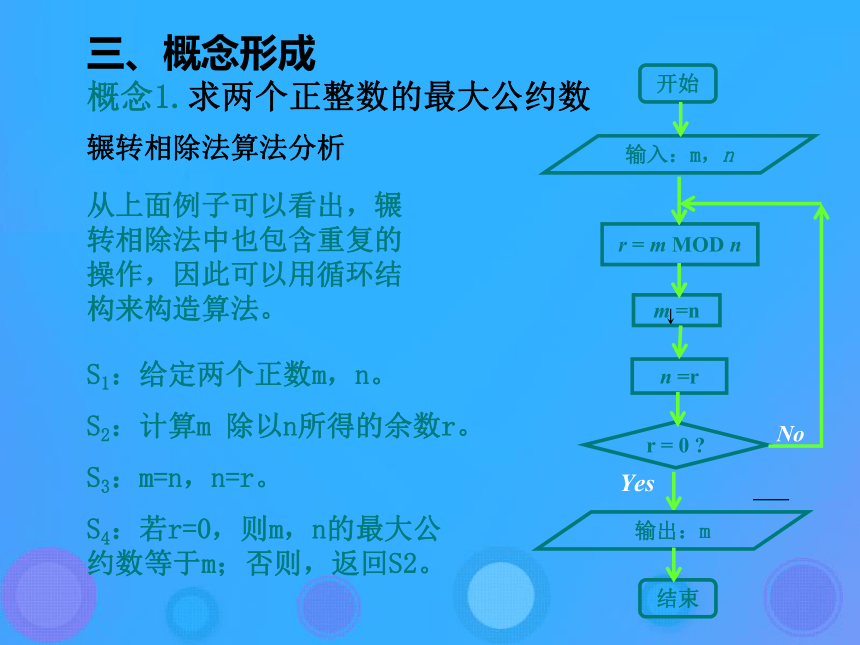
420 = 210×2 + 0 =210最大公约数这就是辗转相除法。由除法的性质可知,对于任意两个正整数,上述除法步骤总可以在有限步之后完成,从而总可以用辗转相除法求出最大公约数。 三、概念形成辗转相除法算法分析概念1.求两个正整数的最大公约数从上面例子可以看出,辗转相除法中也包含重复的操作,因此可以用循环结构来构造算法。S1:给定两个正数m,n。
S2:计算m 除以n所得的余数r。
S3:m=n,n=r。
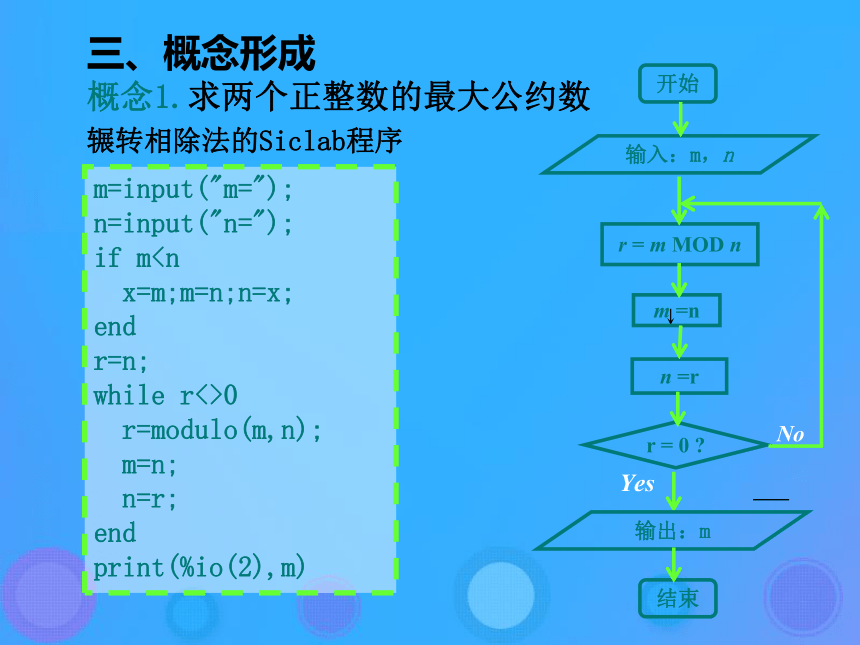
S4:若r=0,则m,n的最大公约数等于m;否则,返回S2。r = 0 ? n =rm =nr = m MOD n输入:m,n输出:m开始结束三、概念形成辗转相除法的Siclab程序概念1.求两个正整数的最大公约数m=input("m=");
n=input("n=");
if m x=m;m=n;n=x;
end
r=n;
while r<>0
r=modulo(m,n);
m=n;
n=r;
end
print(%io(2),m)三、概念形成概念1.求两个正整数的最大公约数(2)更相减损术《九章算术》是中国古代的数学专著,其中有这样一段论述:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。”。这是一个求最简分式的算法,可以用它来求最大公约数, 我们称为“更相减损术”。 翻译为现代语言如下 三、概念形成概念1.求两个正整数的最大公约数(2)更相减损术第一步:任意给两个正整数,如果它们都是偶数,用2约简;若不是,执行第二步。 第二步:以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到它们相等为止,则这个“相等的数”就是所求的最大公约数;如果操作过程中有约分,还要在“等数”上乘以约掉的因数。三、概念形成概念1.求两个正整数的最大公约数(2)更相减损术例如:求78和36的最大公约数。解:(78,36)(6,36)(42,36)(6,30)(6,18)(6,12)(6,24)(6,6)所以,78和36的最大公约数为6。此种算法称为“等值算法”。三、概念形成概念1.求两个正整数的最大公约数m=input("m=");
n=input("n=");
while m<>n
if m>n
m=m-n;
else
n=n-m;
end
end
print(%io(2),m,n);(2)更相减损术三、概念形成概念2.割圆术 所谓“割圆术”,是用圆内接正多边形的周长去无限逼近圆周并以此求取圆周率的方法。这个方法,是我国魏晋时期刘徽在批判总结了数学史上各种旧的计算方法之后,经过深思熟虑才创造出来的一种崭新的方法。 刘徽从圆内接正六边形把圆周等分为六条弧的基础上,再继续等分,把每段弧再分割为二,做出一个圆内接正十二边形,这个正十二边形的周长不就要比正六边形的周长更接近圆周了吗?如果把圆周再继续分割,做成一个圆内接正二十四边形,那么这个正二十四边形的周长必然又比正十二边形的周长更接近圆周。三、概念形成概念2.割圆术先分析割圆术的算法1hnxn设圆o的面积为S,其内接正n边形的面积为Sn.所以正2n边形的面积等于:S2n=Sn+n·xn(1-hn)/2.从而有S2n<S<S2n+(S2n-Sn).计算圆周率的不足近似值计算圆周率的过剩近似值由于三、概念形成概念2.割圆术1hnxn割圆术的Siclab程序n=6;
x=1;
s=6*sqrt(3)/4;
for i=1:1:5
h=sqrt(1-(x/2)^2);
s=s+n*x*(1-h)/2;
n=2*n;
x=sqrt((x/2)^2+(1-h)^2);
end
print(%io(2),n,s);由于三、概念形成概念3.秦九韶算法已知 求当 时的函数值,要用多少次乘法,多少次加法? 乘法:4+3+2+1= 。
加法: 。乘法和加法的次数能减少吗? 聪明的同学们一定想到了,如果我们计算出了x2,当我们计算x3时根本不用从头算起,利用x2用一次乘法就可以算出x3了。同理x4可由x3算出,x5可由x4算出,这样我们只用了4次乘法即可。计算过程大大简化。对于计算机来说,做一次乘法运算所用的时间比一次加法运算要长的多,所以减少乘法运算次数,计算机能更快的得到结果。 三、概念形成概念3.秦九韶算法比如一个5次多项式为 求当 时的函数值,要用多少次乘法,多少次加法? 还有更快速的算法吗?分析:用刚才的方法,计算 共用4次乘法,乘上它们的系数需要5次乘法,共需要9次乘法和5次加法。三、概念形成概念3.秦九韶算法比如一个5次多项式为 求当 时的函数值,要用多少次乘法,多少次加法? 解:原式可化为多项式的系数分别为:先计算最内层括号里 的值,然后由内向外逐层计算。三、概念形成概念3.秦九韶算法比如一个5次多项式为 求当 时的函数值,要用多少次乘法,多少次加法? 多项式的系数分别为:共用了5次乘法和5次加法,减少了4次乘法。三、概念形成概念3.秦九韶算法用秦九韶算法求n次多项式的值时,需要n次乘法运算,n次加法运算,共2n次运算。三、概念形成概念3.秦九韶算法开始结束i=i-1 i=n-1输出v输入n,an,x输入ain=input("n=");
an=input("an=");
x=input("x=");
v=an;
i=n-1;
while i>=0
print(%io(2),i)
a=input("ai=");
v=v*x+a;i=i-1;
end
print(%io(2),v)用秦九韶算法框图及程序四、应用举例例1.用更相减损术求132与143的最大公约数(132,143)(132,11)(121,11)(110,11)(99,11)(88,11)(77,11)(66,11)(55,11)(44,11)(33,11)(22,11)(11,11)故,132与143的最大公约数是11。思考:用辗转相除法求下列两数的最大公约数。
(1)8251,6105 (2)1480,480四、应用举例例2.用秦九韶算法求多项式 在x=2时的函数值。 算法程序可参照前面的秦九韶算法程序。五、课堂练习1、用秦九韶算法求多项式f(x)=2+0.35x+1.8x2-3.66x3+6x4-5.2x5+x6在x=-1.3的值时,令v0=a6;v1=v0x+a5; …;v6=v5x+a0时,v3的值为( )
A.-9.8205 B.14.25 C.-22.445 D.30.9785 C2.数4557、1953、5115的最大公约数是( )
A.31 B.93 C.217 D.651B3.用等值算法求下列各数的最大公约数.
(1)63,84; (2)351,513.答案:(1)21 (2)274.用辗转相除法求下列各数的最大公约数.
(1)5207,8323;(2)5671,10759.答案:(1)41 (2) 53
6.用秦九韶算法求多项式 在 时的值.5.求三个数779,209,589的最大公约数.144468 19六、课堂总结①重点是理解中国古代的三个问题的算法,难点是为算法编写程序。②理解并掌握更相减损术求两个正整数的最大公约数的步骤及秦九韶算法的计算过程。
----研究如何求二个正整数的最大公约数。二、割圆术
----解决圆周率π的近似值问题。三、秦九韶算法
----解决求多项式函数值问题。三、概念形成概念1.求两个正整数的最大公约数你记得在小学里是如何求最大公约数吗?对了,用短除法。例如求18和30的最大公约数:所以,18与30的最大公约数是2×3=6。 这个方法可以总结为:用两个数连续除以他们的公约数,一直除到所得的商是互质数为止,然后把所有的除数连乘起来。三、概念形成概念1.求两个正整数的最大公约数 当两个数比较大时(如8610与6300),使用上述方法求最大公约数就比较困难。下面我们介绍两种古老而有效的算法——辗转相除法与更相减损术。(1)辗转相除法(*)例子:辗转相除法求8610和6300的最大公约数。为了简洁,我们把8610和6300的最大公约数记作(8610,6300)。把8610变为下式 8610 = 6300×1 + 2310 三、概念形成概念1.求两个正整数的最大公约数我们来看一下(8610,6300)和(6300,2310)之间的关系 它们有相同的公约数,因此也有相同的最大公约数。难道这只是巧合吗? 可以证明它们有相同的公约数(略)。 三、概念形成我们可以总结为:
(被除数,除数)=(除数,余数)概念1.求两个正整数的最大公约数据此,我们可以用如下办法求8610和6300的最大公约数:
被除数 除数 余数 (8610,6300)
8610 = 6300×1 + 2310 =(6300,2310)
6300 = 2310×2 + 1680 =(2310,1680)
2310 = 1680×1 + 630 =(1680,630)
1680 = 630×2 + 420 =(630,420)
630 = 420×1 + 210 =(420,210)
420 = 210×2 + 0 =210最大公约数这就是辗转相除法。由除法的性质可知,对于任意两个正整数,上述除法步骤总可以在有限步之后完成,从而总可以用辗转相除法求出最大公约数。 三、概念形成辗转相除法算法分析概念1.求两个正整数的最大公约数从上面例子可以看出,辗转相除法中也包含重复的操作,因此可以用循环结构来构造算法。S1:给定两个正数m,n。
S2:计算m 除以n所得的余数r。
S3:m=n,n=r。
S4:若r=0,则m,n的最大公约数等于m;否则,返回S2。r = 0 ? n =rm =nr = m MOD n输入:m,n输出:m开始结束三、概念形成辗转相除法的Siclab程序概念1.求两个正整数的最大公约数m=input("m=");
n=input("n=");
if m
end
r=n;
while r<>0
r=modulo(m,n);
m=n;
n=r;
end
print(%io(2),m)三、概念形成概念1.求两个正整数的最大公约数(2)更相减损术《九章算术》是中国古代的数学专著,其中有这样一段论述:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。”。这是一个求最简分式的算法,可以用它来求最大公约数, 我们称为“更相减损术”。 翻译为现代语言如下 三、概念形成概念1.求两个正整数的最大公约数(2)更相减损术第一步:任意给两个正整数,如果它们都是偶数,用2约简;若不是,执行第二步。 第二步:以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到它们相等为止,则这个“相等的数”就是所求的最大公约数;如果操作过程中有约分,还要在“等数”上乘以约掉的因数。三、概念形成概念1.求两个正整数的最大公约数(2)更相减损术例如:求78和36的最大公约数。解:(78,36)(6,36)(42,36)(6,30)(6,18)(6,12)(6,24)(6,6)所以,78和36的最大公约数为6。此种算法称为“等值算法”。三、概念形成概念1.求两个正整数的最大公约数m=input("m=");
n=input("n=");
while m<>n
if m>n
m=m-n;
else
n=n-m;
end
end
print(%io(2),m,n);(2)更相减损术三、概念形成概念2.割圆术 所谓“割圆术”,是用圆内接正多边形的周长去无限逼近圆周并以此求取圆周率的方法。这个方法,是我国魏晋时期刘徽在批判总结了数学史上各种旧的计算方法之后,经过深思熟虑才创造出来的一种崭新的方法。 刘徽从圆内接正六边形把圆周等分为六条弧的基础上,再继续等分,把每段弧再分割为二,做出一个圆内接正十二边形,这个正十二边形的周长不就要比正六边形的周长更接近圆周了吗?如果把圆周再继续分割,做成一个圆内接正二十四边形,那么这个正二十四边形的周长必然又比正十二边形的周长更接近圆周。三、概念形成概念2.割圆术先分析割圆术的算法1hnxn设圆o的面积为S,其内接正n边形的面积为Sn.所以正2n边形的面积等于:S2n=Sn+n·xn(1-hn)/2.从而有S2n<S<S2n+(S2n-Sn).计算圆周率的不足近似值计算圆周率的过剩近似值由于三、概念形成概念2.割圆术1hnxn割圆术的Siclab程序n=6;
x=1;
s=6*sqrt(3)/4;
for i=1:1:5
h=sqrt(1-(x/2)^2);
s=s+n*x*(1-h)/2;
n=2*n;
x=sqrt((x/2)^2+(1-h)^2);
end
print(%io(2),n,s);由于三、概念形成概念3.秦九韶算法已知 求当 时的函数值,要用多少次乘法,多少次加法? 乘法:4+3+2+1= 。
加法: 。乘法和加法的次数能减少吗? 聪明的同学们一定想到了,如果我们计算出了x2,当我们计算x3时根本不用从头算起,利用x2用一次乘法就可以算出x3了。同理x4可由x3算出,x5可由x4算出,这样我们只用了4次乘法即可。计算过程大大简化。对于计算机来说,做一次乘法运算所用的时间比一次加法运算要长的多,所以减少乘法运算次数,计算机能更快的得到结果。 三、概念形成概念3.秦九韶算法比如一个5次多项式为 求当 时的函数值,要用多少次乘法,多少次加法? 还有更快速的算法吗?分析:用刚才的方法,计算 共用4次乘法,乘上它们的系数需要5次乘法,共需要9次乘法和5次加法。三、概念形成概念3.秦九韶算法比如一个5次多项式为 求当 时的函数值,要用多少次乘法,多少次加法? 解:原式可化为多项式的系数分别为:先计算最内层括号里 的值,然后由内向外逐层计算。三、概念形成概念3.秦九韶算法比如一个5次多项式为 求当 时的函数值,要用多少次乘法,多少次加法? 多项式的系数分别为:共用了5次乘法和5次加法,减少了4次乘法。三、概念形成概念3.秦九韶算法用秦九韶算法求n次多项式的值时,需要n次乘法运算,n次加法运算,共2n次运算。三、概念形成概念3.秦九韶算法开始结束i=i-1 i=n-1输出v输入n,an,x输入ain=input("n=");
an=input("an=");
x=input("x=");
v=an;
i=n-1;
while i>=0
print(%io(2),i)
a=input("ai=");
v=v*x+a;i=i-1;
end
print(%io(2),v)用秦九韶算法框图及程序四、应用举例例1.用更相减损术求132与143的最大公约数(132,143)(132,11)(121,11)(110,11)(99,11)(88,11)(77,11)(66,11)(55,11)(44,11)(33,11)(22,11)(11,11)故,132与143的最大公约数是11。思考:用辗转相除法求下列两数的最大公约数。
(1)8251,6105 (2)1480,480四、应用举例例2.用秦九韶算法求多项式 在x=2时的函数值。 算法程序可参照前面的秦九韶算法程序。五、课堂练习1、用秦九韶算法求多项式f(x)=2+0.35x+1.8x2-3.66x3+6x4-5.2x5+x6在x=-1.3的值时,令v0=a6;v1=v0x+a5; …;v6=v5x+a0时,v3的值为( )
A.-9.8205 B.14.25 C.-22.445 D.30.9785 C2.数4557、1953、5115的最大公约数是( )
A.31 B.93 C.217 D.651B3.用等值算法求下列各数的最大公约数.
(1)63,84; (2)351,513.答案:(1)21 (2)274.用辗转相除法求下列各数的最大公约数.
(1)5207,8323;(2)5671,10759.答案:(1)41 (2) 53
6.用秦九韶算法求多项式 在 时的值.5.求三个数779,209,589的最大公约数.144468 19六、课堂总结①重点是理解中国古代的三个问题的算法,难点是为算法编写程序。②理解并掌握更相减损术求两个正整数的最大公约数的步骤及秦九韶算法的计算过程。
