人教版2018-2019学年初中数学7年级下《5.1 相交线》同步练习题(含答案)
文档属性
| 名称 | 人教版2018-2019学年初中数学7年级下《5.1 相交线》同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 126.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-21 12:59:53 | ||
图片预览


文档简介
人教版2019学年初中数学7年级下《5.1 相交线》同步练习题
评卷人 得 分
一.选择题(共10小题)
1.任意画三条直线,交点的个数是( )
A.1 B.1或3 C.0或1或2或3 D.不能确定
2.平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.16 B.18 C.29 D.28
3.下列说法正确的是( )
(1)如果∠1+∠2+∠3=180°,那么∠1与∠2与∠3互为补角;
(2)如果∠A+∠B=90°,那么∠A是余角;
(3)互为补角的两个角的平分线互相垂直;
(4)有公共顶点且又相等的角是对顶角;
(5)如果两个角相等,那么它们的余角也相等.
A.1个 B.2个 C.3个 D.4个
4.如图所示,直线AB和CD相交于点O,则∠AOC与∠BOD的关系是( )
A.∠AOC=∠BOD B.∠AOC<∠BOD C.∠AOC>∠BOD D.不确定
5.有下列说法:
①两条直线相交成四个角,如果两个角相等,那么这两条直线垂直;
②两条直线相交成四个角,如果三个角相等,那么这两条直线垂直;
③在同一平面内,过直线上一点可以作无数条直线与已知直线垂直;
④直线外一点到这条的垂线段,叫做点到直线的距离.
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
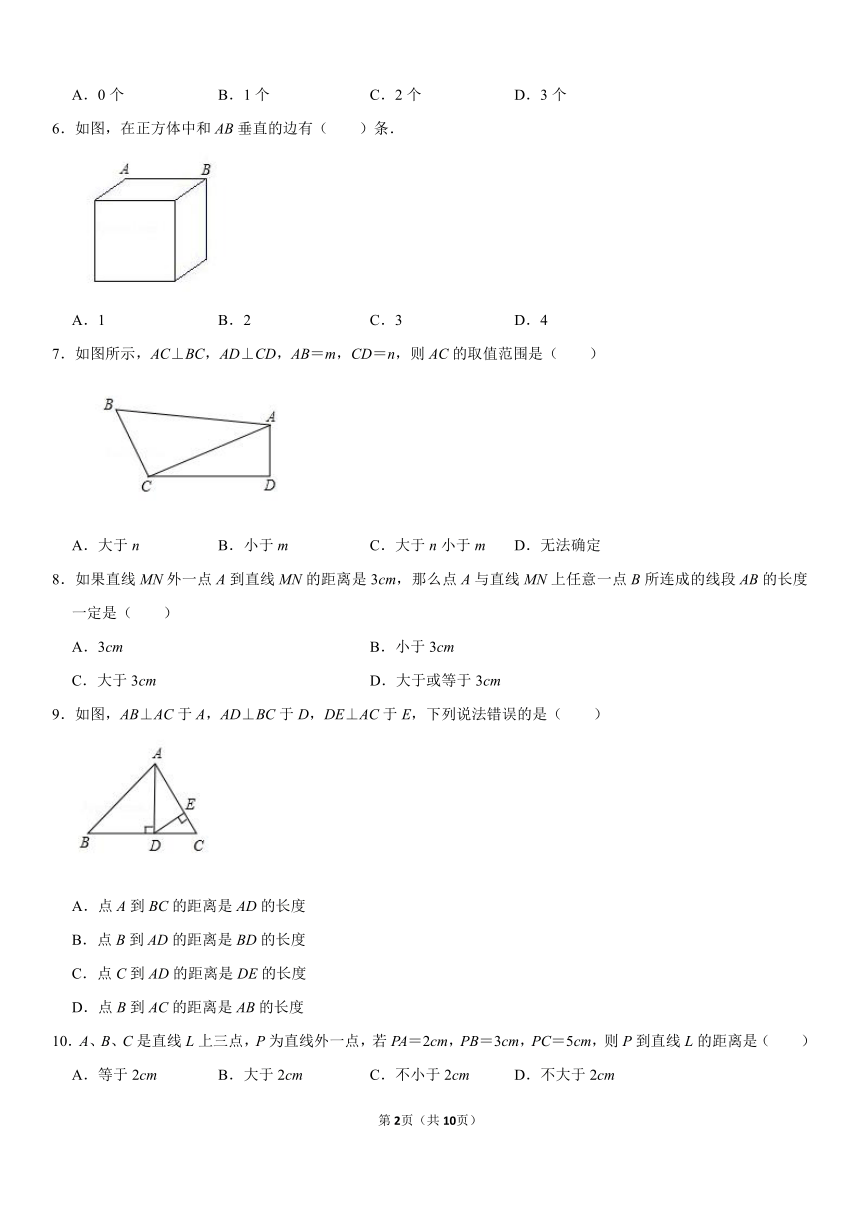
6.如图,在正方体中和AB垂直的边有( )条.
A.1 B.2 C.3 D.4
7.如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC的取值范围是( )
A.大于n B.小于m C.大于n小于m D.无法确定
8.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm B.小于3cm
C.大于3cm D.大于或等于3cm
9.如图,AB⊥AC于A,AD⊥BC于D,DE⊥AC于E,下列说法错误的是( )
A.点A到BC的距离是AD的长度
B.点B到AD的距离是BD的长度
C.点C到AD的距离是DE的长度
D.点B到AC的距离是AB的长度
10.A、B、C是直线L上三点,P为直线外一点,若PA=2cm,PB=3cm,PC=5cm,则P到直线L的距离是( )
A.等于2cm B.大于2cm C.不小于2cm D.不大于2cm
评卷人 得 分
二.填空题(共8小题)
11.在同一平面内,三条直线两两相交,最多有3个交点,那么8条直线两两相交,最多有 个交点.
12.两条直线相交,只有 个交点.
13.若a∥b,c⊥a,则c与b的位置关系是 .
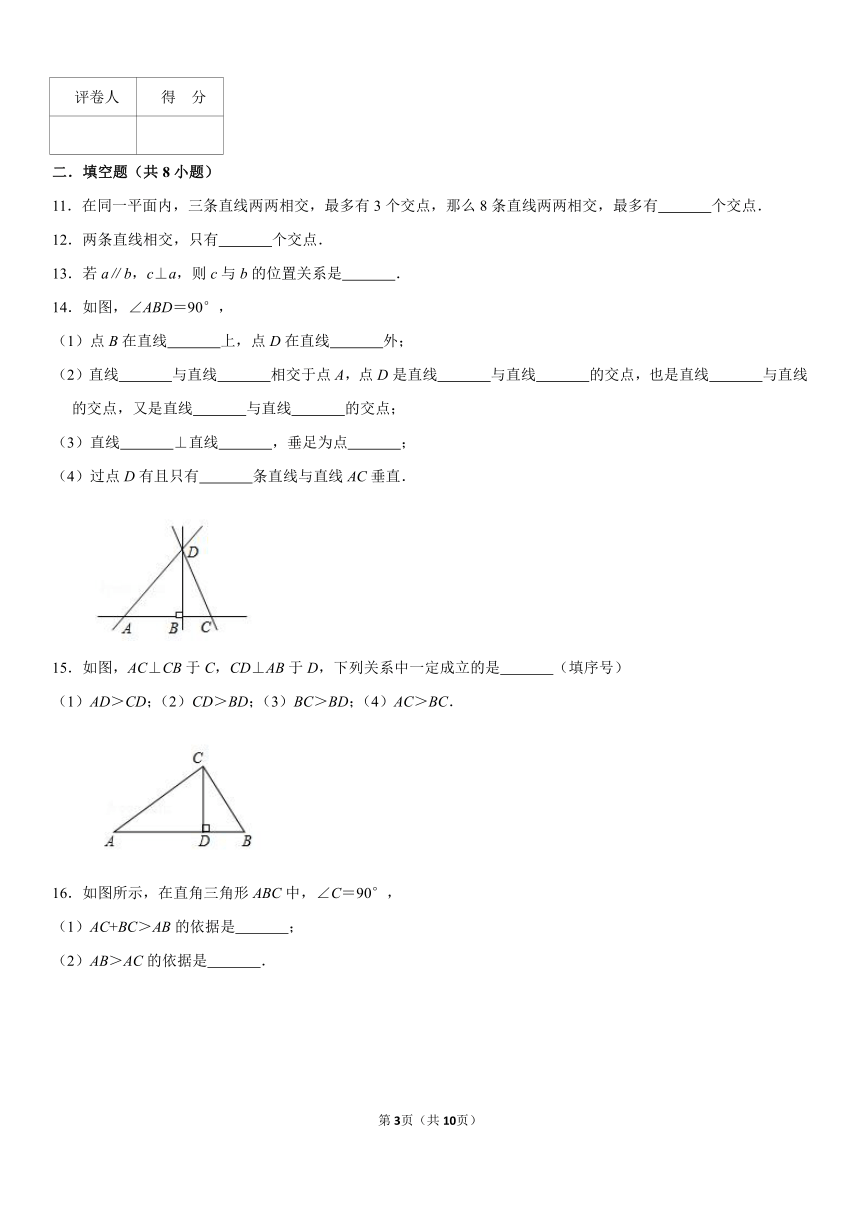
14.如图,∠ABD=90°,
(1)点B在直线 上,点D在直线 外;
(2)直线 与直线 相交于点A,点D是直线 与直线 的交点,也是直线 与直线 的交点,又是直线 与直线 的交点;
(3)直线 ⊥直线 ,垂足为点 ;
(4)过点D有且只有 条直线与直线AC垂直.
15.如图,AC⊥CB于C,CD⊥AB于D,下列关系中一定成立的是 (填序号)
(1)AD>CD;(2)CD>BD;(3)BC>BD;(4)AC>BC.
16.如图所示,在直角三角形ABC中,∠C=90°,
(1)AC+BC>AB的依据是 ;
(2)AB>AC的依据是 .
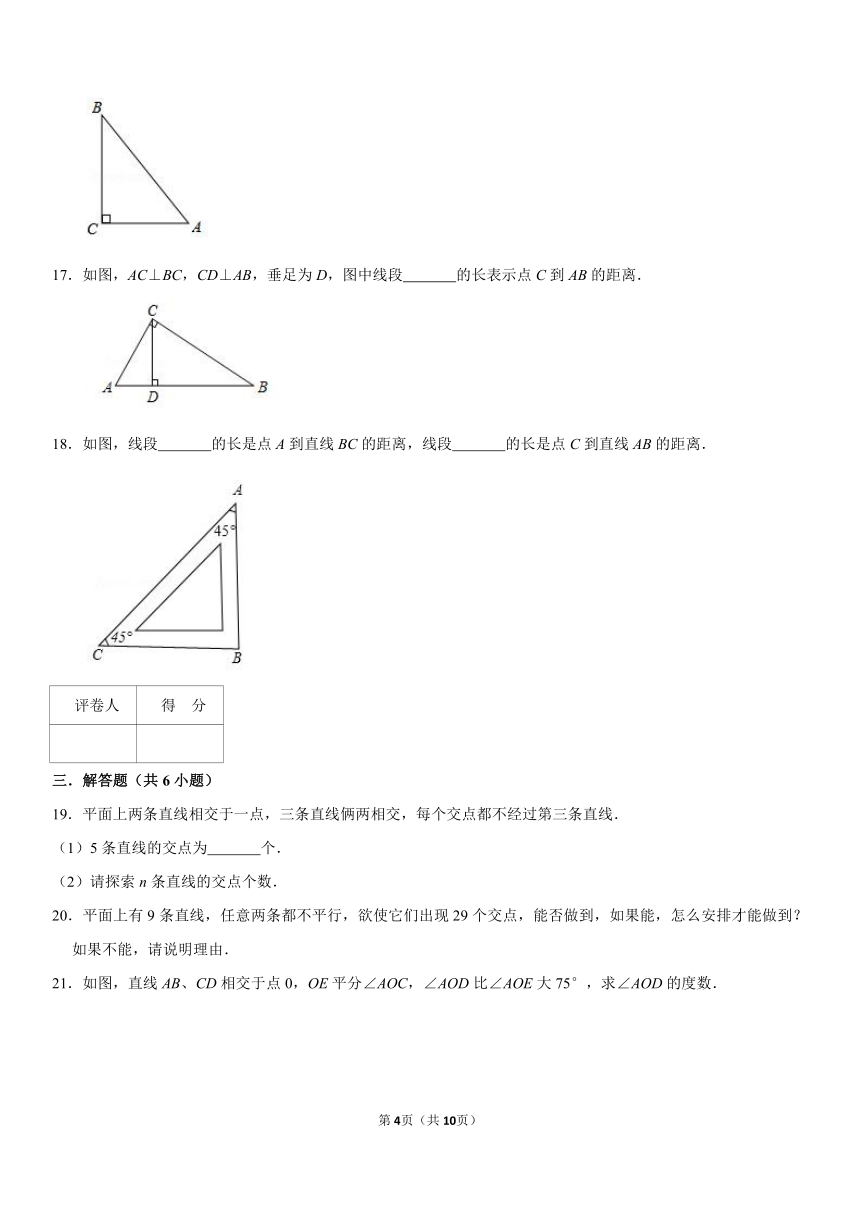
17.如图,AC⊥BC,CD⊥AB,垂足为D,图中线段 的长表示点C到AB的距离.
18.如图,线段 的长是点A到直线BC的距离,线段 的长是点C到直线AB的距离.
评卷人 得 分
三.解答题(共6小题)
19.平面上两条直线相交于一点,三条直线俩两相交,每个交点都不经过第三条直线.
(1)5条直线的交点为 个.
(2)请探索n条直线的交点个数.
20.平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.
21.如图,直线AB、CD相交于点0,OE平分∠AOC,∠AOD比∠AOE大75°,求∠AOD的度数.
22.如图,直线AB、CD交于点O,OE平分∠AOD,∠AOC=60°.试求∠BOD,∠AOD、∠EOD的度数.
23.已知:如图所示,∠1=∠2,∠3=∠4,GF⊥AB于G点,那么CD与AB是否互相垂直?试判断并说明理由.
24.你能用折纸的方法过一点作已知直线的垂线吗?
人教版2019学年初中数学7年级下《5.1 相交线》同步练习题
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:任意画三条直线,相交的情况有四种可能:
1、三直线平行,没有交点;
2、三条直线相交于同一点,一个交点;
3、两直线平行被第三直线所截,得到两个交点;
4、两直线相交得到一个交点,又被第三直线所截,共三个交点.
故选:C.
2.【解答】解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,
∵任意三条直线不过同一点,
∴此时交点为:8×(8﹣1)÷2=28,即n=28;
则m+n=29.
故选:C.
3.【解答】解:(1)互为补角的应是两个角而不是三个,故错误;
(2)没说明∠A是∠B的余角,故错误;
(3)互为邻补角的两个角的平分线互相垂直,故错误;
(4)根据对顶角的定义可判断此命题错误.
(5)相等角的余角相等,故正确.
综上可得(5)正确.
故选:A.
4.【解答】解:由图可知,∠AOC与∠BOD是对顶角,
所以,∠AOC=∠BOD.
故选:A.
5.【解答】解:①两条直线相交成四个角,如果有一对对顶角相等且均不为90°,那么这两条直线不垂直,故①错误;
②两条直线相交成四个角,则这四个角中有2对对顶角.如果三个角相等,则这四个角相等,都是直角,所以这两条直线垂直.故②正确;
③在同一平面内,过直线上一点只有一条直线与已知直线垂直.故③错误;
④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.故④错误;
综上所述,正确的说法是1个.
故选:B.
6.【解答】解:因为正方体的每一个面都是正方形,即每一个角都为90°,所以与AB垂直的边有4条.
故选:D.
7.【解答】解:∵AC⊥BC,
∴AC<AB,
∵AD⊥CD,
∴AC>CD,
∴CD<AC<AB,
∵AB=m,CD=n,
∴AC的取值范围是:大于n小于m.
故选:C.
8.【解答】解:A到直线MN的距离是3cm,根据点到直线距离的定义,3cm表示垂线段的长度,根据垂线段最短,其它线段的长度大于或等于3cm,故选D.
9.【解答】解:A、点A到BC的距离是AD的长度,本选项正确,不符合题意;
B、点B到AD的距离是BD的长度,本选项正确,不符合题意;
C、点C到AD的距离是CD的长度,故本选项错误,符合题意;
D、点B到AC的距离是AB的长度,本选项正确,不符合题意.
故选:C.
10.【解答】解:∵PA=2cm,PB=3cm,PC=5cm,
∴PA<PB<PC.
∴①当PA⊥L时,点P到直线L的距离等于2cm;
②当PA与直线L不垂直时,点P到直线L的距离小于2cm;
综上所述,则P到直线L的距离是不大于2cm.
故选:D.
二.填空题(共8小题)
11.【解答】解:交点的个数为=28,故答案为28个.
12.【解答】解:两条直线相交,只有1个交点.
13.【解答】解:根据a,b,c在空间内的位置关系可知:
1、当三条直线在同一平面内,根据两直线平行,一条直线与这两条中的一条垂直,则与另一条直线也垂直,故c与b的位置关系是:垂直;
2、当三条直线不在同一平面内,c与b的位置关系是:异面.填:垂直或异面.
14.【解答】解:(1)由图可知,点B在直线AB(或BD)上,点D在直线AC外.
(2)∵点D是直线AD,BD,CD的交点,
∴直线AD与直线AB相交于点A,点D是直线AD与直线BD的交点,也是直线AD与直线CD的交点,又是直线BD与直线CD的交点.
(3)∵∠ABD=90°,
∴直线BD⊥直线AB,垂足为点B.
(4)∵DB⊥AC,
∴过点D有且只有一条直线与直线AC垂直.
故答案为:AB(或BD),AC;AD,AB,AD,BD,AD,CD,BD,CD;BD,AB,B;一.
15.【解答】解:∵BD⊥CD,
∴BC>BD(垂线段最短).
故答案为:(3).
16.【解答】解:(1)∵∠C=90°,
∴(1)AC+BC>AB的依据是:两点之间线段最短;
(2)AB>AC的依据是:垂线段最短.
故答案为:两点之间线段最短;垂线段最短.
17.【解答】解:∵CD⊥AB,
∴线段CD的长度表示点C到AB的距离.
故答案为;CD.
18.【解答】解:点A到直线BC的垂线段是AB,所以线段AB的长是点A到直线BC的距离;
点C到直线AB的垂线段是CB,所以线段CB的长是点C到直线AB的距离.
故填AB,CB.
三.解答题(共6小题)
19.【解答】解:如图所示:
我们发现:2条直线相交有1个交点;
3条直线相交有1+2=3个交点;
4条直线相交有1+2+3=6个交点,
则5条直线的交点为1+2+3+4=10;
(2)图(n):1+2+3+…+n﹣1=.
20.【解答】解:能.理由如下:
9条直线,任意两条都不平行,最多交点的个数是==36,
∵36>29,
∴能出现29个交点,
安排如下:先使4条直线相交于一点P,另外5条直线两两相交最多可得=10个交点,
与前四条直线相交最多可得5×4=20个交点,
让其中两个点重合为点O,所以交点减少1个,
交点个数一共有10+20﹣1=29个.
故能做到.
21.【解答】解:∵AB,CD相交于点O,
∴∠AOD+∠AOC=180°,
又∵OE平分∠AOC,
∴2∠AOE=∠AOC,
∴∠AOE=(180°﹣∠AOD),
∵∠AOD﹣∠AOE=75°,
∴∠AOD﹣(180°﹣∠AOD)=75°,
∴∠AOD=165°,
∴∠AOD=110°.
22.【解答】解:∵∠AOC=60°,
∴∠BOD=∠AOC=60°,∠AOD=180°﹣∠AOC=120°.
又∵OE平分∠AOD,
∴∠EOD=∠AOD=60°.
综上所述,∠BOD、∠EOD的度数都是60°,∠AOD的度数是120°
23.【解答】解:相互垂直.
理由:∵GF⊥AB,
∴∠2+∠4=90°,
而∠1=∠2,∠3=∠4,
∴∠1+∠3=90°,
∴CD⊥AB.
24.【解答】解:先沿已知直线折一下,再在已知点处对折即可.
第10页(共10页)
