人教版2018-2019学年初中数学7年级下《5.2 平行线及其判定》同步练习题(含答案)
文档属性
| 名称 | 人教版2018-2019学年初中数学7年级下《5.2 平行线及其判定》同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 114.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-21 13:02:12 | ||
图片预览

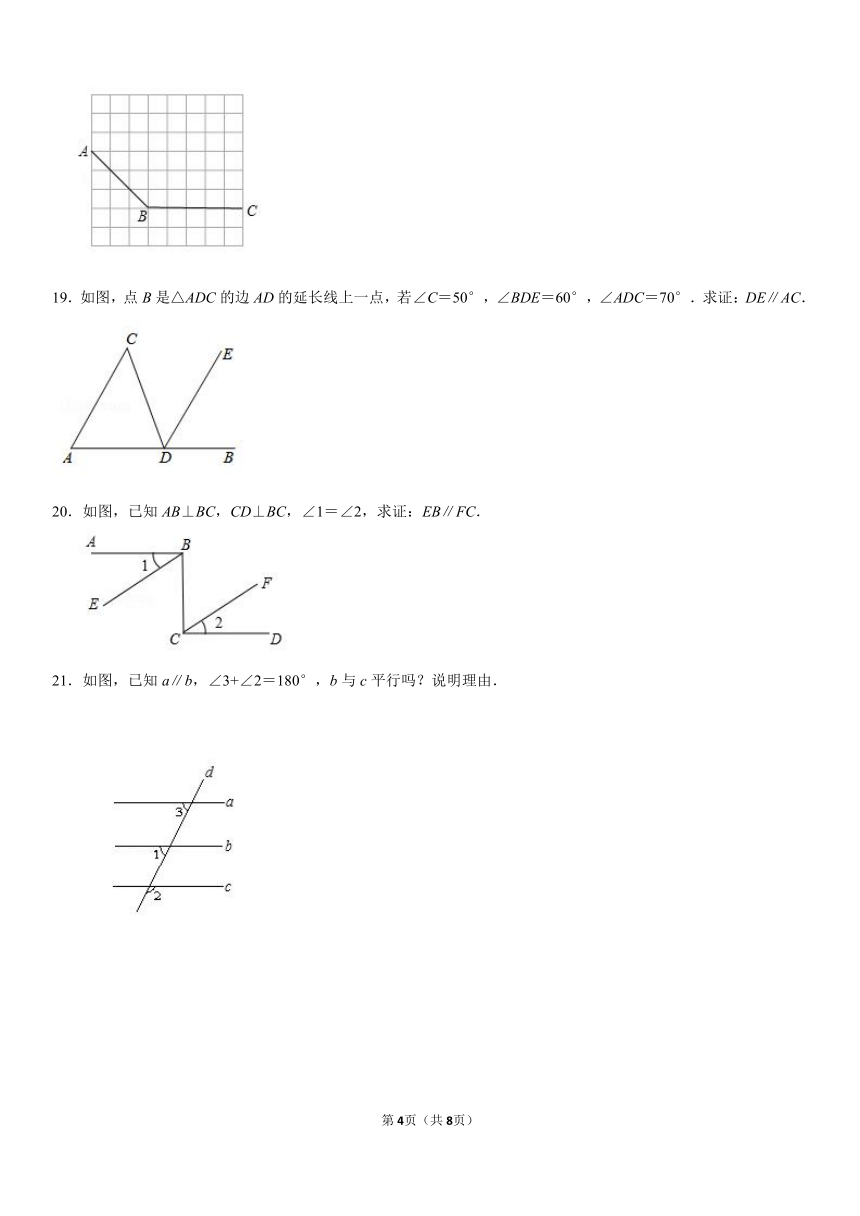
文档简介
人教版2019学年初中数学7年级下《5.2 平行线及其判定》同步练习题
评卷人 得 分
一.选择题(共8小题)
1.同一平面内,直线l与两条平行线a,b的位置关系是( )
A.l与a,b平行或相交
B.l可能与a平行,与b相交
C.l与a,b一定都相交
D.同旁内角互补,则两直线平行
2.若a⊥b,c⊥d,则a与c的关系是( )
A.平行 B.垂直 C.相交 D.以上都不对
3.下面说法正确的是( )
A.过两点有且只有一条直线
B.平角是一条直线
C.两条直线不相交就一定平行
D.过一点有且只有一条直线与已知直线平行
4.在同一平面内有三条直线,若其中有两条且只有两条直线平行,则这三条直线交点的个数为( )
A.0个 B.1个 C.2个 D.3个
5.下列说法中正确的是( )
A.过点P画线段AB的垂线
B.P是直线外一点,Q是直线上一点,连接PQ,PQ⊥AB
C.过一点有且只有一条直线平行于已知直线
D.线段AB就是表示A,B两点间的距离
6.过直线l外一点A作l的平行线,可以作( )条.
A.1 B.2 C.3 D.4
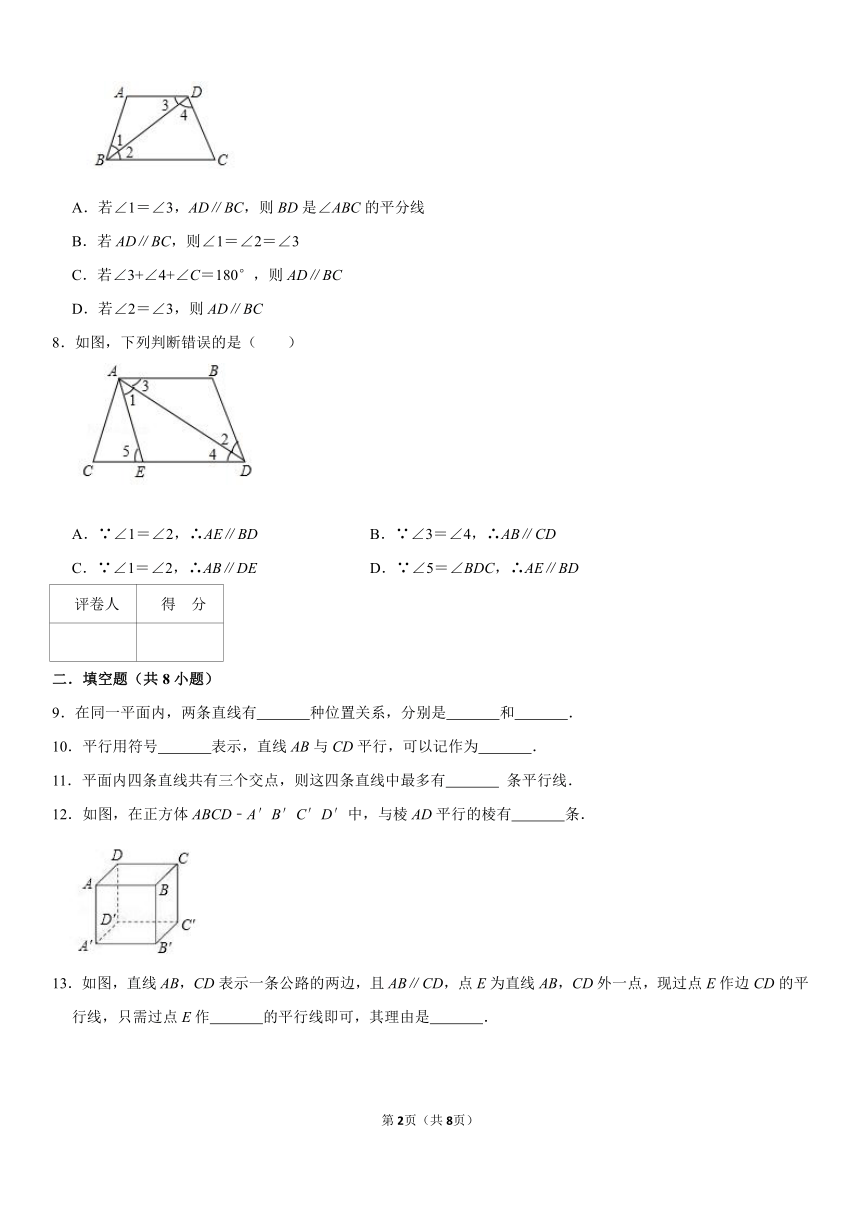
7.如图所示,下列判断错误的是( )
A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线
B.若AD∥BC,则∠1=∠2=∠3
C.若∠3+∠4+∠C=180°,则AD∥BC
D.若∠2=∠3,则AD∥BC
8.如图,下列判断错误的是( )
A.∵∠1=∠2,∴AE∥BD B.∵∠3=∠4,∴AB∥CD
C.∵∠1=∠2,∴AB∥DE D.∵∠5=∠BDC,∴AE∥BD
评卷人 得 分
二.填空题(共8小题)
9.在同一平面内,两条直线有 种位置关系,分别是 和 .
10.平行用符号 表示,直线AB与CD平行,可以记作为 .
11.平面内四条直线共有三个交点,则这四条直线中最多有 条平行线.
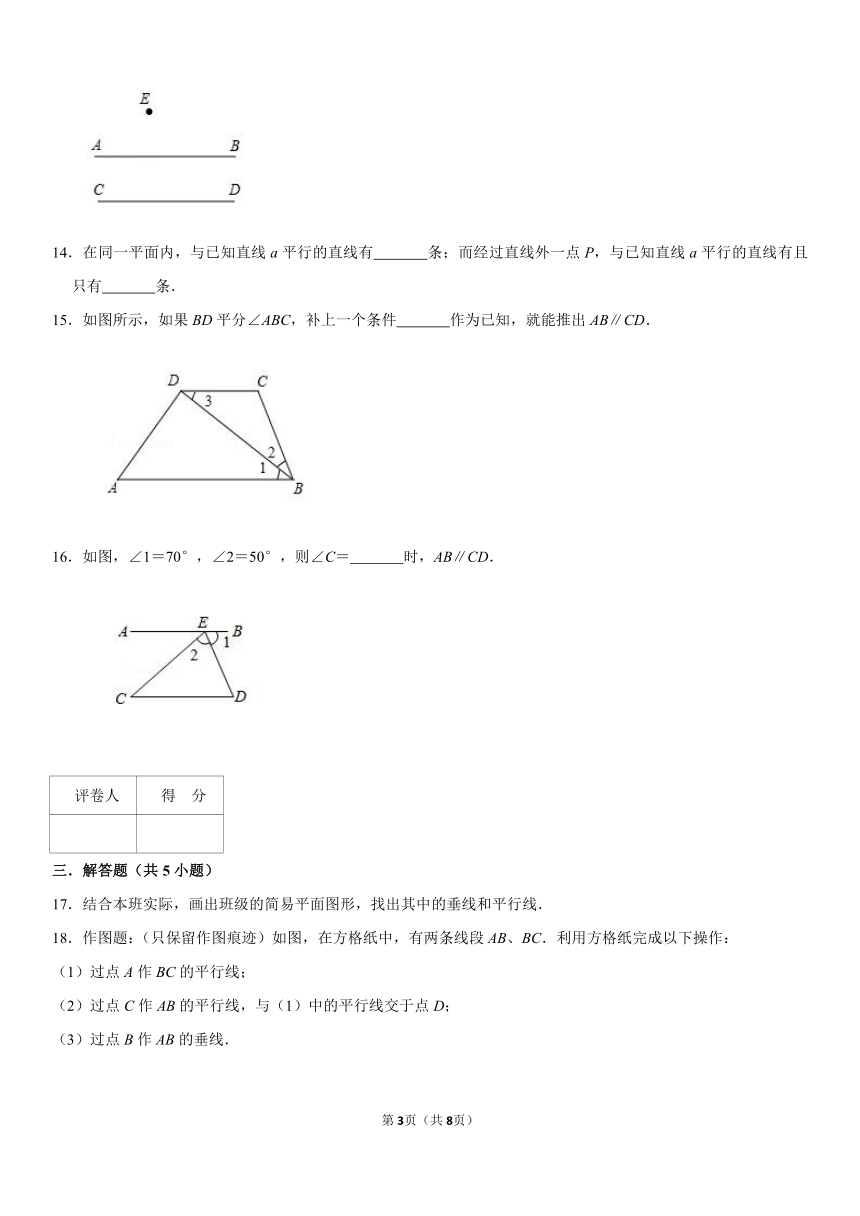
12.如图,在正方体ABCD﹣A′B′C′D′中,与棱AD平行的棱有 条.
13.如图,直线AB,CD表示一条公路的两边,且AB∥CD,点E为直线AB,CD外一点,现过点E作边CD的平行线,只需过点E作 的平行线即可,其理由是 .
14.在同一平面内,与已知直线a平行的直线有 条;而经过直线外一点P,与已知直线a平行的直线有且只有 条.
15.如图所示,如果BD平分∠ABC,补上一个条件 作为已知,就能推出AB∥CD.
16.如图,∠1=70°,∠2=50°,则∠C= 时,AB∥CD.
评卷人 得 分
三.解答题(共5小题)
17.结合本班实际,画出班级的简易平面图形,找出其中的垂线和平行线.
18.作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段AB、BC.利用方格纸完成以下操作:
(1)过点A作BC的平行线;
(2)过点C作AB的平行线,与(1)中的平行线交于点D;
(3)过点B作AB的垂线.
19.如图,点B是△ADC的边AD的延长线上一点,若∠C=50°,∠BDE=60°,∠ADC=70°.求证:DE∥AC.
20.如图,已知AB⊥BC,CD⊥BC,∠1=∠2,求证:EB∥FC.
21.如图,已知a∥b,∠3+∠2=180°,b与c平行吗?说明理由.
人教版2019学年初中数学7年级下《5.2 平行线及其判定》
同步练习题
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:A、由于同一平面内两直线的位置关系只有两种:平行和相交,当l与a平行,根据平行公理的推论可知l也与b平行;当l与a相交,则必然与b相交,此选项正确;
B、根据A的分析可知l不可能与a平行,而与b相交,此选项错误;
C、根据A的分析,l也可能与a、b都平行,此选项错误;
D、若三条直线都平行,也就不存在同旁内角了,此选项错误.
故选:A.
2.【解答】解:当b∥d时a∥c;
当b和d相交但不垂直时,a与c相交;
当b和d垂直时,a与c垂直;
a和c可能平行,也可能相交,还可能垂直,
故选:D.
3.【解答】解:A、由直线公理可知,过两点有且只有一条直线,故本选项正确;
B、平角是有公共端点是两条射线组成的图形,故本选项错误;
C、同一平面内两条直线不相交就一定平行,故本选项错误;
D、经过直线外一点有且只有一条直线与已知直线平行,故本选项错误.
故选:A.
4.【解答】解:根据题意,第三条直线与这两条平行直线各有一个交点.
故选:C.
5.【解答】解:A、正确;
B、这种作法不一定垂直,错误;
C、必须强调过直线外一点,错误;
D、必须强调线段AB的长度,错误.
故选:A.
6.【解答】解:因为平行公理:过已知直线外一点有且只有一条直线与已知直线平行.故选A.
7.【解答】解:A、∵AD∥BC,
∴∠2=∠3,
又∵∠1=∠3,
∴∠1=∠2,则BD是∠ABC的平分线;
B、∠2,∠3是直线AD和直线BC被直线BD所截形成的内错角,若AD∥BC,则∠2=∠3,∠1是直线AB和直线AD被直线BD所截形成的角,因此,若AD∥BC,不能证明∠1=∠2=∠3;
C、∠3+∠4+∠C=180°,即同旁内角∠ADC+∠C=180°,则AD∥BC;
D、内错角∠2=∠3,则AD∥BC.
故选:B.
8.【解答】解:A、∵∠1=∠2,
∴AE∥BD(内错角相等,两直线平行),故此选项不合题意;
B、∵∠3=∠4,
∴AB∥CD(内错角相等,两直线平行),故此选项不合题意;
C、∵∠1=∠2,
∴AB∥DE错误,应该是AE∥BD,故此选项符合题意;
D、∵∠5=∠BDC,
∴AE∥BD(同位角相等,两直线平行),故此选项不合题意;
故选:C.
二.填空题(共8小题)
9.【解答】解:在同一平面内,两条直线有两种位置关系,分别是平行和相交.
故答案为:两;平行;相交.
10.【解答】解:平行用符号∥表示,如果直线AB与CD平行,可以记作为:AB∥CD.
故答案为:∥,AB∥CD.
11.【解答】解:若四条直线相互平行,则没有交点;
若四条直线中有三条直线相互平行,则此时恰好有三个交点;
若四条直线中有两条直线相互平行,另两条不平行,则此时有三个交点或五个交点;
若四条直线中有两条直线相互平行,另两条也平行,但它们之间相互不平行,则此时有四个交点;
若四条直线中没有平行线,则此时的交点是一个或四个或六个.
综上可知,平面内四条直线共有三个交点,则这四条直线中最多有三条平行线.
故答案是:三.
12.【解答】解:与棱AD平行的棱有:BC,B′C′,A′D′,共有三条.
13.【解答】解:只需过点E作AB的平行线即可,其理由是平行于同一直线的两直线互相平行.
故答案为:AB,平行于同一直线的两直线互相平行.
14.【解答】解:在同一平面内,与已知直线a平行的直线有无数条;
而经过直线外一点P,与已知直线a平行的直线有且只有1条.
15.【解答】解:可添加∠2=∠3;
∵BD平分∠ABC,∴∠1=∠2,
若∠2=∠3,∴可得∠1=∠3,
∴AB∥CD.
16.【解答】解:∵∠1=70°,∠2=50°,
∴∠AEC=180°﹣70°﹣50°=60°,
当∠C=∠AEC=60°时,AB∥CD.
故答案为:60°
三.解答题(共5小题)
17.【解答】解:如图所示:
垂线:AB⊥BC,AB⊥AD,CD⊥BC,CD⊥AD;
平行线:AB∥CD,AD∥BC.
18.【解答】解:
(1)A所在的横线就是满足条件的直线,即AE就是所求;
(2)在直线AE上,到A距离是5个格长的点就是D,则CD就是所求与AB平行的直线;
(3)AE上D右边的个点F,过B,F作直线,就是所求.
19.【解答】证明:∵∠BDE=60°,∠ADC=70°.
∴∠CDE=180°﹣60°﹣70°=50°,
∵∠C=50°,
∴∠C=∠CDE,
∴AC∥DE.
20.【解答】证明:∵AB⊥BC,CD⊥BC(已知),
∴∠ABC=∠BCD=90°(垂直定义);
又∵∠1=∠2(已知),
∴∠ABC﹣∠1=∠BCD﹣∠2(等量减等量,差相等),
∴∠EBC=∠FCB,
∴EB∥FC(内错角相等,两直线平行).
21.【解答】解:b与c平行.
证明:∵∠2=∠4,∠3+∠2=180°,
∴∠3+∠4=180°;
∴a∥c(同旁内角互补,两直线平行);
∴b∥c.
第8页(共8页)
