人教版2018-2019学年初中数学7年级下《5.3 平行线的性质》同步练习题(含答案)
文档属性
| 名称 | 人教版2018-2019学年初中数学7年级下《5.3 平行线的性质》同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-21 13:04:22 | ||
图片预览


文档简介
人教版初中数学7年级下《5.3 平行线的性质》同步练习题
评卷人 得 分
一.选择题(共10小题)
1.如图,BC⊥AE,垂足为C,过C作CD∥AB,若∠ECD=43°,则∠B=( )
A.43° B.57° C.47° D.45°
2.如图,直线EF分别交AB、CD于点E、F,EG平分∠BEF,AB∥CD.若∠1=72°,则∠2的度数为( )
A.54° B.59° C.72° D.108°
3.如图所示,AB⊥EF,CD⊥EF,∠1=∠F=40°,且A,C,F三点共线,那么与∠FCD相等的角有( )
A.1个 B.2个 C.3个 D.4个
4.如图,已知∠1=∠2,则能得到正确的结论是( )
A.AC⊥AB B.AB=CD C.AD∥BC D.AB∥CD
5.如图,AB∥DC,ED∥BC,AE∥BD,那么图中和△ABD面积相等的三角形(不包括△ABD)有( )
A.1个 B.2个 C.3个 D.4个
6.如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,若S△ABD=10cm2,S△ACD为( )
A.10 B.9 C.8 D.7
7.下列命题中的假命题是( )
A.一组邻边相等的平行四边形是菱形
B.一组对边平行且相等的四边形是平行四边形
C.一组邻边相等的矩形是正方形
D.一组对边相等且有一个角是直角的四边形是矩形
8.“两点确定一条直线”这句话是( )
A.定理 B.基本事实 C.结论 D.定义
9.一座大楼有4部电梯,每部电梯可停靠六层(不一定是连续六层,也不一定停最底层).对大楼中任意的两层,至少有一部电梯可同时停靠,则这座大楼最多有( )层.
A.11 B.12 C.13 D.14
10.在期中考试中,同学甲、乙、丙、丁分别获得第一、第二、第三、第四名.在期末考试中,他们又是班上的前四名.如果他们当中只有一位的排名与期中考试中的排名相同,那么排名情况有( )种可能.
A.5 B.6 C.7 D.8
评卷人 得 分
二.填空题(共9小题)
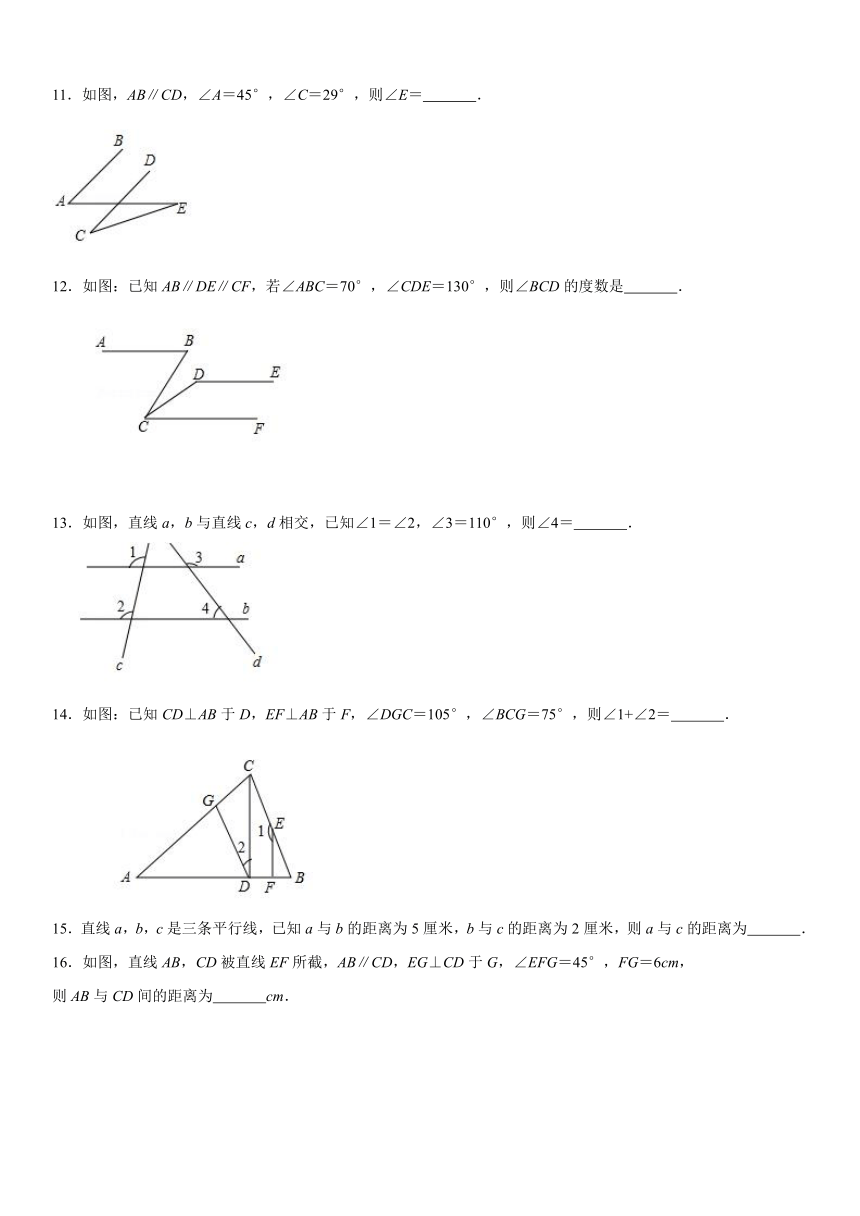
11.如图,AB∥CD,∠A=45°,∠C=29°,则∠E= .
12.如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,则∠BCD的度数是 .
13.如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4= .
14.如图:已知CD⊥AB于D,EF⊥AB于F,∠DGC=105°,∠BCG=75°,则∠1+∠2= .
15.直线a,b,c是三条平行线,已知a与b的距离为5厘米,b与c的距离为2厘米,则a与c的距离为 .
16.如图,直线AB,CD被直线EF所截,AB∥CD,EG⊥CD于G,∠EFG=45°,FG=6cm,
则AB与CD间的距离为 cm.
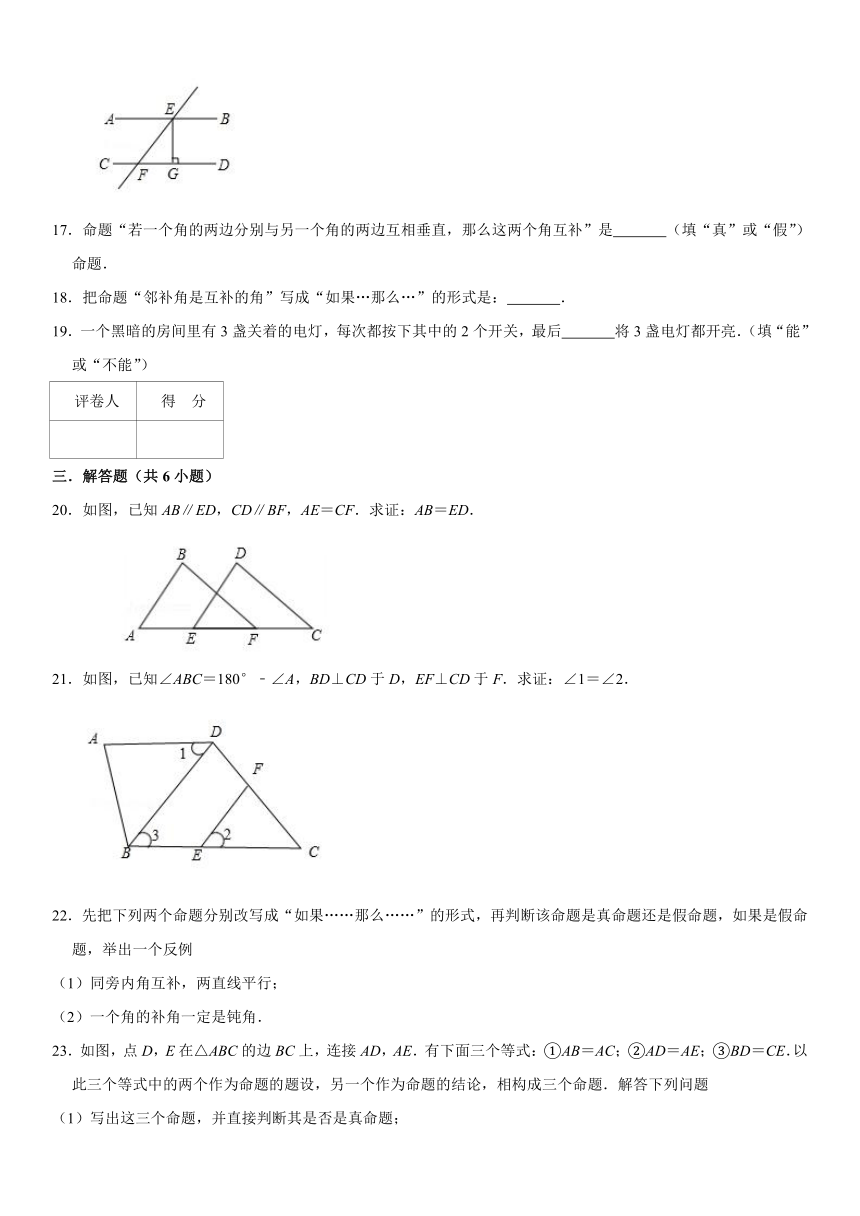
17.命题“若一个角的两边分别与另一个角的两边互相垂直,那么这两个角互补”是 (填“真”或“假”)命题.
18.把命题“邻补角是互补的角”写成“如果…那么…”的形式是: .
19.一个黑暗的房间里有3盏关着的电灯,每次都按下其中的2个开关,最后 将3盏电灯都开亮.(填“能”或“不能”)
评卷人 得 分
三.解答题(共6小题)
20.如图,已知AB∥ED,CD∥BF,AE=CF.求证:AB=ED.
21.如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于F.求证:∠1=∠2.
22.先把下列两个命题分别改写成“如果……那么……”的形式,再判断该命题是真命题还是假命题,如果是假命题,举出一个反例
(1)同旁内角互补,两直线平行;
(2)一个角的补角一定是钝角.
23.如图,点D,E在△ABC的边BC上,连接AD,AE.有下面三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成三个命题.解答下列问题
(1)写出这三个命题,并直接判断其是否是真命题;
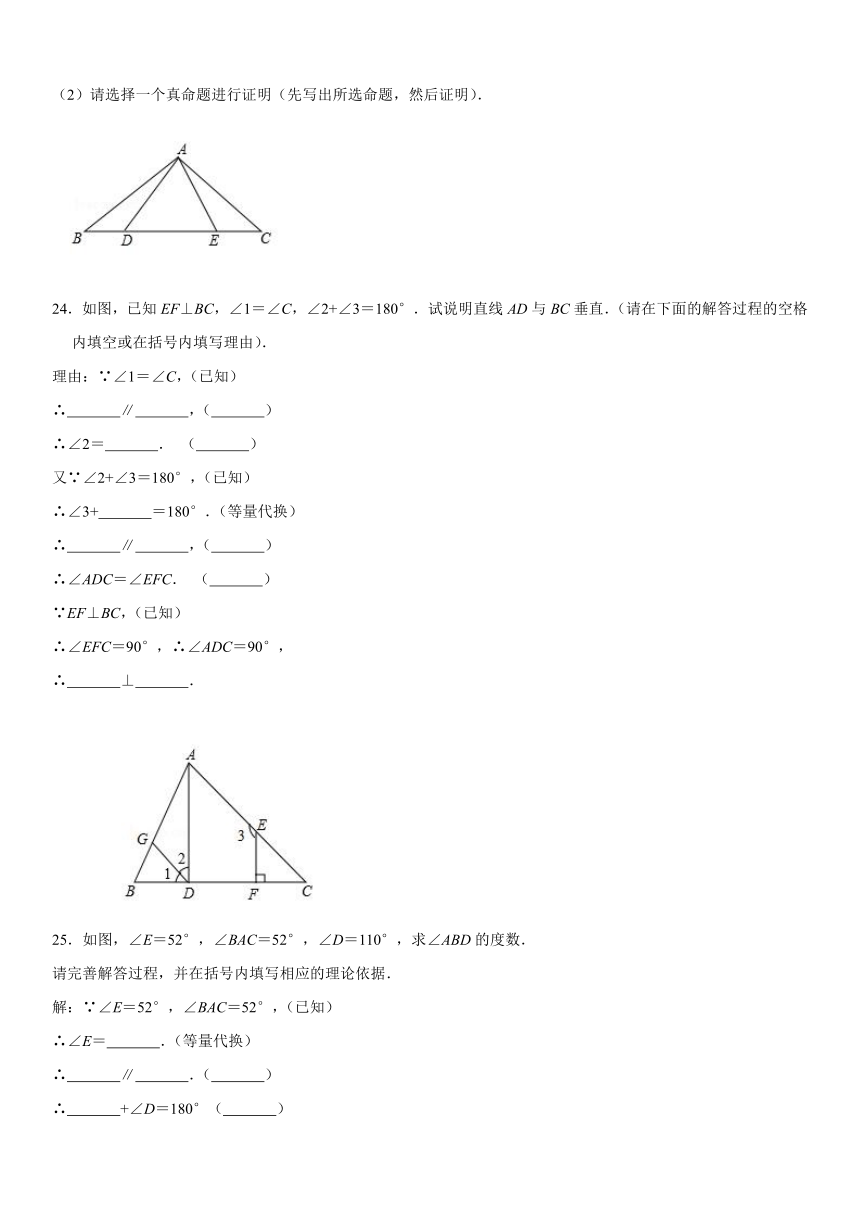
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
24.如图,已知EF⊥BC,∠1=∠C,∠2+∠3=180°.试说明直线AD与BC垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).
理由:∵∠1=∠C,(已知)
∴ ∥ ,( )
∴∠2= . ( )
又∵∠2+∠3=180°,(已知)
∴∠3+ =180°.(等量代换)
∴ ∥ ,( )
∴∠ADC=∠EFC. ( )
∵EF⊥BC,(已知)
∴∠EFC=90°,∴∠ADC=90°,
∴ ⊥ .
25.如图,∠E=52°,∠BAC=52°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=52°,∠BAC=52°,(已知)
∴∠E= .(等量代换)
∴ ∥ .( )
∴ +∠D=180°( )
∵∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
人教版初中数学7年级下《5.3 平行线的性质》同步练习题
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:∵BC⊥AE,
∴∠ACB=90°,
∵CD∥AB,
∴∠ECD=∠A=43°,
∴∠B=90°﹣∠A=47°,
故选:C.
2.【解答】解:∵AB∥CD,
∴∠BEF=180°﹣∠1=180°﹣72°=108°,∠2=∠BEG,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=×108°=54°,
∴∠2=∠BEG=54°.
故选:A.
3.【解答】解:∵AB⊥EF,CD⊥EF,
∴AB∥CD,
∴∠FCD=∠A,
∵∠1=∠F=40°,
∴BG∥AF,
∴∠A=∠ABG;
∴与∠FCD相等的角有∠A,∠ABG,
故选:B.
4.【解答】解:∵∠1=∠2,且它们是由AB,CD被AC所截而成的内错角,
∴AB∥CD,
故选:D.
5.【解答】解:∵AB∥DC,
∴△ABC与△ABD的面积相等,
∵AE∥BD,
∴△BED与△ABD的面积相等,
∵ED∥BC找不到与△ABD等底等高的三角形,
∴和△ABD的面积相等的三角形有△ABC、△BDE,共2个.
故选:B.
6.【解答】解∵四边形ABCD中,AD∥BC,AC与BD相交于点O,S△ABD=10cm2,
∴△ABD和△ACD如果都以AD做底边时,此时底边上的高相等,
∴S△ACD=10cm2,
故选:A.
7.【解答】解:A、一组邻边相等的平行四边形是菱形,正确;
B、一组对边平行且相等的四边形是平行四边形,正确;
C、一组邻边相等的矩形是正方形,正确;
D、一组对边平行且相等且有一个角是直角的四边形是矩形,故错误.
故选:D.
8.【解答】解:“两点确定一条直线”这句话是基本事实;
故选:B.
9.【解答】解:首先把楼层看作点,
大楼中任意的两层,有一部电梯都可停靠,则两层所代表的点之间可以连一条线段,
每部电梯可停靠六层,则这六层所代表的点之间可以连:5+4+3+2+1=15条线段,
则四部电梯最多可以连15×4=60条线段,
∵7层楼需要:6+5+4+3+2+1=21条线段,
8层楼需要:7+6+5+4+3+2+1=28条线段,
9层楼需要:8+7+6+5+4+3+2+1=36条线段,
10层楼需要:9+8+7+6+5+4+3+2+1=45条线段,
11层楼需要:10+9+8+7+6+5+4+3+2+1=55条线段,
12层楼需要:11+10+9+8+7+6+5+4+3+2+1=66条线段,
∴这个大楼的层数不超过11层.
故选:A.
10.【解答】解:他们当中只有一位的排名与期中考试中的排名相同有4种可能,第二位同学的排名有2种可能,第三位与第四位的排名是确定的.
(如:甲的排名没有变,仍为第一,则乙到了第三或第四.假设乙到了第四,则丙就是第二,丁第三.)
所以有2×4=8种.
故选:D.
二.填空题(共9小题)
11.【解答】解:如图,∵AB∥CD,∠A=45°,
∴∠DOE=∠A=45°,
∵∠C=29°,
∴∠E=∠DOE﹣∠C=45°﹣29°=16°,
故答案为:16°.
12.【解答】解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°,
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°,
∴∠DCF=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.
故答案为:20°.
13.【解答】解:∵∠3=∠5=110°,
∵∠1=∠2=58°,
∴a∥b,
∴∠4+∠5=180°,
∴∠4=70°,
故答案为:70°
14.【解答】解:∵CD⊥AB,EF⊥AB,
∴DC∥EF,
∴∠DCB=∠BEF,
∵∠DGC=105°,∠BCG=75°,
∴∠DGC+∠BCG=180°,
∴BC∥GD,
∴∠2=∠DCB,
∴∠2=∠BEF,
∵∠1+∠BEF=180°,
∴∠1+∠2=180°.
故答案为:180°.
15.【解答】解:应分两种情况:
①如图:
a与c的距离为:5+2=7(厘米);
②如图:
a与c的距离为:5﹣2=3(厘米).
综上所述,a与c的距离为7厘米或3厘米.
故答案为:7厘米或3厘米.
16.【解答】解:∵EG⊥CD,
∴∠EGF=90°,
∵∠EFG=45°,
∴∠FEG=45°,
∴FG=EG,
∵FG=6cm,
∴EG=6cm,
∴AB与CD间的距离为6cm.
故答案为:6.
17.【解答】解:如图1,∠O和∠C的两边互相垂直,∠O和∠C互补,
如图2,∠1和∠2的两边互相垂直,∠1=∠2,
∴若一个角的两边分别与另一个角的两边互相垂直,那么这两个角相等或互补,
∴若一个角的两边分别与另一个角的两边互相垂直,那么这两个角互补是假命题,
故答案为:假.
18.【解答】解:把命题“邻补角是互补的角”改写为“如果…那么…”的形式是:如果两个角是邻补角,那么它们(这两个角)互补.
故答案为:如果两个角是邻补角,那么它们(这两个角)互补.
19.【解答】解:∵一个黑暗的房间里有3盏关着的电灯,每次都按下其中的2个开关,
∴第一次按下后有两盏电灯亮着,有一盏电灯不亮,
这样再继续按两个开关,不论怎样一定会至少有一盏电灯不亮,故最后不能将3盏电灯都开亮.
故答案为:不能.
三.解答题(共6小题)
20.【解答】证明:∵AB∥ED,CD∥BF,
∴∠A=∠DEC,∠C=∠AFB,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在△ABF与△EDC中,
∴△ABF≌△EDC,(ASA),
∴AB=ED.
21.【解答】证明:∵∠ABC=180°﹣∠A,
∴∠ABC+∠A=180°,
∴AD∥BC,
∴∠3=∠1,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠2=∠3,
∴∠1=∠2.
22.【解答】解:(1)如果两条直线被第三条直线所截得的同旁内角互补,那么这两条直线平行.
是真命题.
(2)如果一个角是另一个角的补角,那么这个角一定是钝角.
是假命题;
如:设∠1=60°,∠2=120°,∠1是∠2的补角,但∠1不是钝角.
23.【解答】解:(1)三个命题如下:命题Ⅰ“如果①②成立,那么③成立”;
命题Ⅱ“如果①③成立,那么②成立”;
命题Ⅲ“如果②③成立,那么①成立,这三个命题都是真命题.
(2)选择命题Ⅱ“如果①③成立,那么②成立”:
证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
∵
∴△ABD≌△ACE(SAS),
∴AD=AE.
24.【解答】解:∵∠1=∠C,(已知)
∴GD∥AC,(同位角相等,两直线平行)
∴∠2=∠DAC.(两直线平行,内错角相等)
又∵∠2+∠3=180°,(已知)
∴∠3+∠DAC=180°.(等量代换)
∴AD∥EF,(同旁内角互补,两直线平行)
∴∠ADC=∠EFC.(两直线平行,同位角相等)
∵EF⊥BC,(已知 )
∴∠EFC=90°,
∴∠ADC=90°,
∴AD⊥BC.
故答案为:GD,AC,同位角相等,两直线平行;∠DAC,两直线平行,内错角相等;∠DAC;AD,EF,同旁内角互补,两直线平行;两直线平行,同位角相等;AD,BC.
25.【解答】解:∵∠E=52°,∠BAC=52°(已知)
∴∠E=∠BAC(等量代换)
∴AB∥ED(同位角相等,两直线平行)
∴∠ABD+∠D=180°(两直线平行,同旁内角互补)
∵∠D=110°(已知)
∴∠ABD=70°(等式的性质)
故答案为:∠BAC;AB,ED; 同位角相等,两直线平行;∠ABD;两直线平行,同旁内角互补.
