人教版2018-2019学年初中数学7年级下《5.4 平移》同步练习题(含答案)
文档属性
| 名称 | 人教版2018-2019学年初中数学7年级下《5.4 平移》同步练习题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 218.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-21 13:06:01 | ||
图片预览

文档简介
人教版2019学年初中数学7年级下《5.4 平移》同步练习题
评卷人 得 分
一.选择题(共10小题)
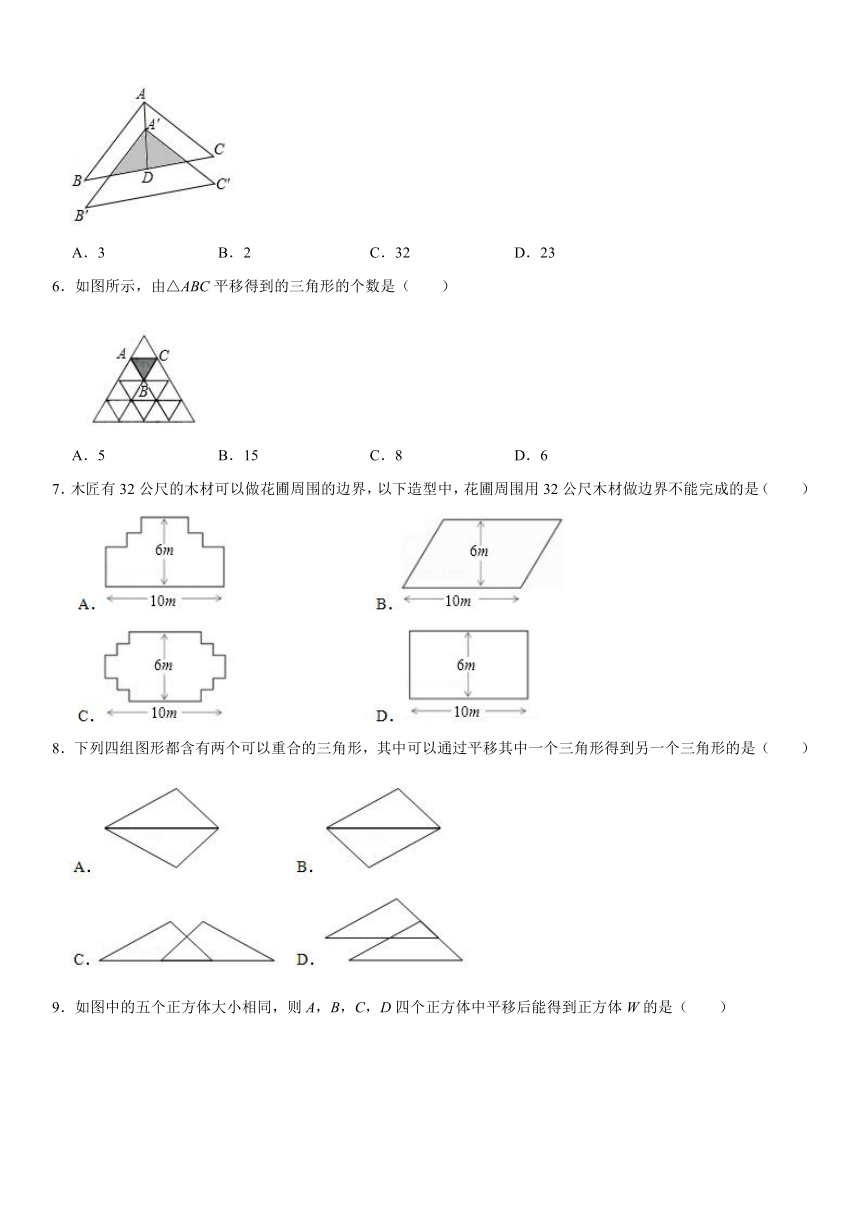
1.下列生活现象中,属于平移的是( )
A.足球在草地上滚动 B.拉开抽屉
C.把打开的课本合上 D.钟摆的摆动
2.下列各现象中:①电梯的升降,②照镜子,③钟表分针的运动,④行驶中汽车车轮的运动,其中是平移现象的个数有( )
A.1个 B.2个 C.3个 D.4个
3.下列图形中,哪个可以通过如图平移得到( )
4.某酒店打算在一段楼梯面上铺上宽为2米的地毯,台阶的侧面如图所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要( )
A.2560元 B.2620元 C.2720元 D.2840元
5.如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为18,阴影部分三角形的面积为8.若AA'=1,则A'D等于( )
A.3 B.2 C.32 D.23
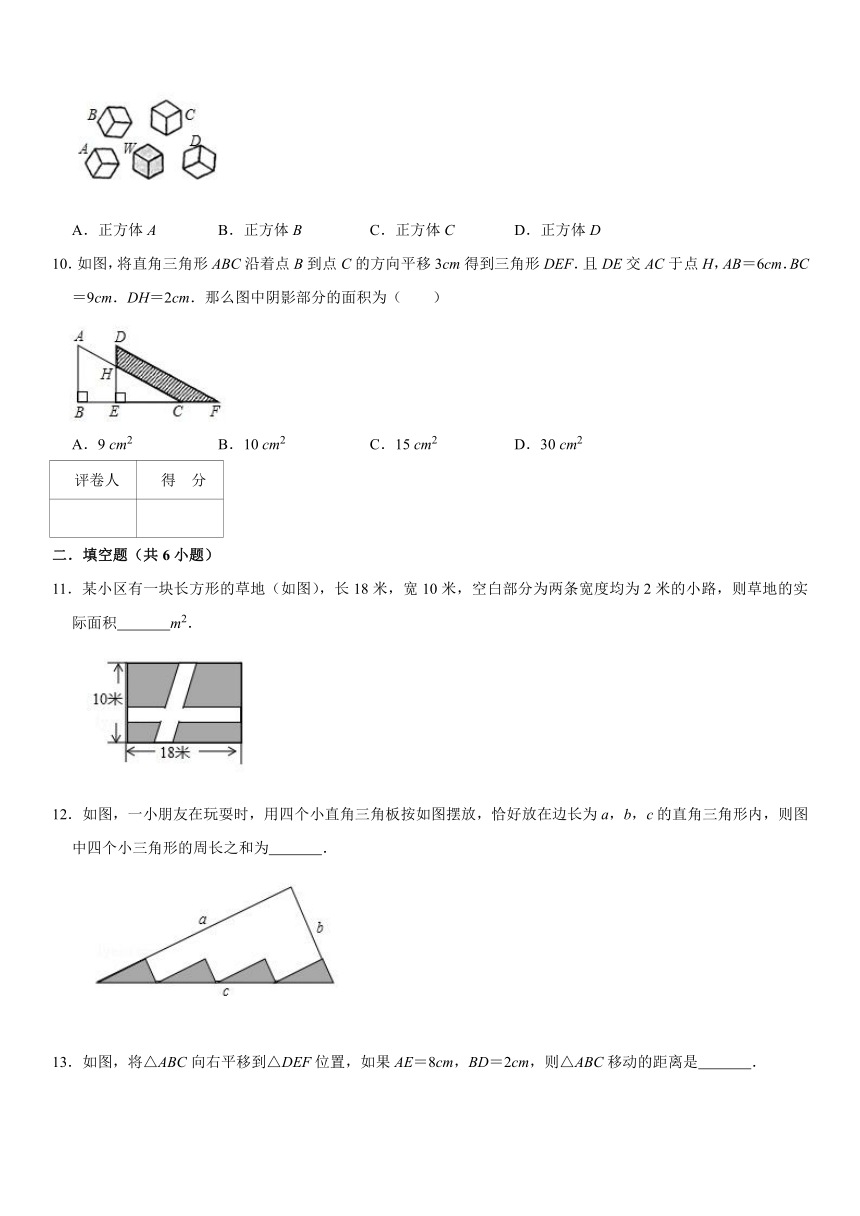
6.如图所示,由△ABC平移得到的三角形的个数是( )
A.5 B.15 C.8 D.6
7.木匠有32公尺的木材可以做花圃周围的边界,以下造型中,花圃周围用32公尺木材做边界不能完成的是( )
8.下列四组图形都含有两个可以重合的三角形,其中可以通过平移其中一个三角形得到另一个三角形的是( )
9.如图中的五个正方体大小相同,则A,B,C,D四个正方体中平移后能得到正方体W的是( )
A.正方体A B.正方体B C.正方体C D.正方体D
10.如图,将直角三角形ABC沿着点B到点C的方向平移3cm得到三角形DEF.且DE交AC于点H,AB=6cm.BC=9cm.DH=2cm.那么图中阴影部分的面积为( )
A.9 cm2 B.10 cm2 C.15 cm2 D.30 cm2
评卷人 得 分
二.填空题(共6小题)
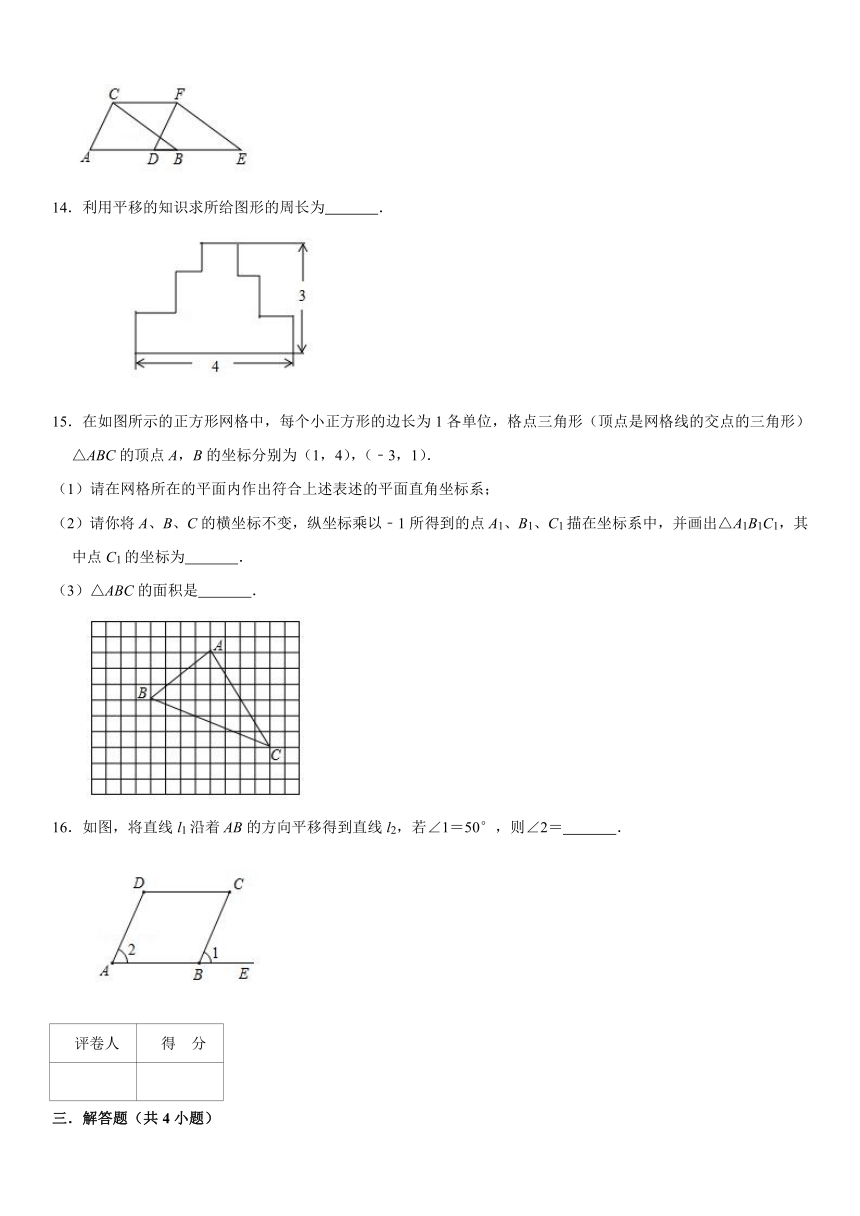
11.某小区有一块长方形的草地(如图),长18米,宽10米,空白部分为两条宽度均为2米的小路,则草地的实际面积 m2.
12.如图,一小朋友在玩耍时,用四个小直角三角板按如图摆放,恰好放在边长为a,b,c的直角三角形内,则图中四个小三角形的周长之和为 .
13.如图,将△ABC向右平移到△DEF位置,如果AE=8cm,BD=2cm,则△ABC移动的距离是 .
14.利用平移的知识求所给图形的周长为 .
15.在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 .
(3)△ABC的面积是 .
16.如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2= .
评卷人 得 分
三.解答题(共4小题)
17.如图所示,多边形ABCDEFGH是一块从一边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,求这块垫片的周长.
18.如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,问这块红地毯至少要多大?
19.如图,两个直角三角形重叠在一起,将其中一个三角形沿着BC边平移到△DEF的位置,∠B=90°,AB=10,DH=3,平移距离为6,求阴影部分的面积(单位:厘米)
20.如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).三角形AOB中任意一点P(x0,y0)经平移后的对应点为P1(x0+2,y0),并且点A,O,B的对应点分别为点D,E,F.
(1)指出平移的方向和距离;
(2)画出平移后的三角形DEF并标出D、E、F点的坐标;
(3)求线段OA在平移过程中扫过的面积.
人教版2019学年初中数学7年级下《5.4 平移》同步练习题
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:A.足球在草地上滚动方向变化,不符合平移的定义,不属于平移,故本选项错误;
B.拉开抽屉符合平移的定义,属于平移,故本选项正确;
C.把打开的课本合上,不符合平移的定义,不属于平移,故本选项错误;
D.钟摆的摆动是旋转运动,不属于平移,故本选项错误;
故选:B.
2.【解答】解:①电梯的升降,是平移;
②照镜子,是轴对称;
③钟表分针的运动,是旋转;
④行驶中汽车车轮的运动,是旋转;
故是平移现象的个数有1个.
故选:A.
3.【解答】解:A、没有改变图形的形状,对应线段平行且相等,符合题意,故此选项正确;
B、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误;
C、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误;
D、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误.
故选:A.
4.【解答】解:如图,利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为=12米、5米,
∴地毯的长度为12+5=17米,地毯的面积为17×2=34平方米,
∴购买这种地毯至少需要80×34=2720元.
故选:C.
5.【解答】解:如图,
∵S△ABC=18、S△A′EF=8,且AD为BC边的中线,
∴S△A′DE=S△A′EF=4,S△ABD=S△ABC=9,
∵将△ABC沿BC边上的中线AD平移得到△A'B'C',
∴A′E∥AB,
∴△DA′E∽△DAB,
则()2=,即()2=,
解得A′D=2(负值舍去),
故选:B.
6.【解答】解:平移变换不改变图形的形状、大小和方向,
因此由△ABC平移得到的三角形有5个.
故选:A.
7.【解答】解:A、周长=2(10+6)=32m;
B、∵垂线段最短,
∴平行四边形的另一边一定大于6m,
∵2(10+6)=32m,
∴周长一定大于32m;
C、周长=2(10+6)=32m;
D、周长=2(10+6)=32m;
故选:B.
8.【解答】解:A、可以通过轴对称得到,故此选项错误;
B、可以通过旋转得到,故此选项错误;
C、可以通过轴对称得到,故此选项错误;
D、可通过平移得到,故此选项正确;
故选:D.
9.【解答】解:A,B,C,D四个正方体中只有C图形平移后能得到正方体W,
故选:C.
10.【解答】解:由平移的性质知,DE=AB=6cm,HE=DE﹣DH=4cm,CF=BE=3cm,HC∥DF,∠DEF=∠B=90°,
∴EC=6cm,
∴S四边形HDFC=S△EFD﹣S△ECH=DE?EF﹣EH?EC=15(cm2).
故选:C.
二.填空题(共6小题)
11.【解答】解:由题意,得草地的实际面积为:
(18﹣2)×(10﹣2)=16×8=128(m2).
故答案为128.
12.【解答】解:由平移的性质得到:图中四个小三角形的周长之和为 a+b+c.
故答案是:a+b+c.
13.【解答】解:∵将△ABC向右平移到△DEF位置,
∴BE=AD,
又∵AE=8cm,BD=2cm,
∴AD=cm.
∴△ABC移动的距离是3cm,
故答案为:3cm
14.【解答】解:所给图形的周长=3+3+4+4=14.
故答案为14.
15.【解答】解:(1)平面直角坐标系如图所示;
(2)如图所示,△A1B1C1即为所求,其中点C1的坐标为(5,2);
故答案为:(5,2);
(3)△ABC的面积是×6×(3+3)=18.
故答案为:18.
16.【解答】解:∵将直线l1沿着AB的方向平移得到直线l2,
∴AD∥BC,
∴∠1=∠2=50°.
故答案为:50°.
三.解答题(共4小题)
17.【解答】解:延长EF交AH于点M,
观察图形,得:AM+ED=BC,EF+GH+AB=CD,FG=MH,
∴垫片的周长是2BC+2CD+2 FG=2×50+2×50+2×9=218cm.
答:这块垫片的周长是218cm.
18.【解答】解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为10米,8米,
故地毯的长度为8+10=18(米),
则这块红地毯面积为:18×5=90(m2).
19.【解答】解:∵△DEF由△ABC平移而成,
∴△ABC≌△DEF,
∴图中阴影部分的面积与梯形ABEH的面积相等,
∵AB=10,DH=3,
∴EH=DE﹣DH=AB﹣DH=10﹣3=7,
∵BE=6,
∴S阴影=S梯形ABEH=(EH+AB)?BE=(10+7)×6=51.
答:阴影部分的面积为51平方厘米.
20.【解答】解:(1)由点P(x0,y0)经平移后的对应点为P1(x0+2,y0)知向右平移2个单位;
(2)如图所示,△DEF即为所求,
D(4,4)、E(2,0)、F(5,0);
(3)线段OA在平移过程中扫过的面积为2×4=8.
