高中数学北师大版必修5第1章数列1.2.2.1等差数列前n项和课件(21张)
文档属性
| 名称 | 高中数学北师大版必修5第1章数列1.2.2.1等差数列前n项和课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 642.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-21 21:08:12 | ||
图片预览







文档简介
课件21张PPT。2.2.1 等差数列的前n项和(一)
体会等差数列前n项和公式的推导过程.
熟练掌握等差数列的五个量a1,d,n,an,Sn的关系,能够由其中的三个求另外两个.
通过实例,了解等差数列前n项和公式的推导过程.
重点
理解等差数列前n项和公式推导所体现的数学思想方法.
1.2.1.2.教学目标难点复习回顾等差数列的性质:若数列 为等差数列:
(1)若 ,
则: ;(2)若
则 .(3) ==数列的前n项和的定义导思考1如何计算 ?倒
序
求
和思思考2等差数列1,2,3,…,n, …的前n项和怎么求? sn=1 + 2 + … + n-1 + n
2sn =(n+1) + (n+1) + … + (n+1) + (n+1) sn=n + n-1 + … + 2 + 1n可能是奇数也可能是偶数,怎么避免讨论?利用倒序相加法思上式相加得:由等差数列性质可知: 思考3 对于一般等差数列{an},首项为a1公差为d,如何
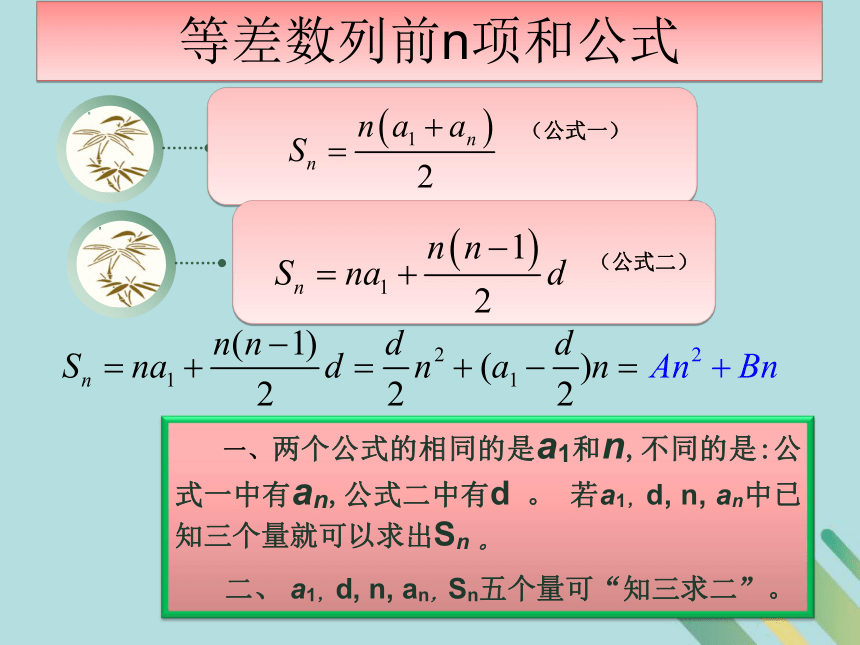
推导它的前n项和公式Sn呢?思等差数列前n项和公式 一、两个公式的相同的是a1和n,不同的是:公式一中有an,公式二中有d 。 若a1,d, n, an中已知三个量就可以求出Sn 。
二、 a1,d, n, an,Sn五个量可“知三求二”。(公式一)(公式二)探索与发现:
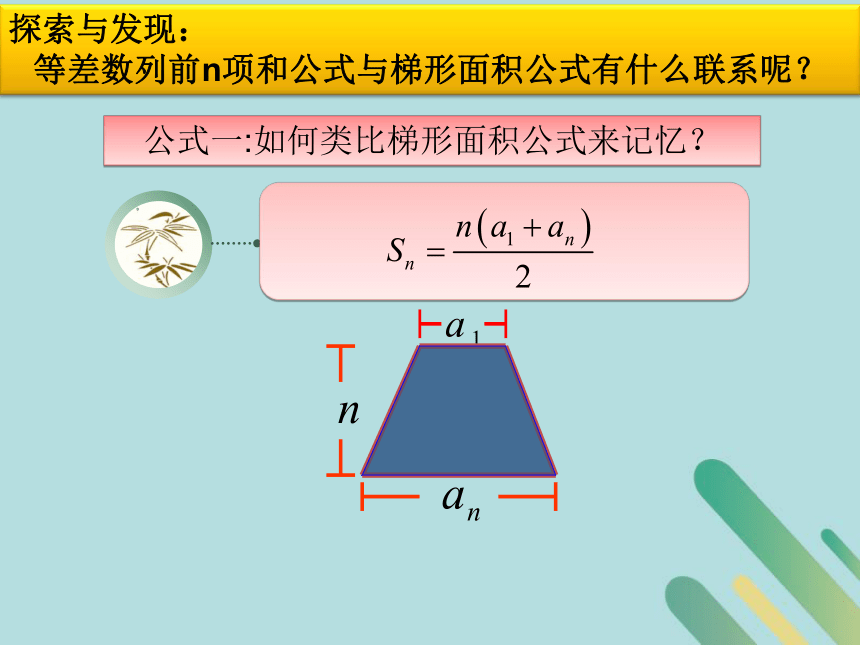
等差数列前n项和公式与梯形面积公式有什么联系呢?公式一:如何类比梯形面积公式来记忆?分割成一个平行四边形和一个三角形公式二:如何类比梯形面积公式来记忆? 例1 根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=50议展 例2、已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件可以确定这个等差数列的前n项和的公式吗?议展
用公式二做做方法1方法2用公式一做做解析: ,可用通项公式与前n项和关系解决.当n=1时,例3 设数列 前n项和 ,则数列
{an}的通项公式为____________.当 时, 也适合 ,所以议展解析: ,可用通项公式与前n项和关系解决.当n=1时,例4 设数列 前n项和 ,则数列
{an}的通项公式为____________.当 时, 不适合 ,所以议展例5 判断下列说法的真假:
(1)数列{an}为等差数列的条件是其前n项和Sn为一个关于n的二次函数;
(2)若一个数列{an}的前n项和Sn=3n,不是关于n的二次函数式,那么{an}不是等差数列;
(3)若一个数列{an}的前n项和Sn=2n2-n+1是关于n的二次函数式,那么{an}是等差数列.规律总结:数列 为等差数列 ,(A,B为常数) . 假,注意公差为零时的情况。假,注意公差为零时的情况。假,二次式的常数项要为0例6 设Sn数列{an}的前n项的和,已知a1=1,an=Sn?Sn-1,(n≥2),
则 Sn=______________.方法总结:在Sn和an混合的已知式中,常根据待求的东西去决定
是将Sn换为an,还是将an换为Sn.议展 1.在等差数列{an}中,
(1)a1=105,an=994,d=7,求Sn;
(2)a1=1,S2=a3,求a2 ,Sn.
[思路探索] 将等差数列问题利用化归思想转化为基本量的关系,再利用方程的思想来解决,是通性通法.
解 (1)由an=a1+(n-1)d,且a1=105,d=7,得
994=105+(n-1)×7,解之得n=128.(2) 由已知 得 检(1)已知 ,求 2 .在等差数列 中:(2)已知等差数列 的前4项的和为25,后4项的和为63,前n项的和为286,求项数n. 解:(1)又 (2)而检课时小结:1等差数列{an}的前n项和的计算公式为:
2判断数列为等差数列的方法:
(1)定义法:an+1-an=d,或an-an-1=d(d为常数);
(2)等差中项法:2an+1=an+an+2;
(3)通项法:an=pn+q;
(4)前n项和法:Sn=An2+Bn.
体会等差数列前n项和公式的推导过程.
熟练掌握等差数列的五个量a1,d,n,an,Sn的关系,能够由其中的三个求另外两个.
通过实例,了解等差数列前n项和公式的推导过程.
重点
理解等差数列前n项和公式推导所体现的数学思想方法.
1.2.1.2.教学目标难点复习回顾等差数列的性质:若数列 为等差数列:
(1)若 ,
则: ;(2)若
则 .(3) ==数列的前n项和的定义导思考1如何计算 ?倒
序
求
和思思考2等差数列1,2,3,…,n, …的前n项和怎么求? sn=1 + 2 + … + n-1 + n
2sn =(n+1) + (n+1) + … + (n+1) + (n+1) sn=n + n-1 + … + 2 + 1n可能是奇数也可能是偶数,怎么避免讨论?利用倒序相加法思上式相加得:由等差数列性质可知: 思考3 对于一般等差数列{an},首项为a1公差为d,如何
推导它的前n项和公式Sn呢?思等差数列前n项和公式 一、两个公式的相同的是a1和n,不同的是:公式一中有an,公式二中有d 。 若a1,d, n, an中已知三个量就可以求出Sn 。
二、 a1,d, n, an,Sn五个量可“知三求二”。(公式一)(公式二)探索与发现:
等差数列前n项和公式与梯形面积公式有什么联系呢?公式一:如何类比梯形面积公式来记忆?分割成一个平行四边形和一个三角形公式二:如何类比梯形面积公式来记忆? 例1 根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=50议展 例2、已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件可以确定这个等差数列的前n项和的公式吗?议展
用公式二做做方法1方法2用公式一做做解析: ,可用通项公式与前n项和关系解决.当n=1时,例3 设数列 前n项和 ,则数列
{an}的通项公式为____________.当 时, 也适合 ,所以议展解析: ,可用通项公式与前n项和关系解决.当n=1时,例4 设数列 前n项和 ,则数列
{an}的通项公式为____________.当 时, 不适合 ,所以议展例5 判断下列说法的真假:
(1)数列{an}为等差数列的条件是其前n项和Sn为一个关于n的二次函数;
(2)若一个数列{an}的前n项和Sn=3n,不是关于n的二次函数式,那么{an}不是等差数列;
(3)若一个数列{an}的前n项和Sn=2n2-n+1是关于n的二次函数式,那么{an}是等差数列.规律总结:数列 为等差数列 ,(A,B为常数) . 假,注意公差为零时的情况。假,注意公差为零时的情况。假,二次式的常数项要为0例6 设Sn数列{an}的前n项的和,已知a1=1,an=Sn?Sn-1,(n≥2),
则 Sn=______________.方法总结:在Sn和an混合的已知式中,常根据待求的东西去决定
是将Sn换为an,还是将an换为Sn.议展 1.在等差数列{an}中,
(1)a1=105,an=994,d=7,求Sn;
(2)a1=1,S2=a3,求a2 ,Sn.
[思路探索] 将等差数列问题利用化归思想转化为基本量的关系,再利用方程的思想来解决,是通性通法.
解 (1)由an=a1+(n-1)d,且a1=105,d=7,得
994=105+(n-1)×7,解之得n=128.(2) 由已知 得 检(1)已知 ,求 2 .在等差数列 中:(2)已知等差数列 的前4项的和为25,后4项的和为63,前n项的和为286,求项数n. 解:(1)又 (2)而检课时小结:1等差数列{an}的前n项和的计算公式为:
2判断数列为等差数列的方法:
(1)定义法:an+1-an=d,或an-an-1=d(d为常数);
(2)等差中项法:2an+1=an+an+2;
(3)通项法:an=pn+q;
(4)前n项和法:Sn=An2+Bn.
