高中数学第2章解三角形2.1.1正弦定理课件北师大版必修5(18张)
文档属性
| 名称 | 高中数学第2章解三角形2.1.1正弦定理课件北师大版必修5(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 707.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-21 00:00:00 | ||
图片预览





文档简介
课件18张PPT。ABC§2.1.1 正弦定理导
1.在△ABC中,三个角A,B,C的对边分别为a,b,c:
(1)角的关系为__________________;
(2)边的关系为__________________;
(3)边角关系为__________________.A+B+C=πa+b>c,a-b<c大角对大边导2.在Rt△ABC中的有关定理或结论
在Rt△ABC中,若C=90°,则有:
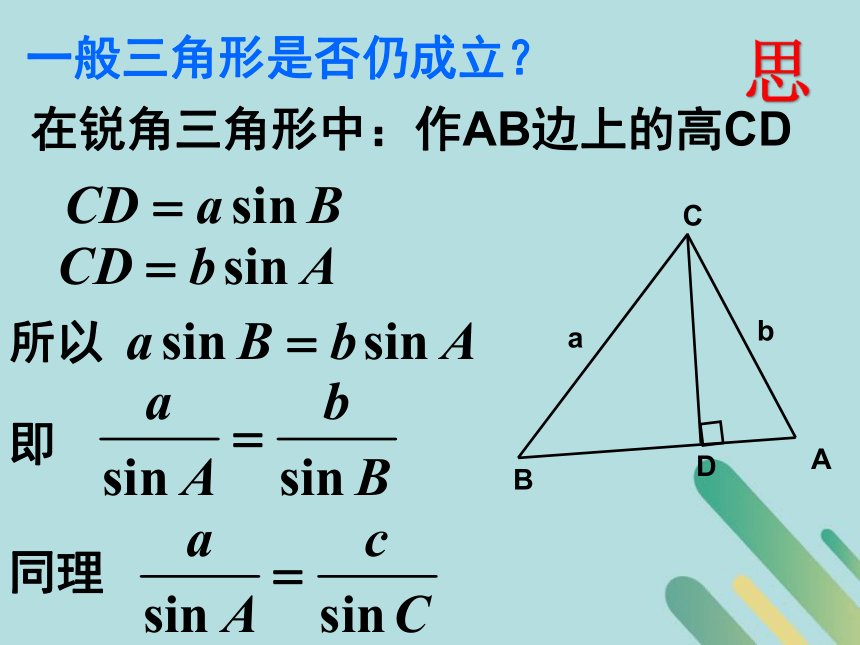
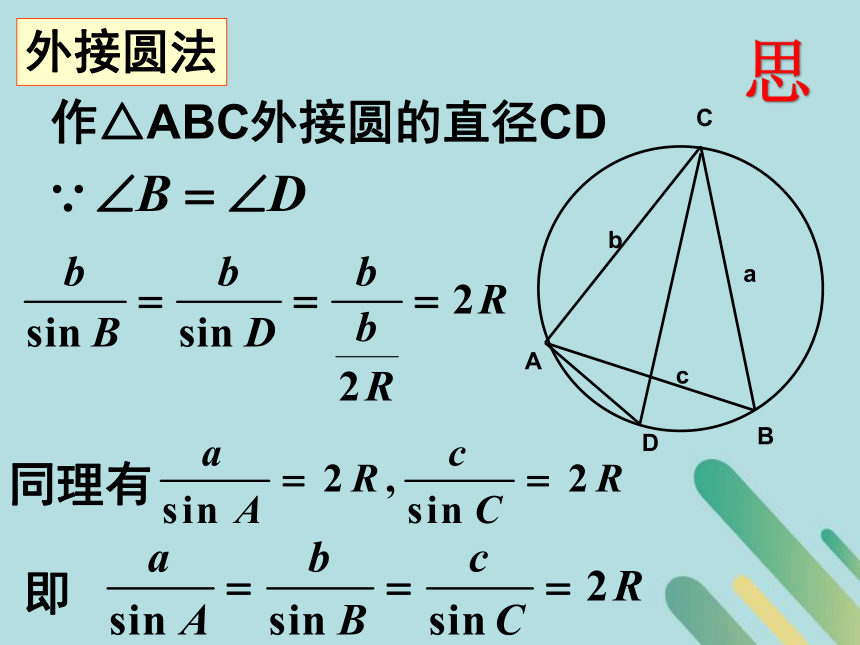
(1)A+B= ,0°(2)a2+b2=c2(勾股定理);导90°ccc一般三角形是否仍成立?D在锐角三角形中:作AB边上的高CD所以即同理思D在钝角三角形中:作AB边上的高CD即所以外接圆法D作△ABC外接圆的直径CD同理有即思面积法.O解:如图建立直角坐标系.过C点作CD?AB于D.D则点C的坐标(bcosA,bsinA)(bcosA,bsinA)于是△ABC的面积S△=同样可得S△=思同除以 , 得即解 已知两角及一边解三角形 ——正弦定理 探究一 正弦定理在解三角形中的应用议议已知两边及一边的对角解三角形
【例2】已知下列各三角形的两边及其一边的对角,解 三角形.
一个解议解两个解议无解正弦定理可实现三角形中边角的相互转化:
(1)已知两角和任一边,求其它两边和一角.
(2)已知两边和其中一边的对角,求另一边和两角.
议解三角形面积公式:探究二 用正弦定理求有关三角形的面积问题议解:议解议探究三 用正弦定理判断三角形的形状解议
1.在△ABC中,三个角A,B,C的对边分别为a,b,c:
(1)角的关系为__________________;
(2)边的关系为__________________;
(3)边角关系为__________________.A+B+C=πa+b>c,a-b<c大角对大边导2.在Rt△ABC中的有关定理或结论
在Rt△ABC中,若C=90°,则有:
(1)A+B= ,0°
【例2】已知下列各三角形的两边及其一边的对角,解 三角形.
一个解议解两个解议无解正弦定理可实现三角形中边角的相互转化:
(1)已知两角和任一边,求其它两边和一角.
(2)已知两边和其中一边的对角,求另一边和两角.
议解三角形面积公式:探究二 用正弦定理求有关三角形的面积问题议解:议解议探究三 用正弦定理判断三角形的形状解议
