高中数学第一章立体几何初步1.4空间图形的基本关系与公理课件北师大版必修2(20张)
文档属性
| 名称 | 高中数学第一章立体几何初步1.4空间图形的基本关系与公理课件北师大版必修2(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 333.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-21 00:00:00 | ||
图片预览




文档简介
课件20张PPT。空间图形的公理思考:1、直线l上有一个点P在平面α内,直线l 是否全部落在平面α内?
2、直线l上有两个点P、Q在平面α内, 直线l是否全部落在平面α内?二、平面的基本性质 若一条直线的两点在一个平面内,则这条直线上所有的点都在这个平面内公理1AB即:思考2:请你用尺子做实验并回答以下问题(分组讨论)
1、过一点有几个平面?
2、过两点有几个平面?
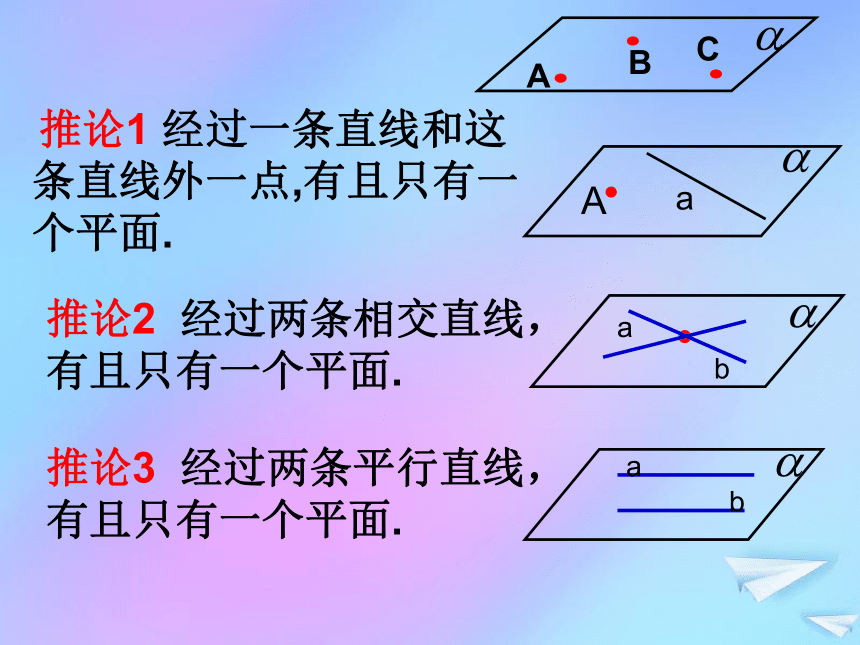
3、过三点有几个平面?不共线三点确定一个平面 经过不在同一条直线上的三点,有且只有一个平面。 公理2 推论1 ?Aa 经过一条直线和这
条直线外一点,有且只有一
个平面.推论2 ?经过两条相交直线,
有且只有一个平面.推论3 ?经过两条平行直线,
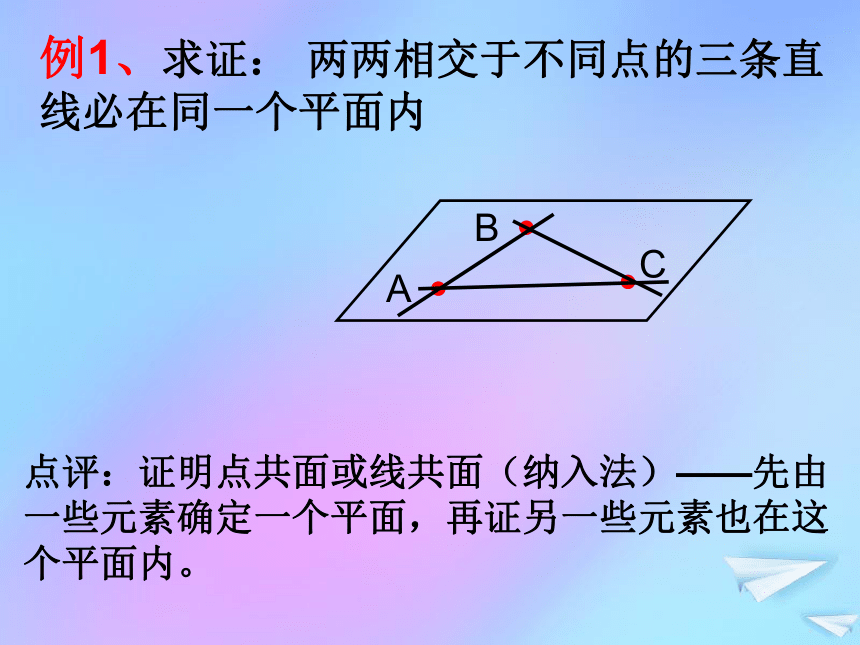
有且只有一个平面.baabABC例1、求证: ?两两相交于不同点的三条直
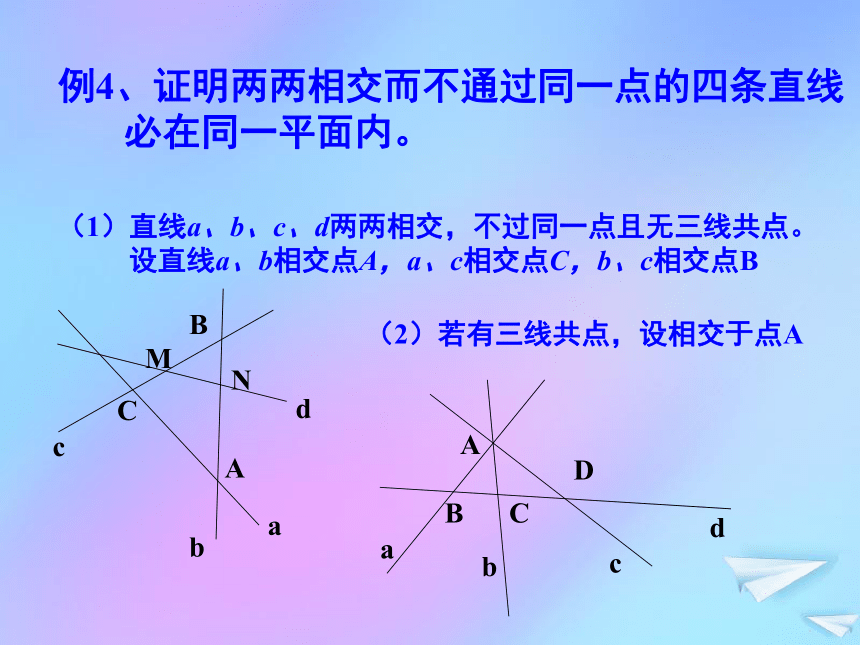
线必在同一个平面内点评:证明点共面或线共面(纳入法)——先由一些元素确定一个平面,再证另一些元素也在这个平面内。例4、证明两两相交而不通过同一点的四条直线
必在同一平面内。(1)直线a、b、c、d两两相交,不过同一点且无三线共点。
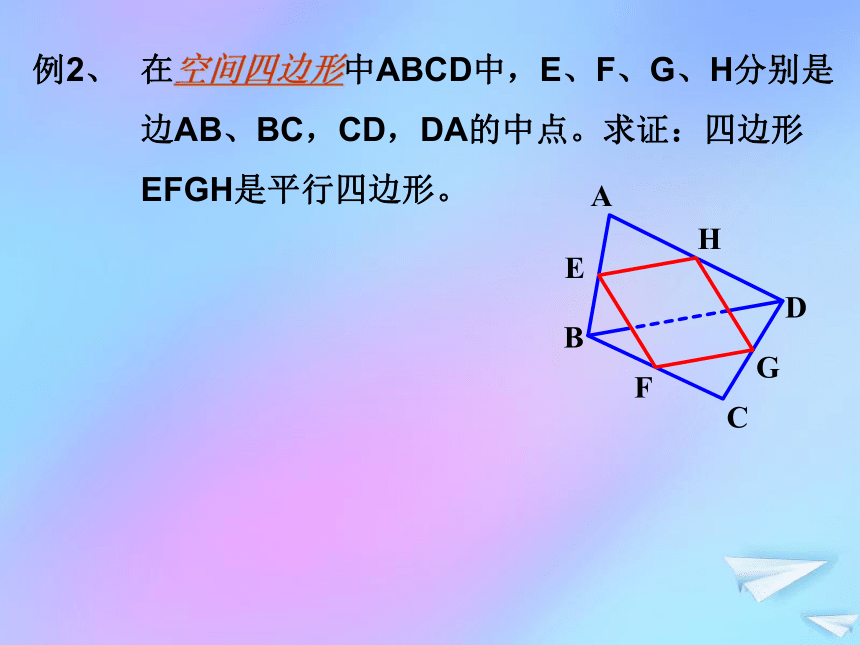
设直线a、b相交点A,a、c相交点C,b、c相交点B(2)若有三线共点,设相交于点A例2、在空间四边形中ABCD中,E、F、G、H分别是
边AB、BC,CD,DA的中点。求证:四边形
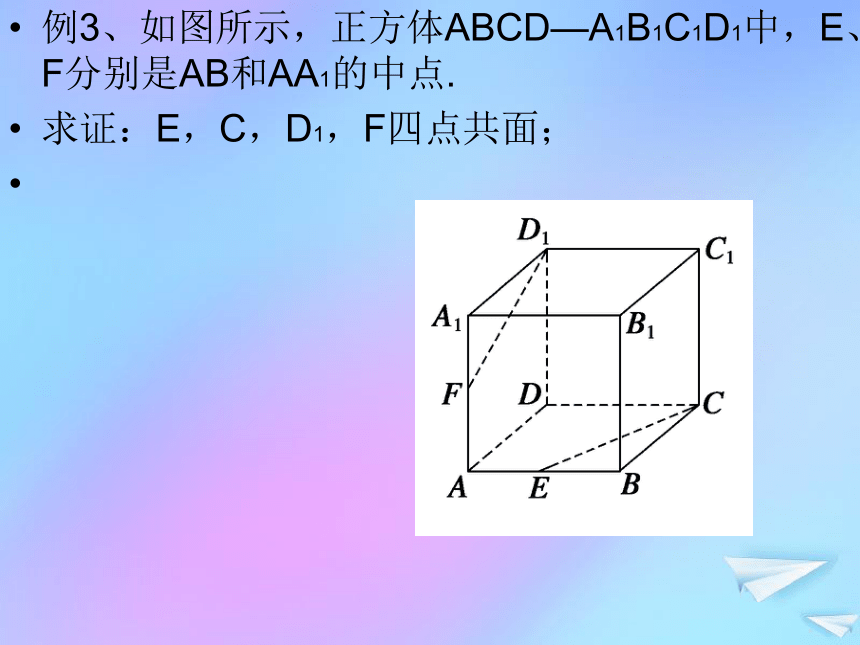
EFGH是平行四边形。例3、如图所示,正方体ABCD—A1B1C1D1中,E、F分别是AB和AA1的中点.
求证:E,C,D1,F四点共面;
例7、
如图,在正方体 中, 为 上的中点,画出平面 与平面 的交线。 例4、空间四边形ABCD中,E、F、G、H、M、N分别是棱AB、BC、CD、DA、AC、BD的中点
求证: EG、FH、MN共点探讨1:若3条直线相交于一点时,则这3条直线确定几个平面?如果4条直线相交于一点呢?(1)3条直线共面时(2)每2条直线确定
一平面时(1)4条直线 全共面时(2)有3条直线共面时(3)每2条直线都确定一平面时思考3:把三角板的一个角立在课桌上,三角板所在平面与桌面所在平面是否只相交与一点B?为什么?B公理3 若两个平面有一个公共点,则它们还有其他公共点,这些公共点的集合是 一条过这个公共点的直线即:证明:(公理2)同理可证:点评:证明点共线——证明这些点同时在两相交平面内ABCPRQ例6、如图所示,正方体ABCD—A1B1C1D1中,E、F分别是AB和AA1的中点.
求证: CE,D1F,DA三线共点. 点评:证明线共点——先确定两条直线交点,
再证交点在第三条直线上。探讨2:3个平面可将空间分成几部分?(2)(3)(4)(5)例8、正方体ABCD-A1B1C1D1中,对角线A1C与平面BDC1交于O,AC、BD交于点M.
求证:点C1、O、M共线.平面的基本性质公理1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
公理2:经过不在同一条直线上的三点有且只有一个平面。推论1:经过一条直线和这条直线外的一点有且只有一个平面。推论2: 经过两条相交直线有且只有一个平面。 推论3:经过两条平行直线有且只有一个平面。基本题型证明线共点:先确定两条直线交点,再证交点在第三条直线上。证明点共线:证明这些点同时在两相交平面内证明点共面或线共面:先由一些元素确定一个平面,再证另一些元素也在这个平面内。
2、直线l上有两个点P、Q在平面α内, 直线l是否全部落在平面α内?二、平面的基本性质 若一条直线的两点在一个平面内,则这条直线上所有的点都在这个平面内公理1AB即:思考2:请你用尺子做实验并回答以下问题(分组讨论)
1、过一点有几个平面?
2、过两点有几个平面?
3、过三点有几个平面?不共线三点确定一个平面 经过不在同一条直线上的三点,有且只有一个平面。 公理2 推论1 ?Aa 经过一条直线和这
条直线外一点,有且只有一
个平面.推论2 ?经过两条相交直线,
有且只有一个平面.推论3 ?经过两条平行直线,
有且只有一个平面.baabABC例1、求证: ?两两相交于不同点的三条直
线必在同一个平面内点评:证明点共面或线共面(纳入法)——先由一些元素确定一个平面,再证另一些元素也在这个平面内。例4、证明两两相交而不通过同一点的四条直线
必在同一平面内。(1)直线a、b、c、d两两相交,不过同一点且无三线共点。
设直线a、b相交点A,a、c相交点C,b、c相交点B(2)若有三线共点,设相交于点A例2、在空间四边形中ABCD中,E、F、G、H分别是
边AB、BC,CD,DA的中点。求证:四边形
EFGH是平行四边形。例3、如图所示,正方体ABCD—A1B1C1D1中,E、F分别是AB和AA1的中点.
求证:E,C,D1,F四点共面;
例7、
如图,在正方体 中, 为 上的中点,画出平面 与平面 的交线。 例4、空间四边形ABCD中,E、F、G、H、M、N分别是棱AB、BC、CD、DA、AC、BD的中点
求证: EG、FH、MN共点探讨1:若3条直线相交于一点时,则这3条直线确定几个平面?如果4条直线相交于一点呢?(1)3条直线共面时(2)每2条直线确定
一平面时(1)4条直线 全共面时(2)有3条直线共面时(3)每2条直线都确定一平面时思考3:把三角板的一个角立在课桌上,三角板所在平面与桌面所在平面是否只相交与一点B?为什么?B公理3 若两个平面有一个公共点,则它们还有其他公共点,这些公共点的集合是 一条过这个公共点的直线即:证明:(公理2)同理可证:点评:证明点共线——证明这些点同时在两相交平面内ABCPRQ例6、如图所示,正方体ABCD—A1B1C1D1中,E、F分别是AB和AA1的中点.
求证: CE,D1F,DA三线共点. 点评:证明线共点——先确定两条直线交点,
再证交点在第三条直线上。探讨2:3个平面可将空间分成几部分?(2)(3)(4)(5)例8、正方体ABCD-A1B1C1D1中,对角线A1C与平面BDC1交于O,AC、BD交于点M.
求证:点C1、O、M共线.平面的基本性质公理1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
公理2:经过不在同一条直线上的三点有且只有一个平面。推论1:经过一条直线和这条直线外的一点有且只有一个平面。推论2: 经过两条相交直线有且只有一个平面。 推论3:经过两条平行直线有且只有一个平面。基本题型证明线共点:先确定两条直线交点,再证交点在第三条直线上。证明点共线:证明这些点同时在两相交平面内证明点共面或线共面:先由一些元素确定一个平面,再证另一些元素也在这个平面内。
