六年级下册数学一课一练-5.15立体图形 浙教版(含答案)
文档属性
| 名称 | 六年级下册数学一课一练-5.15立体图形 浙教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 73.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-22 00:00:00 | ||
图片预览



文档简介
六年级下册数学一课一练-5.15立体图形
一、单选题
1.正方体有(?? )个顶点。
A.?6?????????????????????????????????????????????/B.?12?????????????????????????????????????????????/C.?8
2.下列有 /的图形的立体图形是(?? )。
A.?/?????????????????????????????/B.?/?????????????????????????????/C.?/
3.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上下面(?? )圆形铁片正好可以做成圆柱形容器.
A.?无法计算????????????????????????B.?d=3厘米????????????????????????C.?r=4厘米????????????????????????D.?d=6厘米或8厘米
4.正方体是特殊的( ??)。
A.?长方体??????????????????????????????????/B.?圆柱体??????????????????????????????????/C.?球??????????????????????????????????/D.?圆锥体
5.下面图形中,是正方体的是(? )
A.?/?????????????????????????/B.?/?????????????????????????/C.?/?????????????????????????/D.?/
6.把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是(? )立方分米.
A.?200.96??????????????????????????????????/B.?100.48??????????????????????????????????/C.?64??????????????????????????????????/D.?50.24
7.一个棱长是4分米的正方体,棱长总和是(?? )分米。
A.?24????????????????????????????????????????????/B.?32????????????????????????????????????????????/C.?48
二、判断题
8.圆柱的体积等于圆锥体积的3倍。
9.圆锥的体积等于圆柱体积的 /
10.圆锥的底面积扩大到原来的3倍,高不变,体积扩大到原来的3倍。
11.圆柱体的高扩大3倍,体积就扩大3倍.
12.长方体中除了相对的面完全相同,也有可能有两个相邻的面完全相同。
三、填空题
13.在一个长方体的顶点上相交了________条棱,这三条棱的长度分别叫作长方体的________、________、________
14.一个圆锥的底面半径扩大2倍,高扩大3倍,它的体积就扩大________倍.
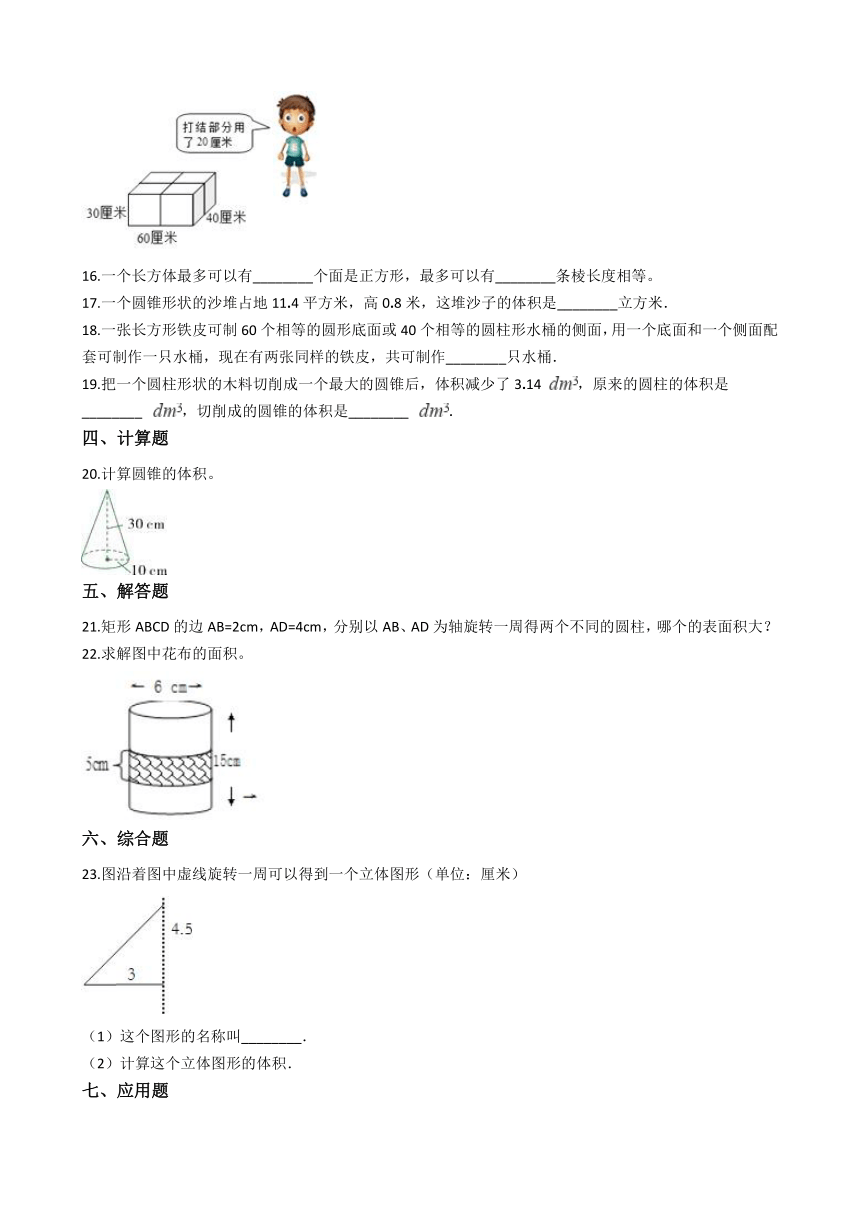
15.如图,绳子的长是________厘米.
/
16.一个长方体最多可以有________个面是正方形,最多可以有________条棱长度相等。
17.一个圆锥形状的沙堆占地11.4平方米,高0.8米,这堆沙子的体积是________立方米.
18.一张长方形铁皮可制60个相等的圆形底面或40个相等的圆柱形水桶的侧面,用一个底面和一个侧面配套可制作一只水桶,现在有两张同样的铁皮,共可制作________只水桶.
19.把一个圆柱形状的木料切削成一个最大的圆锥后,体积减少了3.14 /,原来的圆柱的体积是________? /,切削成的圆锥的体积是________? /.
四、计算题
20.计算圆锥的体积。
/
五、解答题
21.矩形ABCD的边AB=2cm,AD=4cm,分别以AB、AD为轴旋转一周得两个不同的圆柱,哪个的表面积大?
22.求解图中花布的面积。
/
六、综合题
23.图沿着图中虚线旋转一周可以得到一个立体图形(单位:厘米)
/
(1)这个图形的名称叫________.
(2)计算这个立体图形的体积.
七、应用题
24.一个油桶的底面是圆形,把这个油桶放到在地面上滚动一圈的距离是2.512米,这个油桶的底面积是多少?
25.如图,把一个高为12厘米的圆柱切成若干等份,拼成一个近似的长方体.表面积比原来增加48平方厘米,那么圆柱体积是多少立方厘米? /
答案解析部分
一、单选题
1.【答案】C
【解析】【解答】解:根据正方体的特征可知,正方体有8个顶点. 故答案为:C
【分析】正方体有12条棱,12条棱的长度都相等;正方体有6个完全相同的正方形的面;正方体有8个顶点.
2.【答案】C
【解析】【解答】由正方形的立体图形是正方体,故选:C.
【分析】这道题主要考查了学生对立体图形的特征的掌握情况.解答此题的关键是根据立体图形的基本特征进行选择.
3.【答案】D
【解析】【解答】解:25.12÷3.14=8(厘米),
18.84÷3.14=6(厘米),
答:可以配上直径6厘米或8厘米的圆形铁片正好做成圆柱形容器.
故选:D.
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长、宽等于圆柱的高,根据圆的周长公式:c=πd,那么d=c÷π,据此求出直径,问题即可得到解决.
4.【答案】A
【解析】【解答】解:根据正方体的特征可知,正方体是特殊的长方体. 故答案为:A
【分析】正方体可以看做是长、宽、高都相等的长方体,因此正方体是特殊的长方体.
5.【答案】A
【解析】【解答】解:A是正方体,B是长方体,C是正方形,D是棱台;
故选:A.
【分析】依据正方体的特征:正方体有六个面,十二条棱,八个顶点,它是由六个正方形围成的立体图形,所有的面完全相同,十二条棱长短完全相同.据此即可判断.
6.【答案】D
【解析】【解答】解:3.14(4÷2)2×4
=3.14×4×4
=50.24(立方分米)
答:圆柱的体积是50.24立方分米.
故选:D.
【分析】正方体内削出的最大圆柱的底面直径和高都等于这个正方体的棱长,由此利用圆柱的体积公式即可解答.此题考查了圆柱的体积公式的计算应用,抓住正方体内最大的圆柱的特点得出圆柱的底面直径和高是解决此类问题的关键.
7.【答案】C
【解析】【解答】4×12=48(分米)
【分析】正方体总共有12条棱,并且每条棱的长度都是一样,所以知道了每条棱的长度,就用4分米乘以12即可。
二、判断题
8.【答案】错误
【解析】【解答】等底等高的圆柱的体积等于圆锥体积的3倍,原题说法错误. 故答案为:错误.
【分析】一个圆柱的体积是与它等底等高的圆锥体积的3倍,原题没有注明“等底等高”或其它的条件,只说“圆柱的体积是圆锥体积的3倍”是错误的,据此判断.
9.【答案】错误
【解析】【解答】解:圆锥的体积等于与之等底等高的圆柱体积的/。 故答案为:错误。
【分析】圆锥的体积等于与之等底等高的圆柱体积的/
10.【答案】正确
【解析】【解答】解:根据圆锥的体积公式可知,圆锥的底面积扩大到原来的3倍,高不变,体积扩大到原来的3倍,原题说法正确. 故答案为:正确
【分析】圆锥的体积=底面积×高×/,所以圆锥体积扩大的倍数与底面积扩大的倍数相等.
11.【答案】错误
【解析】【解答】解:因为圆柱的体积是由它的底面积和高两个条件决定的,圆柱的高扩大3倍,它的底面积是否变化没有确定,所以它的体积也无法确定.
因此,圆柱体的高扩大3倍,体积就扩大3倍.此说法是错误的.
故答案为:错误.
【分析】根据圆柱的体积公式:v=sh,圆柱的体积是由它的底面积和高两个条件决定的,圆柱的高扩大3倍,它的底面积是否变化没有确定,所以它的体积也无法确定.
12.【答案】正确
【解析】【解答】解:长方体中除了相对的面完全相同,特殊情况下有2个相对的面是正方形,剩下的4个面是长方形,这四个面也是完全相同的,所以说长方体也有可能有两个相邻的面完全相同.原题说法正确. 故答案为:正确
【分析】特殊的长方体有两个正方形的面,另外的四个面是完全相同的长方形,这样的长方体就有两个相邻的面完全相同.
三、填空题
13.【答案】3;长;宽;高
【解析】【解答】在一个长方体的顶点上相交了3条棱,这三条棱的长度分别叫作长方体的长、宽、高. 故答案为:3;长;宽;高.
【分析】根据对长方体的认识可知,我们把相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高,习惯上,把水平方向的棱的长度作为长,把前后方向棱的长度作为宽,竖着的棱的长度作为高,据此解答.
14.【答案】12
【解析】【解答】解:圆锥的底面半径扩大2倍,它的底面积就扩大2×2=4倍,圆锥的高扩大3倍,那么圆锥的体积就扩大4×3=12倍.
答:它的体积扩大12倍.故答案为:12.
【分析】根据圆锥的体积公式:v=/sh,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此解答.
15.【答案】340
【解析】【解答】解:(60+40+)×2+30×4+20=100×2+120+20=340厘米;
答:绳子的长是340厘米.
故答案为:340.
【分析】由图可以观察,绳子的长度是2个长宽的长度和4个高的长度以及打结部分构成,由此即可解决问题.
16.【答案】2;8
【解析】【解答】如图:一个长方体最多可以有 2 个面是正方形,最多可以有 8 条棱长度相等。 / 【分析】有2个面是正方形的长方体,也是比较特殊的,最多可以有8条棱长度相等。
17.【答案】3.04
【解析】【解答】11.4×0.8×/ =9.12×/ =3.04(立方米) 故答案为:3.04
【分析】已知圆锥的底面积和高,求圆锥的体积,用公式:V=/Sh,据此列式解答.
18.【答案】48
【解析】【解答】解:2÷( /+ /),
=2÷ /,
=48(只);
答:共可制作48只水桶.
【分析】此题如果两张结合不会多产生下脚料话(一张铁皮制40个圆形底面后,还可以制底面加相同数量的侧面),可以用分数应用题的思路解答.把一张铁皮看做整体“1”,则一个圆形底面占1/60,一个侧面占1/40.然后根据题意列式解答即可.此题重点考查分数应用题与圆柱的展开图.
19.【答案】4.71;1.57
【解析】【解答】3.14÷(1-/)=4.71(立方分米),4.71×/=1.57(立方分米)
【分析】解答此题要明确等底等高的圆柱的体积等于圆锥体积的3倍,已知体积减少3.14立方分米,那么减少的部分是圆柱体积的(1-/),然后根据分数除法的意义求出圆柱的体积,再用圆柱的体积乘/就是圆锥的体积。
四、计算题
20.【答案】解:3.14×102×30×/ =3.14×100×10 =3140(cm2)
【解析】【分析】圆锥的体积=底面积×高×/,由此根据圆锥的体积公式计算即可.
五、解答题
21.【答案】解:以AB为轴,AD为底面半径时,底面积是最大的,所以AB为轴的表面积大.
【解析】【分析】圆柱的侧面积就是这个矩形的面积,所以圆柱的侧面积是不变的,那么底面积大的表面积就大,所以以AD为底面半径旋转后得到的圆柱的表面积最大.
22.【答案】解:由题意可知,所求花布的面积实际是求该圆柱5cm高的侧面积,
侧面展开图中,长方形的长即底面周长为:πd=6×3.14=18.84(cm)
长方形的宽即花布所围成圆柱的高为:5cm
则花布的面积为:S=Ch=18.84×5=94.2(cm2)
【解析】【分析】根据图意可知,要求花布的面积,就是求高5cm的圆柱的侧面积,先求出圆柱的底面周长,用公式:C=πd,然后用圆柱侧面积公式:S=Ch,据此列式解答.
六、综合题
23.【答案】(1)圆锥 (2)解:圆锥的体积= /×3.14×32×4.5
= /×3.14×9×4.5
=9.42×4.5
=42.39(立方厘米);
答:这个立体图形的体积是42.39立方厘米.
【解析】【解答】解:(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这个立体图形叫做圆锥.
【分析】(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这个立体图形叫做圆锥.(2)圆锥的体积= /×底面积×高,圆锥的底面半径和高已知,从而可以求出圆锥的体积.
七、应用题
24.【答案】解:3.14×(2.512÷3.14÷2)2 =3.14×0.42 =3.14×0.16 =0.5024(平方米), 答:这个油桶的底面积是0.5024平方米
【解析】【分析】把这个油桶放到在地面上滚动一圈的距离是2.512米,也就是油桶的底面周长是2.512米,根据圆的周长公式:c=2πr,求出底面半径,再根据圆的面积公式:s=πr2 , 把数据代入公式解答即可.此题主要考查圆的周长公式、面积公式在实际生活中的应用.
25.【答案】解:底面半径:48÷2÷12=2(厘米); 圆柱体积:3.14×22×12=150.72(立方厘米); 答:圆柱的体积是150.72立方厘米.
【解析】【分析】将一个圆柱切开后拼成一个近似的长方体,高没变,但拼成的长方体表面积比圆柱多了两个长方形的面积,这两个长方形的长都和圆柱的高相等,都是12厘米,宽都和圆柱的底面半径相等;已知表面积增加了48平方厘米,就可求出底面半径是多少厘米,进而再求出圆柱的体积即可.此题是求圆柱的体积,必须先知道底面半径和高,才可利用“V=Sh”来解答.
一、单选题
1.正方体有(?? )个顶点。
A.?6?????????????????????????????????????????????/B.?12?????????????????????????????????????????????/C.?8
2.下列有 /的图形的立体图形是(?? )。
A.?/?????????????????????????????/B.?/?????????????????????????????/C.?/
3.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上下面(?? )圆形铁片正好可以做成圆柱形容器.
A.?无法计算????????????????????????B.?d=3厘米????????????????????????C.?r=4厘米????????????????????????D.?d=6厘米或8厘米
4.正方体是特殊的( ??)。
A.?长方体??????????????????????????????????/B.?圆柱体??????????????????????????????????/C.?球??????????????????????????????????/D.?圆锥体
5.下面图形中,是正方体的是(? )
A.?/?????????????????????????/B.?/?????????????????????????/C.?/?????????????????????????/D.?/
6.把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是(? )立方分米.
A.?200.96??????????????????????????????????/B.?100.48??????????????????????????????????/C.?64??????????????????????????????????/D.?50.24
7.一个棱长是4分米的正方体,棱长总和是(?? )分米。
A.?24????????????????????????????????????????????/B.?32????????????????????????????????????????????/C.?48
二、判断题
8.圆柱的体积等于圆锥体积的3倍。
9.圆锥的体积等于圆柱体积的 /
10.圆锥的底面积扩大到原来的3倍,高不变,体积扩大到原来的3倍。
11.圆柱体的高扩大3倍,体积就扩大3倍.
12.长方体中除了相对的面完全相同,也有可能有两个相邻的面完全相同。
三、填空题
13.在一个长方体的顶点上相交了________条棱,这三条棱的长度分别叫作长方体的________、________、________
14.一个圆锥的底面半径扩大2倍,高扩大3倍,它的体积就扩大________倍.
15.如图,绳子的长是________厘米.
/
16.一个长方体最多可以有________个面是正方形,最多可以有________条棱长度相等。
17.一个圆锥形状的沙堆占地11.4平方米,高0.8米,这堆沙子的体积是________立方米.
18.一张长方形铁皮可制60个相等的圆形底面或40个相等的圆柱形水桶的侧面,用一个底面和一个侧面配套可制作一只水桶,现在有两张同样的铁皮,共可制作________只水桶.
19.把一个圆柱形状的木料切削成一个最大的圆锥后,体积减少了3.14 /,原来的圆柱的体积是________? /,切削成的圆锥的体积是________? /.
四、计算题
20.计算圆锥的体积。
/
五、解答题
21.矩形ABCD的边AB=2cm,AD=4cm,分别以AB、AD为轴旋转一周得两个不同的圆柱,哪个的表面积大?
22.求解图中花布的面积。
/
六、综合题
23.图沿着图中虚线旋转一周可以得到一个立体图形(单位:厘米)
/
(1)这个图形的名称叫________.
(2)计算这个立体图形的体积.
七、应用题
24.一个油桶的底面是圆形,把这个油桶放到在地面上滚动一圈的距离是2.512米,这个油桶的底面积是多少?
25.如图,把一个高为12厘米的圆柱切成若干等份,拼成一个近似的长方体.表面积比原来增加48平方厘米,那么圆柱体积是多少立方厘米? /
答案解析部分
一、单选题
1.【答案】C
【解析】【解答】解:根据正方体的特征可知,正方体有8个顶点. 故答案为:C
【分析】正方体有12条棱,12条棱的长度都相等;正方体有6个完全相同的正方形的面;正方体有8个顶点.
2.【答案】C
【解析】【解答】由正方形的立体图形是正方体,故选:C.
【分析】这道题主要考查了学生对立体图形的特征的掌握情况.解答此题的关键是根据立体图形的基本特征进行选择.
3.【答案】D
【解析】【解答】解:25.12÷3.14=8(厘米),
18.84÷3.14=6(厘米),
答:可以配上直径6厘米或8厘米的圆形铁片正好做成圆柱形容器.
故选:D.
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长、宽等于圆柱的高,根据圆的周长公式:c=πd,那么d=c÷π,据此求出直径,问题即可得到解决.
4.【答案】A
【解析】【解答】解:根据正方体的特征可知,正方体是特殊的长方体. 故答案为:A
【分析】正方体可以看做是长、宽、高都相等的长方体,因此正方体是特殊的长方体.
5.【答案】A
【解析】【解答】解:A是正方体,B是长方体,C是正方形,D是棱台;
故选:A.
【分析】依据正方体的特征:正方体有六个面,十二条棱,八个顶点,它是由六个正方形围成的立体图形,所有的面完全相同,十二条棱长短完全相同.据此即可判断.
6.【答案】D
【解析】【解答】解:3.14(4÷2)2×4
=3.14×4×4
=50.24(立方分米)
答:圆柱的体积是50.24立方分米.
故选:D.
【分析】正方体内削出的最大圆柱的底面直径和高都等于这个正方体的棱长,由此利用圆柱的体积公式即可解答.此题考查了圆柱的体积公式的计算应用,抓住正方体内最大的圆柱的特点得出圆柱的底面直径和高是解决此类问题的关键.
7.【答案】C
【解析】【解答】4×12=48(分米)
【分析】正方体总共有12条棱,并且每条棱的长度都是一样,所以知道了每条棱的长度,就用4分米乘以12即可。
二、判断题
8.【答案】错误
【解析】【解答】等底等高的圆柱的体积等于圆锥体积的3倍,原题说法错误. 故答案为:错误.
【分析】一个圆柱的体积是与它等底等高的圆锥体积的3倍,原题没有注明“等底等高”或其它的条件,只说“圆柱的体积是圆锥体积的3倍”是错误的,据此判断.
9.【答案】错误
【解析】【解答】解:圆锥的体积等于与之等底等高的圆柱体积的/。 故答案为:错误。
【分析】圆锥的体积等于与之等底等高的圆柱体积的/
10.【答案】正确
【解析】【解答】解:根据圆锥的体积公式可知,圆锥的底面积扩大到原来的3倍,高不变,体积扩大到原来的3倍,原题说法正确. 故答案为:正确
【分析】圆锥的体积=底面积×高×/,所以圆锥体积扩大的倍数与底面积扩大的倍数相等.
11.【答案】错误
【解析】【解答】解:因为圆柱的体积是由它的底面积和高两个条件决定的,圆柱的高扩大3倍,它的底面积是否变化没有确定,所以它的体积也无法确定.
因此,圆柱体的高扩大3倍,体积就扩大3倍.此说法是错误的.
故答案为:错误.
【分析】根据圆柱的体积公式:v=sh,圆柱的体积是由它的底面积和高两个条件决定的,圆柱的高扩大3倍,它的底面积是否变化没有确定,所以它的体积也无法确定.
12.【答案】正确
【解析】【解答】解:长方体中除了相对的面完全相同,特殊情况下有2个相对的面是正方形,剩下的4个面是长方形,这四个面也是完全相同的,所以说长方体也有可能有两个相邻的面完全相同.原题说法正确. 故答案为:正确
【分析】特殊的长方体有两个正方形的面,另外的四个面是完全相同的长方形,这样的长方体就有两个相邻的面完全相同.
三、填空题
13.【答案】3;长;宽;高
【解析】【解答】在一个长方体的顶点上相交了3条棱,这三条棱的长度分别叫作长方体的长、宽、高. 故答案为:3;长;宽;高.
【分析】根据对长方体的认识可知,我们把相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高,习惯上,把水平方向的棱的长度作为长,把前后方向棱的长度作为宽,竖着的棱的长度作为高,据此解答.
14.【答案】12
【解析】【解答】解:圆锥的底面半径扩大2倍,它的底面积就扩大2×2=4倍,圆锥的高扩大3倍,那么圆锥的体积就扩大4×3=12倍.
答:它的体积扩大12倍.故答案为:12.
【分析】根据圆锥的体积公式:v=/sh,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此解答.
15.【答案】340
【解析】【解答】解:(60+40+)×2+30×4+20=100×2+120+20=340厘米;
答:绳子的长是340厘米.
故答案为:340.
【分析】由图可以观察,绳子的长度是2个长宽的长度和4个高的长度以及打结部分构成,由此即可解决问题.
16.【答案】2;8
【解析】【解答】如图:一个长方体最多可以有 2 个面是正方形,最多可以有 8 条棱长度相等。 / 【分析】有2个面是正方形的长方体,也是比较特殊的,最多可以有8条棱长度相等。
17.【答案】3.04
【解析】【解答】11.4×0.8×/ =9.12×/ =3.04(立方米) 故答案为:3.04
【分析】已知圆锥的底面积和高,求圆锥的体积,用公式:V=/Sh,据此列式解答.
18.【答案】48
【解析】【解答】解:2÷( /+ /),
=2÷ /,
=48(只);
答:共可制作48只水桶.
【分析】此题如果两张结合不会多产生下脚料话(一张铁皮制40个圆形底面后,还可以制底面加相同数量的侧面),可以用分数应用题的思路解答.把一张铁皮看做整体“1”,则一个圆形底面占1/60,一个侧面占1/40.然后根据题意列式解答即可.此题重点考查分数应用题与圆柱的展开图.
19.【答案】4.71;1.57
【解析】【解答】3.14÷(1-/)=4.71(立方分米),4.71×/=1.57(立方分米)
【分析】解答此题要明确等底等高的圆柱的体积等于圆锥体积的3倍,已知体积减少3.14立方分米,那么减少的部分是圆柱体积的(1-/),然后根据分数除法的意义求出圆柱的体积,再用圆柱的体积乘/就是圆锥的体积。
四、计算题
20.【答案】解:3.14×102×30×/ =3.14×100×10 =3140(cm2)
【解析】【分析】圆锥的体积=底面积×高×/,由此根据圆锥的体积公式计算即可.
五、解答题
21.【答案】解:以AB为轴,AD为底面半径时,底面积是最大的,所以AB为轴的表面积大.
【解析】【分析】圆柱的侧面积就是这个矩形的面积,所以圆柱的侧面积是不变的,那么底面积大的表面积就大,所以以AD为底面半径旋转后得到的圆柱的表面积最大.
22.【答案】解:由题意可知,所求花布的面积实际是求该圆柱5cm高的侧面积,
侧面展开图中,长方形的长即底面周长为:πd=6×3.14=18.84(cm)
长方形的宽即花布所围成圆柱的高为:5cm
则花布的面积为:S=Ch=18.84×5=94.2(cm2)
【解析】【分析】根据图意可知,要求花布的面积,就是求高5cm的圆柱的侧面积,先求出圆柱的底面周长,用公式:C=πd,然后用圆柱侧面积公式:S=Ch,据此列式解答.
六、综合题
23.【答案】(1)圆锥 (2)解:圆锥的体积= /×3.14×32×4.5
= /×3.14×9×4.5
=9.42×4.5
=42.39(立方厘米);
答:这个立体图形的体积是42.39立方厘米.
【解析】【解答】解:(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这个立体图形叫做圆锥.
【分析】(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这个立体图形叫做圆锥.(2)圆锥的体积= /×底面积×高,圆锥的底面半径和高已知,从而可以求出圆锥的体积.
七、应用题
24.【答案】解:3.14×(2.512÷3.14÷2)2 =3.14×0.42 =3.14×0.16 =0.5024(平方米), 答:这个油桶的底面积是0.5024平方米
【解析】【分析】把这个油桶放到在地面上滚动一圈的距离是2.512米,也就是油桶的底面周长是2.512米,根据圆的周长公式:c=2πr,求出底面半径,再根据圆的面积公式:s=πr2 , 把数据代入公式解答即可.此题主要考查圆的周长公式、面积公式在实际生活中的应用.
25.【答案】解:底面半径:48÷2÷12=2(厘米); 圆柱体积:3.14×22×12=150.72(立方厘米); 答:圆柱的体积是150.72立方厘米.
【解析】【分析】将一个圆柱切开后拼成一个近似的长方体,高没变,但拼成的长方体表面积比圆柱多了两个长方形的面积,这两个长方形的长都和圆柱的高相等,都是12厘米,宽都和圆柱的底面半径相等;已知表面积增加了48平方厘米,就可求出底面半径是多少厘米,进而再求出圆柱的体积即可.此题是求圆柱的体积,必须先知道底面半径和高,才可利用“V=Sh”来解答.
同课章节目录
- 一 比例
- 1、比例的意义与性质
- 2、正比例(一)
- 3、解比例
- 4、正比例(二)
- 5、正比例应用问题
- 6、反比例(一)
- 7、反比例(二)
- 8、反比例应用问题
- 二 比例尺
- 9、认识比例尺
- 10、比例尺的应用
- 11、方向与位置
- 四 圆柱与圆锥
- 16、圆柱与圆锥的认识
- 17、圆柱的表面积
- 18、圆柱的体积
- 19、圆锥的体积
- 五 整理与复习
- 20、整数与小数
- 21、数的整除
- 22、分数与百分数
- 23、加减运算
- 24、乘除运算
- 25、四则混合运算
- 26、代数式与方程
- 27、比与比例
- 28、应用问题
- 29、线与角
- 30、方向与位置
- 31、位置的确定
- 32、平面图形
- 33、图形的交换
- 34、立体图形
- 35、数据的整理
- 36、统计与可能性
- 总复习
