2018_2019高中数学第1章常用逻辑用语1.1.2充分条件和必要条件课件苏教版选修1_1(37张PPT)
文档属性
| 名称 | 2018_2019高中数学第1章常用逻辑用语1.1.2充分条件和必要条件课件苏教版选修1_1(37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-22 08:38:06 | ||
图片预览











文档简介
课件37张PPT。1.1.2 充分条件和必要条件第1章 §1.1 命题及其关系学习目标1.理解充分条件、必要条件的意义.
2.会判断、证明充要条件.
3.通过学习,明白对条件的判断应归结为判断命题的真假.问题导学达标检测题型探究内容索引问题导学知识点一 充分条件与必要条件的概念给出下列命题:
(1)若x>a2+b2,则x>2ab;
(2)若ab=0,则a=0.
思考1 你能判断这两个命题的真假吗?
答案 (1)真命题,
(2)假命题.
思考2 命题(1)中条件和结论有什么关系?命题(2)中呢?
答案 命题(1)中只要满足条件x>a2+b2,必有结论x>2ab;
命题(2)中满足条件ab=0,不一定有结论a=0,还可能b=0.梳理??充分必要充分必要思考1 命题“若整数a是6的倍数,则整数a是2和3的倍数”中的条件和结论有什么关系?它的逆命题成立吗?
答案 只要满足条件,必有结论成立,它的逆命题成立.
思考2 若设p:整数a是6的倍数,q:整数a是2和3的倍数,则p是q的什么条件?q是p的什么条件?
答案 因为p?q且q?p,所以p是q的充分条件也是必要条件;同理,q是p的充分条件,也是必要条件.知识点二 充要条件的概念梳理 一般地,如果p?q,且q?p,就记作 .此时,我们说,p是q的 ,简称充要条件.p?q充分必要条件知识点三 常见的四种条件1.从命题的真假判断充分条件、必要条件和充要条件
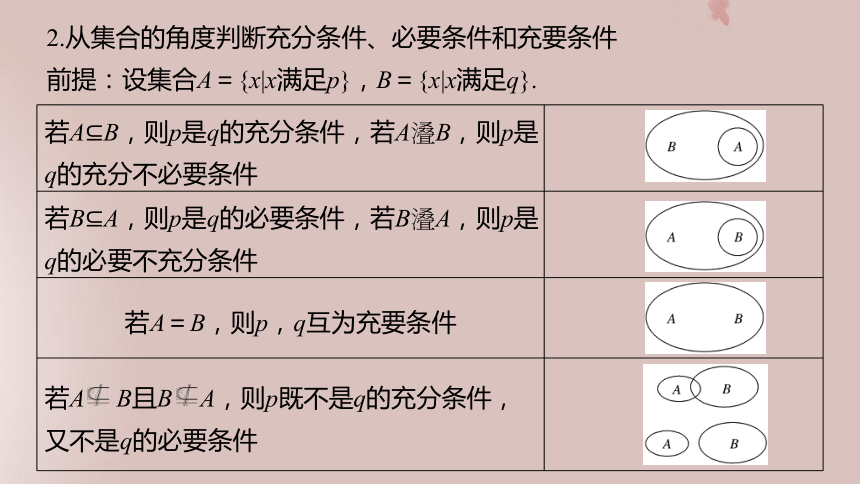
如果原命题为“若p则q”,逆命题为“若q则p”p?q,但q?pq?p,但p?qp?q,q?p,即p?qp?q,q?p2.从集合的角度判断充分条件、必要条件和充要条件
前提:设集合A={x|x满足p},B={x|x满足q}.1.若q是p的必要条件,则p是q的充分条件.( )
2.若p是q的充要条件,则命题p和q是两个相互等价的命题.( )
3.若q不是p的必要条件,则“p?q”成立.( )[思考辨析 判断正误]√√√题型探究例1 判断下列各题中,p是q的什么条件?类型一 充要条件的判断解答∴p是q的充分不必要条件.(2)p:(a-2)(a-3)=0,q:a=3;
解 由(a-2)(a-3)=0可以推出a=2或a=3,不一定有a=3;
由a=3可以推出(a-2)(a-3)=0,因此p是q的必要不充分条件.解答知a>b可以推出sin A>sin B,sin A>sin B可以推出a>b,
∴p是q的充要条件.(3)在△ABC中,p:a>b,q:sin A>sin B;(4)p:四边形的对角线相等,q:四边形是平行四边形.解答∴p是q的既不充分又不必要条件.反思与感悟 充分条件、必要条件的判断方法
(1)定义法:①确定谁是条件,谁是结论.
②尝试从条件推结论,若条件能推出结论,则条件为充分条件,否则就不是充分条件.
③尝试从结论推条件,若结论能推出条件,则条件为必要条件,否则就不是必要条件.
(2)命题判断法:
①如果命题:“若p则q”为真命题,那么p是q的充分条件,同时q是p的必要条件.
②如果命题:“若p则q”为假命题,那么p不是q的充分条件,同时q也不是p的必要条件.跟踪训练1 设x∈R,则“3-x≥0”是“|x-1|≤2”的___________条件.(填“充要”“充分不必要”“必要不充分”“既不充分又不必要”)
解析 ∵3-x≥0?x≤3,|x-1|≤2?-1≤x≤3,
故“3-x≥0”是“|x-1|≤2”的必要不充分条件.答案必要不充分解析类型二 充分条件、必要条件的应用例2 已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
解 p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的必要不充分条件,
所以q是p的充分不必要条件,
即{x|1-m≤x≤1+m}?{x|-2≤x≤10},解答又m>0,所以实数m的取值范围为{m|0<m≤3}.引申探究
1.若本例中“p是q的必要不充分条件”改为“p是q的充分不必要条件”,其他条件不变,求实数m的取值范围.
解 p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的充分不必要条件,
设p代表的集合为A,q代表的集合为B,所以A?B.解答解不等式组得m>9或m≥9,所以m≥9,
即实数m的取值范围是[9,+∞).2.本例中p,q不变,是否存在实数m使p是q的充要条件.
解 因为p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
若p是q的充要条件,则 m不存在.
故不存在实数m,使得p是q的充要条件.解答反思与感悟 (1)设集合A={x|x满足p},B={x|x满足q},则p?q可得A?B;q?p可得B?A;若p是q的充分不必要条件,则A?B.
(2)利用充分条件、必要条件求参数的取值范围的关键就是找出集合间的包含关系,要注意范围的临界值.跟踪训练2 已知M={x|(x-a)2<1},N={x|x2-5x-24<0},若M是N的充分条件,求a的取值范围.
解 由(x-a)2<1,得x2-2ax+(a-1)(a+1)<0,
∴a-1又由x2-5x-24<0,得-3∵M是N的充分条件,∴M?N,
∴ 解得-2≤a≤7.
即a的取值范围是[-2,7].解答例3 求证:一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.类型三 充要条件的证明证明证明 充分性:
∵ac<0,∴一元二次方程ax2+bx+c=0的判别式Δ=b2-4ac>0,
∴方程一定有两个不等实根.
设两实根为x1,x2,则x1x2= <0,∴方程的两根异号,
即方程ax2+bx+c=0有一正根和一负根.
必要性:
∵方程ax2+bx+c=0有一正根和一负根,
设两实根为x1,x2,则由根与系数的关系,得
x1x2= <0,且Δ=b2-4ac>0,即ac<0.
综上可知,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.引申探究
求证:关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.证明证明 必要性:
∵方程ax2+bx+c=0有一个根为1,
∴x=1满足方程ax2+bx+c=0,
∴a·12+b·1+c=0,即a+b+c=0,∴必要性成立.
充分性:
∵a+b+c=0,∴c=-a-b,代入方程ax2+bx+c=0中,可得ax2+bx-a-b=0,即(x-1)·(ax+a+b)=0,
故方程ax2+bx+c=0有一个根为1,∴充分性成立.
因此,关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.反思与感悟 (1)证明充要条件,一般是从充分性和必要性两方面进行,此时应特别注意充分性和必要性所推证的内容是什么.
(2)要分清命题中的条件和结论,防止充分性和必要性弄颠倒,由条件?结论是证充分性,由结论?条件是证必要性.跟踪训练3 已知数列{an}的前n项和为Sn=pn+q(p≠0且p≠1).求证:数列{an}为等比数列的充要条件为q=-1.证明证明 充分性:当q=-1时,a1=p-1;
当n≥2时,an=Sn-Sn-1=pn-1(p-1),
当n=1时也成立.
所以an=pn-1(p-1),n∈N*.∴数列{an}为等比数列.
必要性:当n=1时,a1=S1=p+q;
当n≥2时,an=Sn-Sn-1=pn-1(p-1).综上所述,q=-1是数列{an}为等比数列的充要条件.达标检测1.设M={1,2},N={a2},则“a=1”是“N?M”的____________条件. (填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
解析 当a=1时,N={1},此时N?M;
当N?M时,a2=1或a2=2,解得a=1或-1或 或- .
故“a=1”是“N?M”的充分不必要条件.充分不必要答案解析12345123452.“函数y=x2-2x-a没有零点”的充要条件是________.
解析 函数没有零点,即方程x2-2x-a=0无实根,所以有Δ=4+4a<0,解得a<-1.
反之,若a<-1,则Δ<0,方程x2-2x-a=0无实根,即函数没有零点.a<-1答案解析3.王昌龄的《从军行》中两句诗为“黄沙百战穿金甲,不破楼兰终不还”,其中后一句中“攻破楼兰”是“返回家乡”的_____条件.
解析 “攻破楼兰”是“返回家乡”的必要条件.12345答案解析必要答案解析4.若“x2>1”是“x解析 由x2>1,得x<-1或x>1.
又“x2>1”是“x则由“x1”,
但由“x2>1”推不出“x所以a≤-1,所以实数a的最大值为-1.12345-15.是否存在实数p,使得x2-x-2>0的一个充分条件是4x+p<0,若存在,求出p的取值范围,否则,说明理由.解答解 由x2-x-2>0,解得x>2或x<-1.
令A={x|x>2或x<-1}.∴当p≥4时,“4x+p<0”是“x2-x-2>0”的一个充分条件.123451.充分条件、必要条件的判断方法:
(1)定义法:直接利用定义进行判断.
(2)等价法:“p?q”表示p等价于q,要证p?q,只需证它的逆否命题非q?非p即可;同理要证p?q,只需证非q?非p即可.所以p?q,只需非q?非p.
(3)利用集合间的包含关系进行判断.
2.根据充分条件、必要条件求参数的取值范围时,主要根据充分条件、必要条件与集合间的关系,将问题转化为相应的两个集合之间的包含关系,然后建立关于参数的不等式(组)进行求解.
2.会判断、证明充要条件.
3.通过学习,明白对条件的判断应归结为判断命题的真假.问题导学达标检测题型探究内容索引问题导学知识点一 充分条件与必要条件的概念给出下列命题:
(1)若x>a2+b2,则x>2ab;
(2)若ab=0,则a=0.
思考1 你能判断这两个命题的真假吗?
答案 (1)真命题,
(2)假命题.
思考2 命题(1)中条件和结论有什么关系?命题(2)中呢?
答案 命题(1)中只要满足条件x>a2+b2,必有结论x>2ab;
命题(2)中满足条件ab=0,不一定有结论a=0,还可能b=0.梳理??充分必要充分必要思考1 命题“若整数a是6的倍数,则整数a是2和3的倍数”中的条件和结论有什么关系?它的逆命题成立吗?
答案 只要满足条件,必有结论成立,它的逆命题成立.
思考2 若设p:整数a是6的倍数,q:整数a是2和3的倍数,则p是q的什么条件?q是p的什么条件?
答案 因为p?q且q?p,所以p是q的充分条件也是必要条件;同理,q是p的充分条件,也是必要条件.知识点二 充要条件的概念梳理 一般地,如果p?q,且q?p,就记作 .此时,我们说,p是q的 ,简称充要条件.p?q充分必要条件知识点三 常见的四种条件1.从命题的真假判断充分条件、必要条件和充要条件
如果原命题为“若p则q”,逆命题为“若q则p”p?q,但q?pq?p,但p?qp?q,q?p,即p?qp?q,q?p2.从集合的角度判断充分条件、必要条件和充要条件
前提:设集合A={x|x满足p},B={x|x满足q}.1.若q是p的必要条件,则p是q的充分条件.( )
2.若p是q的充要条件,则命题p和q是两个相互等价的命题.( )
3.若q不是p的必要条件,则“p?q”成立.( )[思考辨析 判断正误]√√√题型探究例1 判断下列各题中,p是q的什么条件?类型一 充要条件的判断解答∴p是q的充分不必要条件.(2)p:(a-2)(a-3)=0,q:a=3;
解 由(a-2)(a-3)=0可以推出a=2或a=3,不一定有a=3;
由a=3可以推出(a-2)(a-3)=0,因此p是q的必要不充分条件.解答知a>b可以推出sin A>sin B,sin A>sin B可以推出a>b,
∴p是q的充要条件.(3)在△ABC中,p:a>b,q:sin A>sin B;(4)p:四边形的对角线相等,q:四边形是平行四边形.解答∴p是q的既不充分又不必要条件.反思与感悟 充分条件、必要条件的判断方法
(1)定义法:①确定谁是条件,谁是结论.
②尝试从条件推结论,若条件能推出结论,则条件为充分条件,否则就不是充分条件.
③尝试从结论推条件,若结论能推出条件,则条件为必要条件,否则就不是必要条件.
(2)命题判断法:
①如果命题:“若p则q”为真命题,那么p是q的充分条件,同时q是p的必要条件.
②如果命题:“若p则q”为假命题,那么p不是q的充分条件,同时q也不是p的必要条件.跟踪训练1 设x∈R,则“3-x≥0”是“|x-1|≤2”的___________条件.(填“充要”“充分不必要”“必要不充分”“既不充分又不必要”)
解析 ∵3-x≥0?x≤3,|x-1|≤2?-1≤x≤3,
故“3-x≥0”是“|x-1|≤2”的必要不充分条件.答案必要不充分解析类型二 充分条件、必要条件的应用例2 已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
解 p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的必要不充分条件,
所以q是p的充分不必要条件,
即{x|1-m≤x≤1+m}?{x|-2≤x≤10},解答又m>0,所以实数m的取值范围为{m|0<m≤3}.引申探究
1.若本例中“p是q的必要不充分条件”改为“p是q的充分不必要条件”,其他条件不变,求实数m的取值范围.
解 p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的充分不必要条件,
设p代表的集合为A,q代表的集合为B,所以A?B.解答解不等式组得m>9或m≥9,所以m≥9,
即实数m的取值范围是[9,+∞).2.本例中p,q不变,是否存在实数m使p是q的充要条件.
解 因为p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
若p是q的充要条件,则 m不存在.
故不存在实数m,使得p是q的充要条件.解答反思与感悟 (1)设集合A={x|x满足p},B={x|x满足q},则p?q可得A?B;q?p可得B?A;若p是q的充分不必要条件,则A?B.
(2)利用充分条件、必要条件求参数的取值范围的关键就是找出集合间的包含关系,要注意范围的临界值.跟踪训练2 已知M={x|(x-a)2<1},N={x|x2-5x-24<0},若M是N的充分条件,求a的取值范围.
解 由(x-a)2<1,得x2-2ax+(a-1)(a+1)<0,
∴a-1
∴ 解得-2≤a≤7.
即a的取值范围是[-2,7].解答例3 求证:一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.类型三 充要条件的证明证明证明 充分性:
∵ac<0,∴一元二次方程ax2+bx+c=0的判别式Δ=b2-4ac>0,
∴方程一定有两个不等实根.
设两实根为x1,x2,则x1x2= <0,∴方程的两根异号,
即方程ax2+bx+c=0有一正根和一负根.
必要性:
∵方程ax2+bx+c=0有一正根和一负根,
设两实根为x1,x2,则由根与系数的关系,得
x1x2= <0,且Δ=b2-4ac>0,即ac<0.
综上可知,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.引申探究
求证:关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.证明证明 必要性:
∵方程ax2+bx+c=0有一个根为1,
∴x=1满足方程ax2+bx+c=0,
∴a·12+b·1+c=0,即a+b+c=0,∴必要性成立.
充分性:
∵a+b+c=0,∴c=-a-b,代入方程ax2+bx+c=0中,可得ax2+bx-a-b=0,即(x-1)·(ax+a+b)=0,
故方程ax2+bx+c=0有一个根为1,∴充分性成立.
因此,关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.反思与感悟 (1)证明充要条件,一般是从充分性和必要性两方面进行,此时应特别注意充分性和必要性所推证的内容是什么.
(2)要分清命题中的条件和结论,防止充分性和必要性弄颠倒,由条件?结论是证充分性,由结论?条件是证必要性.跟踪训练3 已知数列{an}的前n项和为Sn=pn+q(p≠0且p≠1).求证:数列{an}为等比数列的充要条件为q=-1.证明证明 充分性:当q=-1时,a1=p-1;
当n≥2时,an=Sn-Sn-1=pn-1(p-1),
当n=1时也成立.
所以an=pn-1(p-1),n∈N*.∴数列{an}为等比数列.
必要性:当n=1时,a1=S1=p+q;
当n≥2时,an=Sn-Sn-1=pn-1(p-1).综上所述,q=-1是数列{an}为等比数列的充要条件.达标检测1.设M={1,2},N={a2},则“a=1”是“N?M”的____________条件. (填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
解析 当a=1时,N={1},此时N?M;
当N?M时,a2=1或a2=2,解得a=1或-1或 或- .
故“a=1”是“N?M”的充分不必要条件.充分不必要答案解析12345123452.“函数y=x2-2x-a没有零点”的充要条件是________.
解析 函数没有零点,即方程x2-2x-a=0无实根,所以有Δ=4+4a<0,解得a<-1.
反之,若a<-1,则Δ<0,方程x2-2x-a=0无实根,即函数没有零点.a<-1答案解析3.王昌龄的《从军行》中两句诗为“黄沙百战穿金甲,不破楼兰终不还”,其中后一句中“攻破楼兰”是“返回家乡”的_____条件.
解析 “攻破楼兰”是“返回家乡”的必要条件.12345答案解析必要答案解析4.若“x2>1”是“x
又“x2>1”是“x
但由“x2>1”推不出“x
令A={x|x>2或x<-1}.∴当p≥4时,“4x+p<0”是“x2-x-2>0”的一个充分条件.123451.充分条件、必要条件的判断方法:
(1)定义法:直接利用定义进行判断.
(2)等价法:“p?q”表示p等价于q,要证p?q,只需证它的逆否命题非q?非p即可;同理要证p?q,只需证非q?非p即可.所以p?q,只需非q?非p.
(3)利用集合间的包含关系进行判断.
2.根据充分条件、必要条件求参数的取值范围时,主要根据充分条件、必要条件与集合间的关系,将问题转化为相应的两个集合之间的包含关系,然后建立关于参数的不等式(组)进行求解.
