山东省泰安市2019中考专题复习——最值问题即最大值和最小值问题教案(含答案)
文档属性
| 名称 | 山东省泰安市2019中考专题复习——最值问题即最大值和最小值问题教案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 386.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-22 14:26:09 | ||
图片预览




文档简介
2019年中考专题复习-最值问题即最大值和最小值问题
最大值和最小值问题是中考的热点题型之一,泰安中考主要考察几何、一次函数和二次函数的最值问题。
一、几何问题:主要应用的原理是:利用“两点间线段最短”,利用轴对称求最短路线,利用垂线段最短的道理解决问题。
(一)利用“两点间线段最短”,找到动点,从而把问题解决。
1、(2018泰安12)如图1,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
(图1) (图2) (图3)
(二)利用轴对称求最短路线问题。利用轴对称确定动点的位置,利用有关几何知识求出答案。
此类问题的知识点是:七年级学习的“将军饮马”问题,例如:如图2,要在燃气管道l上修建一个泵站分别向A、B两镇供气. 泵站修在管道的什么地方,可使所用的输气管线最短?
2.(2016·福建龙岩)如图3,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
3、如图4所示,正方形的面积为12,是等边三角形,点在正方形内,在对角线上有一点,使的和最小,则这个最小值为( )
A. B. C.3 D.
(图4) (图5)
4、(2017泰安24).如图5,∠BAC=30°,M为AC上一点,AM=2,点P是AB上的一动点,PQ⊥AC,垂足为点Q,则PM+PQ的最小值为 .
(三)利用垂线段最短,将所求线段进行转化,进而求出答案。
5、如图6,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是____.
(图6) (图7)
6、如图7,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为 .
二、一次函数的最值问题
此类题目往往与方程组、不等式和分式方程应用进行结合,利用一次函数的增减性来解决问题。
7、(2018泰安20).(9分)文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
8、(2017泰安26).(8分)某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
9、(2016泰安26).(8分)某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
对应练习:
10、某水果店5月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.6月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店6月份购进这两种水果的数量与5月份都相同,将多支付货款300元,求该店5月份购进甲、乙两种水果分别是多少千克?
(2)若6月份将这两种水果进货总量减少到120千克,且甲种水果不超过乙种水果的3倍,则6月份该店需要支付这两种水果的货款最少应是多少元?
三、二次函数的最值问题:本部分最值问题解决关键是列出二次函数关系式,通过二次函数的性质解决相应的问题。
知识点:根据y=a(x-h)2+k,可知,a>0时,当x=h时,y最小值=k;a<0时,当x=h时,y最大值=k。
11、(2018泰安)如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(﹣4,0)、B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,﹣2),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
12、(2017泰安20).如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19cm2 B.16cm2 C.15cm2 D.12cm2
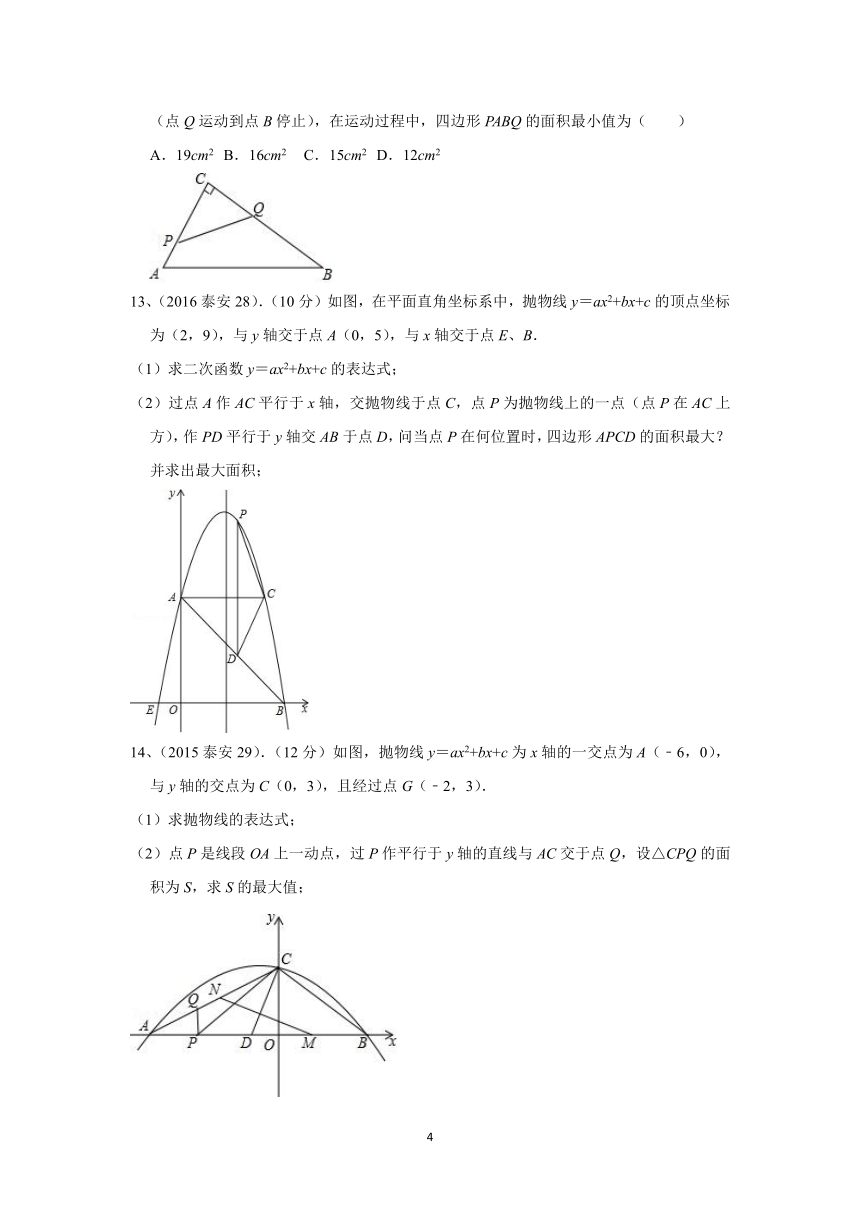
13、(2016泰安28).(10分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
14、(2015泰安29).(12分)如图,抛物线y=ax2+bx+c为x轴的一交点为A(﹣6,0),与y轴的交点为C(0,3),且经过点G(﹣2,3).
(1)求抛物线的表达式;
(2)点P是线段OA上一动点,过P作平行于y轴的直线与AC交于点Q,设△CPQ的面积为S,求S的最大值;
15、(2014泰安29).(11分)二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
练习题:
16、如图,在平面直角坐标系中,二次函数y=ax2+bx﹣3交x轴于点A(﹣3,0)、B(1,0),在y轴上有一点E(0,1),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴下方的一个动点,求△ADE面积的最大值;
17、如图,已知二次函数y=x2﹣3x﹣4的图象交x轴于A、B两点.
(1)若点P在线段AB上运动,作PQ⊥x轴,交抛物线于点Q,求PQ的最大值;
(2)已知点D(5,6)在抛物线上,若点M在线段AD上运动,作MN⊥x轴,交抛物线于点N,求MN的最大值;
参考答案
1、解:∵PA⊥PB,∴∠APB=90°,∵AO=BO,∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,
过点M作MQ⊥x轴于点Q,
则OQ=3、MQ=4,∴OM=5,
又∵MP′=2,∴OP′=3,∴AB=2OP′=6,故选:C.
(1题图) (2题图)
2、解:如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8,
∴AB=BC=4,AB?CE′=8,∴CE′=2,
在Rt△BCE′中,BE′==2,
∵BE=EA=2,∴E与E′重合,
∵四边形ABCD是菱形,∴BD垂直平分AC,∴A、C关于BD对称,
∴当P与P′重合时,P′A+P′E的值最小,最小值为CE的长=2,
故答案为2.
3、解:连接BD,与AC交于点F.
∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为12,∴AB=2.
又∵△ABE是等边三角形,∴BE=AB=2.故所求最小值为2.
(3题图) (4题图) (5题图)
4、解:作点M关于AB的对称点N,过N作NQ⊥AC于Q交AB于P,
则NQ的长即为PM+PQ的最小值,
连接MN交AB于D,则MD⊥AB,DM=DN,
∵∠NPB=∠APQ,∴∠N=∠BAC=30°,
∵∠BAC=30°,AM=2,∴MD=AM=1,∴MN=2,
∴NQ=MN?cos∠N=2×=,故答案为:.
5、解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.
∵AD是∠BAC的平分线,
∴M′H=M′N′,
∴BH是点B到直线AC的最短距离(垂线段最短),
∵AB=4,∠BAC=45°,
∴BH=AB?sin45°=4×=2.
∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=2.
故答案为:2.
6、
7、解:(1)设乙种图书售价每本x元,则甲种图书售价为每本1.4x元
由题意得: 解得:x=20
经检验,x=20是原方程的解∴甲种图书售价为每本1.4×20=28元
答:甲种图书售价每本28元,乙种图书售价每本20元
(2)设甲种图书进货a本,总利润W元,则
W=(28﹣20﹣3)a+(20﹣14﹣2)(1200﹣a)=a+4800
∵20a+14×(1200﹣a)≤20000
解得a≤
∵w随a的增大而增大∴当a最大时w最大∴当a=533本时,w最大
此时,乙种图书进货本数为1200﹣533=667(本)
答:甲种图书进货533本,乙种图书进货667本时利润最大.
8、解:(1)设小樱桃的进价为每千克x元,大樱桃的进价为每千克y元,根据题意可得:
,解得:,
小樱桃的进价为每千克10元,大樱桃的进价为每千克30元,
200×[(40﹣30)+(16﹣10)]=3200(元),
∴销售完后,该水果商共赚了3200元;
(2)设大樱桃的售价为a元/千克,
(1﹣20%)×200×16+200a﹣8000≥3200×90%,解得:a≥41.6,
答:大樱桃的售价最少应为41.6元/千克.
9、解:(1)设直拍球拍每副x元,横拍球每副y元,由题意得,
,
解得,,
答:直拍球拍每副220元,横拍球每副260元;
(2)设购买直拍球拍m副,则购买横拍球(40﹣m)副,
由题意得,m≤3(40﹣m),解得,m≤30,
设买40副球拍所需的费用为w,
则w=(220+20)m+(260+20)(40﹣m)=﹣40m+11200,
∵﹣40<0,
∴w随m的增大而减小,
∴当m=30时,w取最小值,最小值为﹣40×30+11200=10000(元).
答:购买直拍球拍30副,则购买横拍球10副时,费用最少.
10、解:(1)设该店5月份购进甲种水果x千克,购进乙种水果y千克,
根据题意得:,
解得:.
答:该店5月份购进甲种水果100千克,购进乙种水果50千克.
(2)设购进甲种水果a千克,需要支付的货款为w元,则购进乙种水果(120﹣a)千克,
根据题意得:w=10a+20(120﹣a)=﹣10a+2400.
∵甲种水果不超过乙种水果的3倍,
∴a≤3(120﹣a),
解得:a≤90.
∵k=﹣10<0,
∴w随a值的增大而减小,
∴当a=90时,w取最小值,最小值﹣10×90+2400=1500.
∴月份该店需要支付这两种水果的货款最少应是1500元.
11、解:(1)∵二次函数y=ax2+bx+c经过点A(﹣4,0)、B(2,0),C(0,6),
∴,解得,,
所以二次函数的解析式为:y=,
(2)由A(﹣4,0),E(0,﹣2),可求AE所在直线解析式为y=,
过点D作DG⊥x轴于G,交AE于点F,交x轴于点G,过点E作EH⊥DF,垂足为H,如图
设D(m,),则点F(m,),
∴DF=﹣()=,
∴S△ADE=S△ADF+S△EDF=×DF×AG+DF×EH
=×DF×(AG+EH)
=×4×DF
=2×()
=,
∴当m=时,△ADE的面积取得最大值为.
12、解:(方法一)在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,
∴AC==6cm.
设运动时间为t(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,
∴S四边形PABQ=S△ABC﹣S△CPQ=AC?BC﹣PC?CQ=×6×8﹣(6﹣t)×2t=t2﹣6t+24=(t﹣3)2+15.
∵1>0,
∴当t=3时,四边形PABQ的面积取最小值,最小值为15.
(方法二)∵S四边形PABQ+S△CPQ=S△ABC,
∴当△CPQ的面积最大时,四边形PABQ的面积最小.
在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,∴AC==6cm.
设运动时间为t(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,
∴S△CPQ=PC?CQ=×(6﹣t)×2t=﹣t2+6t=﹣(t﹣3)2+9.
∵﹣1<0,
∴当t=3时,△CPQ的面积取最大值,最大值为9,
∴四边形PABQ的面积最小值为×6×8﹣9=15.
故选:C.
13、解:(1)设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),∴4a+9=5,∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5,
(2)当y=0时,﹣x2+4x+5=0,∴x1=﹣1,x2=5,∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),∴m=﹣1,n=5,∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,∵AC=4,
∴S四边形APCD=×AC×PD=2(﹣x2+5x)=﹣2x2+10x,
∴当x=﹣=时,
∴即:点P(,)时,S四边形APCD最大=,
14、解:(1)把A、C、G三点坐标代入抛物线解析式可得,解得,
∴抛物线的表达式为y=﹣x2﹣x+3;
(2)∵C(0,3),
∴可设直线AC解析式为y=kx+3,把A点坐标代入可得0=﹣6k+3,解得k=,
∴直线AC解析式为y=x+3,
设P点坐标为(x,0)(x<0),则Q点坐标为(x,x+3),∴PQ=x+3,PO=﹣x,
∴S=PQ?PO=(x+3)(﹣x)=﹣x2﹣x=﹣(x+3)2+,
∴△CPQ的面积S的最大值为;
15、解:(1)由直线y=﹣x+1可知A(0,1),B(﹣3,),又点(﹣1,4)经过二次函数,
根据题意得:,解得:,
则二次函数的解析式是:y=﹣﹣x+1;
(2)设N(x,﹣x2﹣x+1),则M(x,﹣x+1),P(x,0).
∴MN=PN﹣PM=﹣x2﹣x+1﹣(﹣x+1)
=﹣x2﹣x=﹣(x+)2+,
则当x=﹣时,MN的最大值为;
16、解:(1)∵二次函数y=ax2+bx﹣3经过点A(﹣3,0)、B(1,0),
∴,解得:,
∴二次函数解析式为y=x2+2x﹣3;
(2)设直线AE的解析式为y=kx+b,
∵过点A(﹣3,0),E(0,1),
∴,解得:,∴直线AE解析式为y=x+1,
如图,过点D作DG⊥x轴于点G,延长DG交AE于点F,
设D(m,m2+2m﹣3),则F(m,m+1),
∴DF=﹣m2﹣2m+3+m+1=﹣m2﹣m+4,
∴S△ADE=S△ADF+S△DEF=×DF×AG+DF×OG
=×DF×(AG+OG)=×3×DF
=(﹣m2﹣m+4)=﹣m2﹣m+6
=﹣(m+)2+,
∴当m=﹣时,△ADE的面积取得最大值为.
17、解:(1)当Q为抛物线的顶点时,PQ取得最大值.
∵y=x2﹣3x﹣4=(x﹣)2﹣,∴点Q坐标为(,﹣),
∴PQ的最大值为;
(2)∵D(5,6),A(﹣1,0),设直线AD的解析式为:y=kx+b,则
,解得.∴直线AD的解析式为:y=x+1;
设M(x,x+1),则N(x,x2﹣3x﹣4),
∴MN=x+1﹣(x2﹣3x﹣4)=﹣x2+4x+5=﹣(x﹣2)2+9,
∴当x=2时,MN的最大值为9;
A
D
E
P
B
C
最大值和最小值问题是中考的热点题型之一,泰安中考主要考察几何、一次函数和二次函数的最值问题。
一、几何问题:主要应用的原理是:利用“两点间线段最短”,利用轴对称求最短路线,利用垂线段最短的道理解决问题。
(一)利用“两点间线段最短”,找到动点,从而把问题解决。
1、(2018泰安12)如图1,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
(图1) (图2) (图3)
(二)利用轴对称求最短路线问题。利用轴对称确定动点的位置,利用有关几何知识求出答案。
此类问题的知识点是:七年级学习的“将军饮马”问题,例如:如图2,要在燃气管道l上修建一个泵站分别向A、B两镇供气. 泵站修在管道的什么地方,可使所用的输气管线最短?
2.(2016·福建龙岩)如图3,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
3、如图4所示,正方形的面积为12,是等边三角形,点在正方形内,在对角线上有一点,使的和最小,则这个最小值为( )
A. B. C.3 D.
(图4) (图5)
4、(2017泰安24).如图5,∠BAC=30°,M为AC上一点,AM=2,点P是AB上的一动点,PQ⊥AC,垂足为点Q,则PM+PQ的最小值为 .
(三)利用垂线段最短,将所求线段进行转化,进而求出答案。
5、如图6,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是____.
(图6) (图7)
6、如图7,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为 .
二、一次函数的最值问题
此类题目往往与方程组、不等式和分式方程应用进行结合,利用一次函数的增减性来解决问题。
7、(2018泰安20).(9分)文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
8、(2017泰安26).(8分)某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
9、(2016泰安26).(8分)某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
对应练习:
10、某水果店5月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.6月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店6月份购进这两种水果的数量与5月份都相同,将多支付货款300元,求该店5月份购进甲、乙两种水果分别是多少千克?
(2)若6月份将这两种水果进货总量减少到120千克,且甲种水果不超过乙种水果的3倍,则6月份该店需要支付这两种水果的货款最少应是多少元?
三、二次函数的最值问题:本部分最值问题解决关键是列出二次函数关系式,通过二次函数的性质解决相应的问题。
知识点:根据y=a(x-h)2+k,可知,a>0时,当x=h时,y最小值=k;a<0时,当x=h时,y最大值=k。
11、(2018泰安)如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(﹣4,0)、B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,﹣2),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
12、(2017泰安20).如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19cm2 B.16cm2 C.15cm2 D.12cm2
13、(2016泰安28).(10分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
14、(2015泰安29).(12分)如图,抛物线y=ax2+bx+c为x轴的一交点为A(﹣6,0),与y轴的交点为C(0,3),且经过点G(﹣2,3).
(1)求抛物线的表达式;
(2)点P是线段OA上一动点,过P作平行于y轴的直线与AC交于点Q,设△CPQ的面积为S,求S的最大值;
15、(2014泰安29).(11分)二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
练习题:
16、如图,在平面直角坐标系中,二次函数y=ax2+bx﹣3交x轴于点A(﹣3,0)、B(1,0),在y轴上有一点E(0,1),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴下方的一个动点,求△ADE面积的最大值;
17、如图,已知二次函数y=x2﹣3x﹣4的图象交x轴于A、B两点.
(1)若点P在线段AB上运动,作PQ⊥x轴,交抛物线于点Q,求PQ的最大值;
(2)已知点D(5,6)在抛物线上,若点M在线段AD上运动,作MN⊥x轴,交抛物线于点N,求MN的最大值;
参考答案
1、解:∵PA⊥PB,∴∠APB=90°,∵AO=BO,∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,
过点M作MQ⊥x轴于点Q,
则OQ=3、MQ=4,∴OM=5,
又∵MP′=2,∴OP′=3,∴AB=2OP′=6,故选:C.
(1题图) (2题图)
2、解:如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8,
∴AB=BC=4,AB?CE′=8,∴CE′=2,
在Rt△BCE′中,BE′==2,
∵BE=EA=2,∴E与E′重合,
∵四边形ABCD是菱形,∴BD垂直平分AC,∴A、C关于BD对称,
∴当P与P′重合时,P′A+P′E的值最小,最小值为CE的长=2,
故答案为2.
3、解:连接BD,与AC交于点F.
∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为12,∴AB=2.
又∵△ABE是等边三角形,∴BE=AB=2.故所求最小值为2.
(3题图) (4题图) (5题图)
4、解:作点M关于AB的对称点N,过N作NQ⊥AC于Q交AB于P,
则NQ的长即为PM+PQ的最小值,
连接MN交AB于D,则MD⊥AB,DM=DN,
∵∠NPB=∠APQ,∴∠N=∠BAC=30°,
∵∠BAC=30°,AM=2,∴MD=AM=1,∴MN=2,
∴NQ=MN?cos∠N=2×=,故答案为:.
5、解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.
∵AD是∠BAC的平分线,
∴M′H=M′N′,
∴BH是点B到直线AC的最短距离(垂线段最短),
∵AB=4,∠BAC=45°,
∴BH=AB?sin45°=4×=2.
∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=2.
故答案为:2.
6、
7、解:(1)设乙种图书售价每本x元,则甲种图书售价为每本1.4x元
由题意得: 解得:x=20
经检验,x=20是原方程的解∴甲种图书售价为每本1.4×20=28元
答:甲种图书售价每本28元,乙种图书售价每本20元
(2)设甲种图书进货a本,总利润W元,则
W=(28﹣20﹣3)a+(20﹣14﹣2)(1200﹣a)=a+4800
∵20a+14×(1200﹣a)≤20000
解得a≤
∵w随a的增大而增大∴当a最大时w最大∴当a=533本时,w最大
此时,乙种图书进货本数为1200﹣533=667(本)
答:甲种图书进货533本,乙种图书进货667本时利润最大.
8、解:(1)设小樱桃的进价为每千克x元,大樱桃的进价为每千克y元,根据题意可得:
,解得:,
小樱桃的进价为每千克10元,大樱桃的进价为每千克30元,
200×[(40﹣30)+(16﹣10)]=3200(元),
∴销售完后,该水果商共赚了3200元;
(2)设大樱桃的售价为a元/千克,
(1﹣20%)×200×16+200a﹣8000≥3200×90%,解得:a≥41.6,
答:大樱桃的售价最少应为41.6元/千克.
9、解:(1)设直拍球拍每副x元,横拍球每副y元,由题意得,
,
解得,,
答:直拍球拍每副220元,横拍球每副260元;
(2)设购买直拍球拍m副,则购买横拍球(40﹣m)副,
由题意得,m≤3(40﹣m),解得,m≤30,
设买40副球拍所需的费用为w,
则w=(220+20)m+(260+20)(40﹣m)=﹣40m+11200,
∵﹣40<0,
∴w随m的增大而减小,
∴当m=30时,w取最小值,最小值为﹣40×30+11200=10000(元).
答:购买直拍球拍30副,则购买横拍球10副时,费用最少.
10、解:(1)设该店5月份购进甲种水果x千克,购进乙种水果y千克,
根据题意得:,
解得:.
答:该店5月份购进甲种水果100千克,购进乙种水果50千克.
(2)设购进甲种水果a千克,需要支付的货款为w元,则购进乙种水果(120﹣a)千克,
根据题意得:w=10a+20(120﹣a)=﹣10a+2400.
∵甲种水果不超过乙种水果的3倍,
∴a≤3(120﹣a),
解得:a≤90.
∵k=﹣10<0,
∴w随a值的增大而减小,
∴当a=90时,w取最小值,最小值﹣10×90+2400=1500.
∴月份该店需要支付这两种水果的货款最少应是1500元.
11、解:(1)∵二次函数y=ax2+bx+c经过点A(﹣4,0)、B(2,0),C(0,6),
∴,解得,,
所以二次函数的解析式为:y=,
(2)由A(﹣4,0),E(0,﹣2),可求AE所在直线解析式为y=,
过点D作DG⊥x轴于G,交AE于点F,交x轴于点G,过点E作EH⊥DF,垂足为H,如图
设D(m,),则点F(m,),
∴DF=﹣()=,
∴S△ADE=S△ADF+S△EDF=×DF×AG+DF×EH
=×DF×(AG+EH)
=×4×DF
=2×()
=,
∴当m=时,△ADE的面积取得最大值为.
12、解:(方法一)在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,
∴AC==6cm.
设运动时间为t(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,
∴S四边形PABQ=S△ABC﹣S△CPQ=AC?BC﹣PC?CQ=×6×8﹣(6﹣t)×2t=t2﹣6t+24=(t﹣3)2+15.
∵1>0,
∴当t=3时,四边形PABQ的面积取最小值,最小值为15.
(方法二)∵S四边形PABQ+S△CPQ=S△ABC,
∴当△CPQ的面积最大时,四边形PABQ的面积最小.
在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,∴AC==6cm.
设运动时间为t(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,
∴S△CPQ=PC?CQ=×(6﹣t)×2t=﹣t2+6t=﹣(t﹣3)2+9.
∵﹣1<0,
∴当t=3时,△CPQ的面积取最大值,最大值为9,
∴四边形PABQ的面积最小值为×6×8﹣9=15.
故选:C.
13、解:(1)设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),∴4a+9=5,∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5,
(2)当y=0时,﹣x2+4x+5=0,∴x1=﹣1,x2=5,∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),∴m=﹣1,n=5,∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,∵AC=4,
∴S四边形APCD=×AC×PD=2(﹣x2+5x)=﹣2x2+10x,
∴当x=﹣=时,
∴即:点P(,)时,S四边形APCD最大=,
14、解:(1)把A、C、G三点坐标代入抛物线解析式可得,解得,
∴抛物线的表达式为y=﹣x2﹣x+3;
(2)∵C(0,3),
∴可设直线AC解析式为y=kx+3,把A点坐标代入可得0=﹣6k+3,解得k=,
∴直线AC解析式为y=x+3,
设P点坐标为(x,0)(x<0),则Q点坐标为(x,x+3),∴PQ=x+3,PO=﹣x,
∴S=PQ?PO=(x+3)(﹣x)=﹣x2﹣x=﹣(x+3)2+,
∴△CPQ的面积S的最大值为;
15、解:(1)由直线y=﹣x+1可知A(0,1),B(﹣3,),又点(﹣1,4)经过二次函数,
根据题意得:,解得:,
则二次函数的解析式是:y=﹣﹣x+1;
(2)设N(x,﹣x2﹣x+1),则M(x,﹣x+1),P(x,0).
∴MN=PN﹣PM=﹣x2﹣x+1﹣(﹣x+1)
=﹣x2﹣x=﹣(x+)2+,
则当x=﹣时,MN的最大值为;
16、解:(1)∵二次函数y=ax2+bx﹣3经过点A(﹣3,0)、B(1,0),
∴,解得:,
∴二次函数解析式为y=x2+2x﹣3;
(2)设直线AE的解析式为y=kx+b,
∵过点A(﹣3,0),E(0,1),
∴,解得:,∴直线AE解析式为y=x+1,
如图,过点D作DG⊥x轴于点G,延长DG交AE于点F,
设D(m,m2+2m﹣3),则F(m,m+1),
∴DF=﹣m2﹣2m+3+m+1=﹣m2﹣m+4,
∴S△ADE=S△ADF+S△DEF=×DF×AG+DF×OG
=×DF×(AG+OG)=×3×DF
=(﹣m2﹣m+4)=﹣m2﹣m+6
=﹣(m+)2+,
∴当m=﹣时,△ADE的面积取得最大值为.
17、解:(1)当Q为抛物线的顶点时,PQ取得最大值.
∵y=x2﹣3x﹣4=(x﹣)2﹣,∴点Q坐标为(,﹣),
∴PQ的最大值为;
(2)∵D(5,6),A(﹣1,0),设直线AD的解析式为:y=kx+b,则
,解得.∴直线AD的解析式为:y=x+1;
设M(x,x+1),则N(x,x2﹣3x﹣4),
∴MN=x+1﹣(x2﹣3x﹣4)=﹣x2+4x+5=﹣(x﹣2)2+9,
∴当x=2时,MN的最大值为9;
A
D
E
P
B
C
同课章节目录
