2018_2019学年高中数学第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件新人教A版选修1_1(32张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件新人教A版选修1_1(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-23 00:00:00 | ||
图片预览











文档简介
课件32张PPT。§2.2 双曲线
§2.2.1 双曲线及其标准方程
[课标解读]
1.掌握双曲线的定义、几何图形和标准方程.(重点、易混点)
2.会利用双曲线的定义和标准方程解决一些简单的问题.(重点)
1.双曲线的定义
(1)定义:平面内与两个定点F1,F2的距离的差的_______等于常数(_____|F1F2|)的点的轨迹.
(2)符号表示:||MF1|-|MF2||=2a(常数) (0<2a<|F1F2|).
(3)焦点:两个_____________.
(4)焦距:___________的距离,表示为|F1F2|.
教材知识梳理绝对值小于定点F1,F2两焦点间2.双曲线的标准方程
(-c,0),(c,0)(0,-c),(0,c)a2+b2知识点一 双曲线定义
探究1:通过下列问题的处理,体会双曲线的形成过程.
(1)若把椭圆定义中的与两定点的“距离之和”改成“距离之差的绝对值”,这时轨迹又是什么曲线?
提示 双曲线.
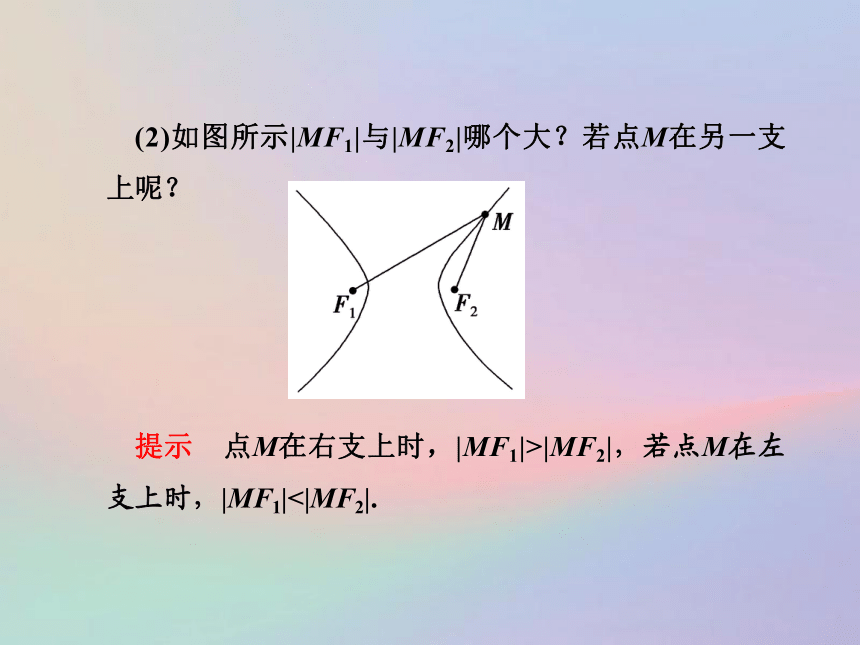
核心要点探究(2)如图所示|MF1|与|MF2|哪个大?若点M在另一支上呢?
提示 点M在右支上时,|MF1|>|MF2|,若点M在左支上时,|MF1|<|MF2|.
探究2:双曲线定义如同椭圆一样,规定了参数与两定点之间距离的大小关系,探究下面问题,体会此规定的原因.
(1)若0提示 双曲线.
(2)若a=c,动点M的轨迹又是什么?
提示 两条射线.
(3)若a=0,动点M的轨迹又是什么?
提示 线段F1F2的中垂线.
(4)若a>c,动点M的轨迹又是什么?
提示 不存在.
知识点二 双曲线的标准方程
探究1:观察双曲线的标准方程,探究下列问题,明确双曲线标准方程的特点.
(1)双曲线的标准方程左右两侧各具有怎样的结构特征?
提示 双曲线的标准方程左端为两平方项的差,右端为常数1.
(2)类比椭圆的标准方程,双曲线的标准方程可以根据x2与y2分母的大小来判断双曲线焦点的位置吗?
提示 双曲线焦点的位置不是由标准方程中x2与y2的分母大小判断,而是根据x2与y2项的系数的正负区分.
(3)双曲线方程中a与b,c的关系是怎样的?
提示 a与b的大小关系不确定,a探究2:通过对下列问题的探究,明确确定双曲线标准方程的关键.
(1)利用待定系数法求双曲线标准方程的关键是什么?
提示 确定参数a,b的值.
(2)求双曲线的标准方程时,设出双曲线方程的关键是什么?
提示 关键是先确定焦点的位置,若双曲线的焦点位置不能确定,要分别写出焦点在x轴、y轴上的双曲线的标准方程,不能遗漏.
题型一 双曲线定义的应用例1【答案】 B◎变式训练解析 ∵a=3,b=4,∴c=5,
又|PF2|=|F1F2|,
∴|PF1|-|PF2|=|PF1|-|F1F2|=2a,
∴|PF1|-10=6,∴|PF1|=16,|PF2|=10,
答案 C题型二 求双曲线的标准方程例22.求双曲线标准方程的两个关注点
(1)定位:“定位”是指确定与坐标系的相对位置,在“标准方程”的前提下,确定焦点位于哪条坐标轴上,以判断方程的形式.
(2)定量:“定量”是指确定a2,b2的具体数值,常根据条件列方程求解.
◎变式训练题型三 由双曲线标准方程求参数例3(3)已知方程所代表的曲线,求参数的取值范围时,应先将方程转化为所对应曲线的标准方程的形式,再根据方程中参数取值的要求,建立不等式(组)求解参数的取值范围.
3.已知双曲线8kx2-ky2=8的一个焦点为(0,3),求k的值.
◎对点训练 已知定点A(-3,0)和定圆C:(x-3)2+y2=16,动圆和圆C相外切,并且过定点A,求动圆圆心M的轨迹方程.
易错误区(五) 双曲线的定义理解中的误区典例典题示例[易错防范]
1.求解中易把动点的轨迹看成双曲线,忽视了双曲线定义中“距离的差的绝对值是常数”这一条件,动点轨迹实际上是双曲线的一支.
2.在求解与双曲线有关的轨迹问题时,准确理解双曲线的定义,才能保证解题的正确性.当||PF1|-|PF2||=2a<|F1F2|(a>0),即|PF1|-|PF2|=±2a(0<2a<|F1F2|)时,P点的轨迹是双曲线,其中取正号时为双曲线的右支,取负号时为双曲线的左支.
求与⊙C1:x2+(y-1)2=1和⊙C2:x2+(y+1)2=4都外切的动圆圆心M的轨迹方程.
典题试解
§2.2.1 双曲线及其标准方程
[课标解读]
1.掌握双曲线的定义、几何图形和标准方程.(重点、易混点)
2.会利用双曲线的定义和标准方程解决一些简单的问题.(重点)
1.双曲线的定义
(1)定义:平面内与两个定点F1,F2的距离的差的_______等于常数(_____|F1F2|)的点的轨迹.
(2)符号表示:||MF1|-|MF2||=2a(常数) (0<2a<|F1F2|).
(3)焦点:两个_____________.
(4)焦距:___________的距离,表示为|F1F2|.
教材知识梳理绝对值小于定点F1,F2两焦点间2.双曲线的标准方程
(-c,0),(c,0)(0,-c),(0,c)a2+b2知识点一 双曲线定义
探究1:通过下列问题的处理,体会双曲线的形成过程.
(1)若把椭圆定义中的与两定点的“距离之和”改成“距离之差的绝对值”,这时轨迹又是什么曲线?
提示 双曲线.
核心要点探究(2)如图所示|MF1|与|MF2|哪个大?若点M在另一支上呢?
提示 点M在右支上时,|MF1|>|MF2|,若点M在左支上时,|MF1|<|MF2|.
探究2:双曲线定义如同椭圆一样,规定了参数与两定点之间距离的大小关系,探究下面问题,体会此规定的原因.
(1)若0
(2)若a=c,动点M的轨迹又是什么?
提示 两条射线.
(3)若a=0,动点M的轨迹又是什么?
提示 线段F1F2的中垂线.
(4)若a>c,动点M的轨迹又是什么?
提示 不存在.
知识点二 双曲线的标准方程
探究1:观察双曲线的标准方程,探究下列问题,明确双曲线标准方程的特点.
(1)双曲线的标准方程左右两侧各具有怎样的结构特征?
提示 双曲线的标准方程左端为两平方项的差,右端为常数1.
(2)类比椭圆的标准方程,双曲线的标准方程可以根据x2与y2分母的大小来判断双曲线焦点的位置吗?
提示 双曲线焦点的位置不是由标准方程中x2与y2的分母大小判断,而是根据x2与y2项的系数的正负区分.
(3)双曲线方程中a与b,c的关系是怎样的?
提示 a与b的大小关系不确定,a
(1)利用待定系数法求双曲线标准方程的关键是什么?
提示 确定参数a,b的值.
(2)求双曲线的标准方程时,设出双曲线方程的关键是什么?
提示 关键是先确定焦点的位置,若双曲线的焦点位置不能确定,要分别写出焦点在x轴、y轴上的双曲线的标准方程,不能遗漏.
题型一 双曲线定义的应用例1【答案】 B◎变式训练解析 ∵a=3,b=4,∴c=5,
又|PF2|=|F1F2|,
∴|PF1|-|PF2|=|PF1|-|F1F2|=2a,
∴|PF1|-10=6,∴|PF1|=16,|PF2|=10,
答案 C题型二 求双曲线的标准方程例22.求双曲线标准方程的两个关注点
(1)定位:“定位”是指确定与坐标系的相对位置,在“标准方程”的前提下,确定焦点位于哪条坐标轴上,以判断方程的形式.
(2)定量:“定量”是指确定a2,b2的具体数值,常根据条件列方程求解.
◎变式训练题型三 由双曲线标准方程求参数例3(3)已知方程所代表的曲线,求参数的取值范围时,应先将方程转化为所对应曲线的标准方程的形式,再根据方程中参数取值的要求,建立不等式(组)求解参数的取值范围.
3.已知双曲线8kx2-ky2=8的一个焦点为(0,3),求k的值.
◎对点训练 已知定点A(-3,0)和定圆C:(x-3)2+y2=16,动圆和圆C相外切,并且过定点A,求动圆圆心M的轨迹方程.
易错误区(五) 双曲线的定义理解中的误区典例典题示例[易错防范]
1.求解中易把动点的轨迹看成双曲线,忽视了双曲线定义中“距离的差的绝对值是常数”这一条件,动点轨迹实际上是双曲线的一支.
2.在求解与双曲线有关的轨迹问题时,准确理解双曲线的定义,才能保证解题的正确性.当||PF1|-|PF2||=2a<|F1F2|(a>0),即|PF1|-|PF2|=±2a(0<2a<|F1F2|)时,P点的轨迹是双曲线,其中取正号时为双曲线的右支,取负号时为双曲线的左支.
求与⊙C1:x2+(y-1)2=1和⊙C2:x2+(y+1)2=4都外切的动圆圆心M的轨迹方程.
典题试解
