高中数学第三章数系的扩充与复数3.1.3复数的几何意义课件 新人教B版选修2_2(15张PPT)
文档属性
| 名称 | 高中数学第三章数系的扩充与复数3.1.3复数的几何意义课件 新人教B版选修2_2(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 977.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-23 00:00:00 | ||
图片预览





文档简介
课件15张PPT。知识回顾1、复数的概念:形如______________的数叫做复数,a,b分别叫做它的_____________。为纯虚数
实数 非纯虚数
2、复数Z1=a1+b1i与Z2=a2+b2i 相等的充要条件是_____________。a1=a2,b1=b2a+bi (a,b∈R)实部和虚部a=0,b≠0b=0a ≠ 0,b≠0复数的几何意义知识回顾1、复数的概念:形如______________的数叫做复数,a,b分别叫做它的_____________。为纯虚数
实数 非纯虚数
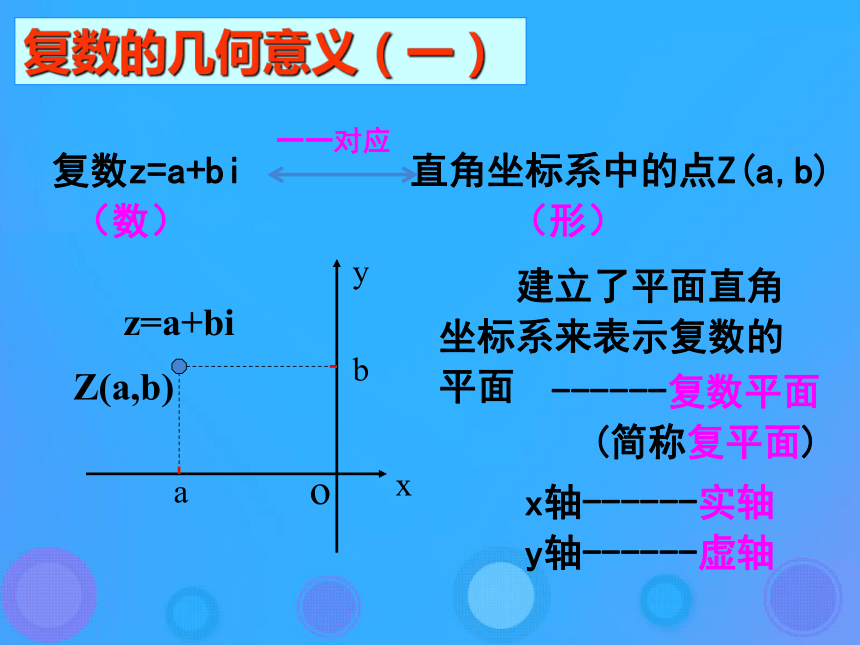
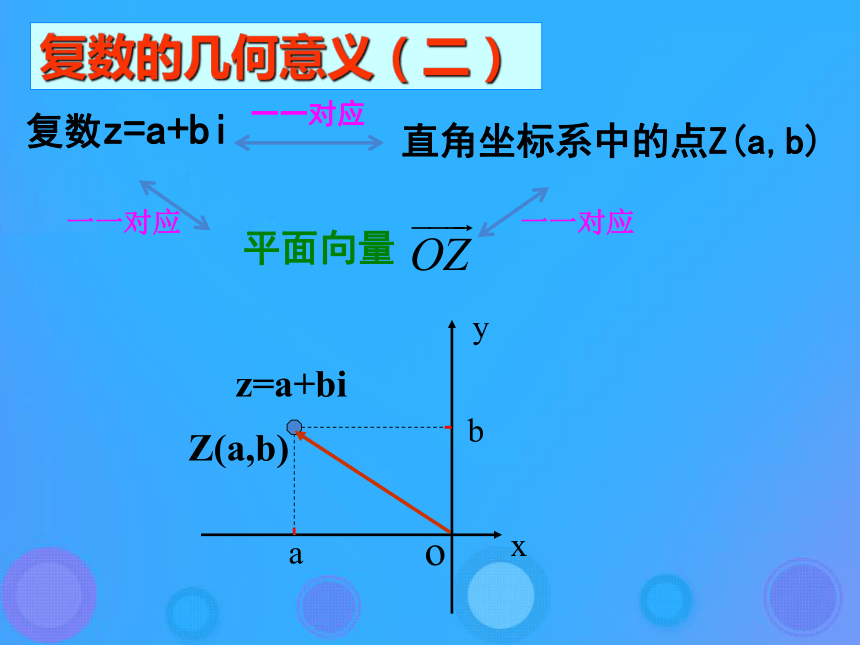
2、复数Z1=a1+b1i与Z2=a2+b2i 相等的充要条件是_____________。a1=a2,b1=b2a+bi (a,b∈R)实部和虚部a=0,b≠0b=0a ≠ 0,b≠0引例:已知 ,其中解题思考:复数相等转化求方程组的解的问题一种重要的数学思想:转化思想求x与y? 同样的转化思想我们在哪里还遇见过?思考?向量相等转化求方程组的解的问题复数z=a+bi直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------复数平面 (简称复平面)一一对应z=a+bi复数的几何意义(一)复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应复数的几何意义(二)xyobaZ(a,b)z=a+bixOz=a+biy复数的绝对值(复数的模)的几何意义:Z (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = y复数的共轭z=a+bi的共轭复数 z=a-bi例1:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围。 一种重要的数学思想:数形结合思想练习:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。 解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2), ∴(m2+m-6)-2(m2+m-2)+4=0, ∴m=1或m=-2。 例2:求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i(4)z4=1+mi(m∈R)
(5)z5=4a-3ai(a<0)( 5 )( 5 )(-5a )xyO设z=x+yi(x,y∈R)例3.满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–5图形:以原点为圆心,5为半径的圆上5xyO设z=x+yi(x,y∈R)变式:.
满足3<|z|<5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–53–3–33图形:以原点为圆心, 半径3至5的圆环内变式:已知复数m=2-3i,若复数z满足不等式|z-m|=1,则z所对应的点的集合是什么图形?以点(2, -3)为圆心,
1为半径的圆上已知复数 ,
求以下各式取值范围
(1)
(2)
(3)
?
例题解析
实数 非纯虚数
2、复数Z1=a1+b1i与Z2=a2+b2i 相等的充要条件是_____________。a1=a2,b1=b2a+bi (a,b∈R)实部和虚部a=0,b≠0b=0a ≠ 0,b≠0复数的几何意义知识回顾1、复数的概念:形如______________的数叫做复数,a,b分别叫做它的_____________。为纯虚数
实数 非纯虚数
2、复数Z1=a1+b1i与Z2=a2+b2i 相等的充要条件是_____________。a1=a2,b1=b2a+bi (a,b∈R)实部和虚部a=0,b≠0b=0a ≠ 0,b≠0引例:已知 ,其中解题思考:复数相等转化求方程组的解的问题一种重要的数学思想:转化思想求x与y? 同样的转化思想我们在哪里还遇见过?思考?向量相等转化求方程组的解的问题复数z=a+bi直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------复数平面 (简称复平面)一一对应z=a+bi复数的几何意义(一)复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应复数的几何意义(二)xyobaZ(a,b)z=a+bixOz=a+biy复数的绝对值(复数的模)的几何意义:Z (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = y复数的共轭z=a+bi的共轭复数 z=a-bi例1:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围。 一种重要的数学思想:数形结合思想练习:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值。 解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2), ∴(m2+m-6)-2(m2+m-2)+4=0, ∴m=1或m=-2。 例2:求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i(4)z4=1+mi(m∈R)
(5)z5=4a-3ai(a<0)( 5 )( 5 )(-5a )xyO设z=x+yi(x,y∈R)例3.满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–5图形:以原点为圆心,5为半径的圆上5xyO设z=x+yi(x,y∈R)变式:.
满足3<|z|<5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–53–3–33图形:以原点为圆心, 半径3至5的圆环内变式:已知复数m=2-3i,若复数z满足不等式|z-m|=1,则z所对应的点的集合是什么图形?以点(2, -3)为圆心,
1为半径的圆上已知复数 ,
求以下各式取值范围
(1)
(2)
(3)
?
例题解析
