高中数学第一章导数及其应用1.1.1函数的平均变化率课件 新人教B版选修2_2(19张PPT)
文档属性
| 名称 | 高中数学第一章导数及其应用1.1.1函数的平均变化率课件 新人教B版选修2_2(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 375.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-23 15:13:17 | ||
图片预览






文档简介
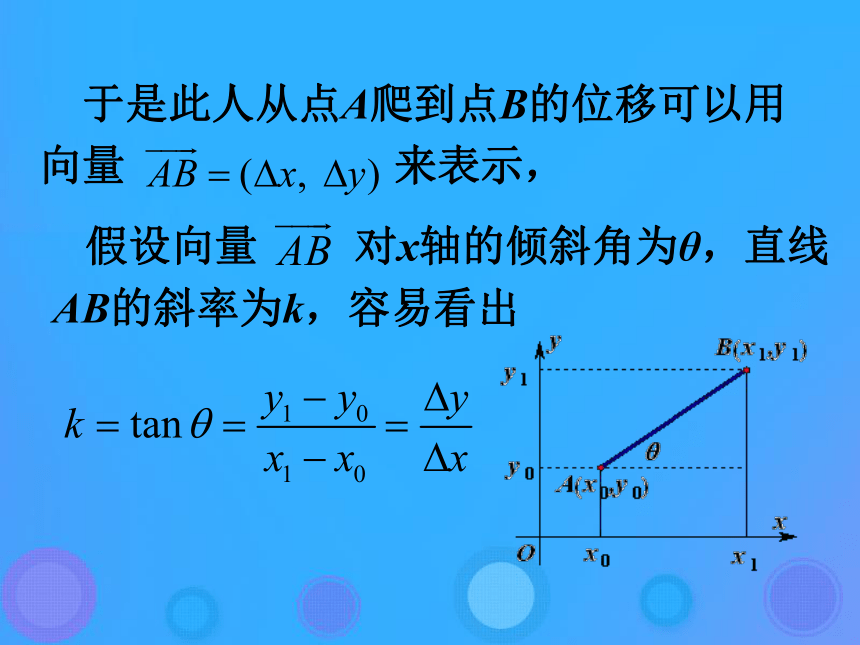
课件19张PPT。 函数的平均变化率例子 : 假设下图是一座山的剖面示意图,并在上面建立平面直角坐标系。A是出发点,H是山顶。爬山路线用函数y=f(x)表示。H 自变量x表示某旅游者的水平位置,函数值y=f(x)表示此时旅游者所在的高度。想想看,如何用数量表示此旅游者登山路线的平缓及陡峭程度呢? 某旅游者从A点爬到B点,假设这段山路是平直的。设点A的坐标为(x0,y0),点B的坐标为(x1,y1),自变量x的改变量为x1-x0,记作△x,函数值的改变量为y1-y0,记作△y,即△x=x1-x0,△y=y1-y0, 假设向量 对x轴的倾斜角为θ,直线AB的斜率为k,容易看出 于是此人从点A爬到点B的位移可以用向量 来表示, 显然,“线段”所在直线的斜率的绝对值越大,山坡越陡。这就是说,竖直位移与水平位移之比 的绝对值越大,山坡越陡;反之,山坡越平缓。 现在摆在我们面前的问题是:山路是弯曲的,怎样用数量刻画弯曲山路的陡峭程度呢? 一个很自然的想法是将弯曲的山路分成许多小段,每一小段的山坡可视为平直的。例如,山坡DE可近似的看作线段DE,再用对平直山坡AB分析的方法,得到此段山路的陡峭程度可以用比值近似地刻画。 注意各小段的 是不尽相同的。但不管是哪一小段山坡,高度的平均变化都可以用起点、终点的纵坐标之差与横坐标之差的比值 来度量。由此我们引出函数平均变化率的概念。 平均变化率的概念: 一般地,已知函数y=f(x),x0,x1是其定义域内不同的两点,记△x=x1-x0,△y=y1-y0=f(x1)-f(x0)=f(x0+△x)-f(x0). 则当△x≠0时,商
称作函数y=f(x)在区间[x0,x0+△x](或[x0+△x,x0])的平均变化率。说明:
1.函数y=f(x)在 处有定义;
2.式子中△x 、△y的值可正、可负,但的△x值不能为0, △y 的值可以为0;
3.若函数f (x)为常函数时, △y=0;
4. 变式:函数平均变化率的几何意义过曲线 上的点
割线的斜率。例1.求函数y=x2在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率。解:函数y=x2在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率为例2.求函数 在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率(x0≠0,且x0+△x≠0).解:函数 的平均变化率为 达标练习1.设函数y=f(x),当自变量x由x0改变到x0+△x时,函数的改变量为( )
A.f(x0+△x) B. f(x0)+△x
C.f(x0 ) ·△x D.f(x0+△x) -f(x0)D 2. 一质点运动的方程为s=1-2t2,则在一段时间[1,2]内的平均速度为( )
A.-4 B.-8
C. -6 D.6C3. 将半径为R的球加热,若球的半径增加△R,则球的表面积增加△S等于( )
A. B.
C. D.B4、在附近,取,在四个函数:①② ④ 中,平均变化率最大的是( )
A、④ B、③ C、② D、①③B5、过曲线y=f(x)=x3上两点P(1,1)和Q (1+Δx,1+Δy)作曲线的割线,求出当Δx=0.1时割线的斜率.课堂小结1、平均变化率的概念: 一般地,已知函数y=f(x),x0,x1是其定义域内不同的两点,记△x=x1-x0,△y=y1-y0=f(x1)-f(x0)=f(x0+△x)-f(x0). 则当△x≠0时,商
称作函数y=f(x)在区间[x0,x0+△x](或[x0+△x,x0])的平均变化率。
2.式子中△x 、△y的值可正、可负,但的△x值不能为0, △y 的值可以为0;
3.若函数f (x)为常函数时, △y=0;
4. 变式:
称作函数y=f(x)在区间[x0,x0+△x](或[x0+△x,x0])的平均变化率。说明:
1.函数y=f(x)在 处有定义;
2.式子中△x 、△y的值可正、可负,但的△x值不能为0, △y 的值可以为0;
3.若函数f (x)为常函数时, △y=0;
4. 变式:函数平均变化率的几何意义过曲线 上的点
割线的斜率。例1.求函数y=x2在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率。解:函数y=x2在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率为例2.求函数 在区间[x0,x0+△x] (或[x0+△x,x0])的平均变化率(x0≠0,且x0+△x≠0).解:函数 的平均变化率为 达标练习1.设函数y=f(x),当自变量x由x0改变到x0+△x时,函数的改变量为( )
A.f(x0+△x) B. f(x0)+△x
C.f(x0 ) ·△x D.f(x0+△x) -f(x0)D 2. 一质点运动的方程为s=1-2t2,则在一段时间[1,2]内的平均速度为( )
A.-4 B.-8
C. -6 D.6C3. 将半径为R的球加热,若球的半径增加△R,则球的表面积增加△S等于( )
A. B.
C. D.B4、在附近,取,在四个函数:①② ④ 中,平均变化率最大的是( )
A、④ B、③ C、② D、①③B5、过曲线y=f(x)=x3上两点P(1,1)和Q (1+Δx,1+Δy)作曲线的割线,求出当Δx=0.1时割线的斜率.课堂小结1、平均变化率的概念: 一般地,已知函数y=f(x),x0,x1是其定义域内不同的两点,记△x=x1-x0,△y=y1-y0=f(x1)-f(x0)=f(x0+△x)-f(x0). 则当△x≠0时,商
称作函数y=f(x)在区间[x0,x0+△x](或[x0+△x,x0])的平均变化率。
2.式子中△x 、△y的值可正、可负,但的△x值不能为0, △y 的值可以为0;
3.若函数f (x)为常函数时, △y=0;
4. 变式:
