高中数学第一章导数及其应用1.1.2瞬时速度与导数课件 新人教B版选修2_2(18张PPT)
文档属性
| 名称 | 高中数学第一章导数及其应用1.1.2瞬时速度与导数课件 新人教B版选修2_2(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 400.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-23 15:14:40 | ||
图片预览






文档简介
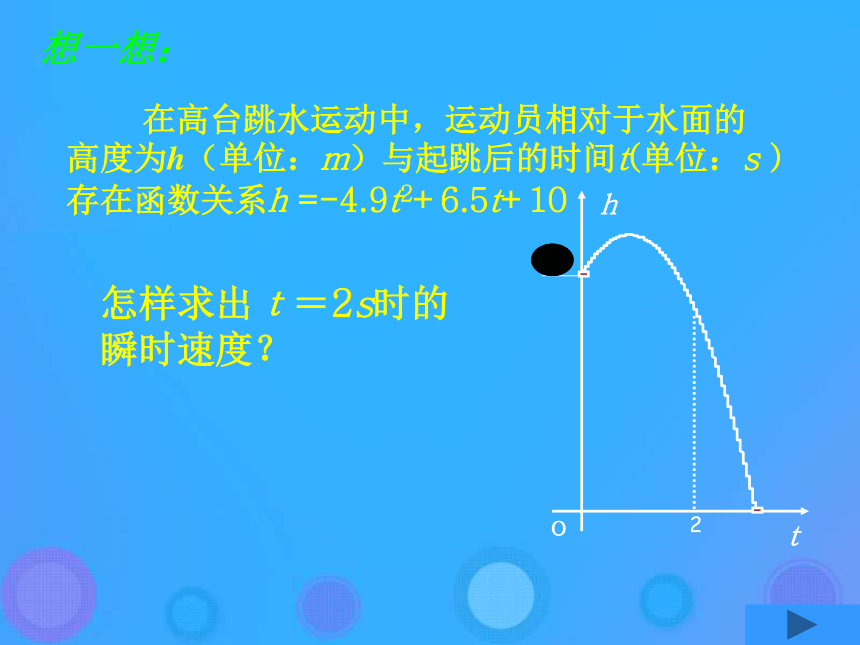
课件18张PPT。导数的概念温故知新温故知新 高台跳水(观看视频) 在高台跳水运动中, 运动员相对于水面的高度 h (单位:m)与起跳后的时间 t (单位:s) 存在函数关系 计算运动员在 这段时间里的平均速度?怎样求出t=2s时的
瞬时速度?填表思考:当Δt趋于0时,平均速度有怎样的变化趋势? 归纳整理 时间间隔 |△t |无限变小时, 平均速度就无限趋近于常数
–13.1, 这个常数被视为该运动员在 t = 2s 时的瞬时速度,即v(2)= –13.1(m/s)自主探究请阅读教材第7页至第8页上数第5自然段小组讨论:对物体在某一时刻的瞬时速度和“△t 趋近于0”的认识归纳整理定义:函数 y = f (x) 在 x = x0 处的瞬时变化率是称为函数 y = f (x) 在 x = x0 处的导数, 记作或 , 即这时又称函数 y = f (x) 在 x = x0 处是可导的概念形成如果f (x) 在 开区间(a,b)内的每一点x都是可导
的 ,则称f (x)在区间(a,b)可导。例1:变式训练1:求y=2x2+4x在点x=2和x=a处的导数例2 火箭竖直向上发射,熄火时向上的速度达到
100m/s,试问:
1)熄火后多长时间火箭向上的速度为0?
2)火箭在熄火后第5秒和第12秒的瞬时速度时多
少?变式训练2已知一个物体运动的位移S(m)与时间t(s)满足关系S(t)=-2 +5t
(1)求物体第5秒的瞬时速度
(2)求物体在t时刻的瞬时速度.
小结
1、瞬时速度的概念
2、导数的概念
3、求导数的方法:
4、思想方法:“以已知探求未知”、逼近、类比、从特殊到一般。 课后作业:2.补充题:1.必做题:P10 A组2、3、4
选做题:P10 B组1
瞬时速度?填表思考:当Δt趋于0时,平均速度有怎样的变化趋势? 归纳整理 时间间隔 |△t |无限变小时, 平均速度就无限趋近于常数
–13.1, 这个常数被视为该运动员在 t = 2s 时的瞬时速度,即v(2)= –13.1(m/s)自主探究请阅读教材第7页至第8页上数第5自然段小组讨论:对物体在某一时刻的瞬时速度和“△t 趋近于0”的认识归纳整理定义:函数 y = f (x) 在 x = x0 处的瞬时变化率是称为函数 y = f (x) 在 x = x0 处的导数, 记作或 , 即这时又称函数 y = f (x) 在 x = x0 处是可导的概念形成如果f (x) 在 开区间(a,b)内的每一点x都是可导
的 ,则称f (x)在区间(a,b)可导。例1:变式训练1:求y=2x2+4x在点x=2和x=a处的导数例2 火箭竖直向上发射,熄火时向上的速度达到
100m/s,试问:
1)熄火后多长时间火箭向上的速度为0?
2)火箭在熄火后第5秒和第12秒的瞬时速度时多
少?变式训练2已知一个物体运动的位移S(m)与时间t(s)满足关系S(t)=-2 +5t
(1)求物体第5秒的瞬时速度
(2)求物体在t时刻的瞬时速度.
小结
1、瞬时速度的概念
2、导数的概念
3、求导数的方法:
4、思想方法:“以已知探求未知”、逼近、类比、从特殊到一般。 课后作业:2.补充题:1.必做题:P10 A组2、3、4
选做题:P10 B组1
