高中数学第二章推理与证明2.3.1数学归纳法课件 新人教B版选修2_2(17张)
文档属性
| 名称 | 高中数学第二章推理与证明2.3.1数学归纳法课件 新人教B版选修2_2(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 251.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-23 00:00:00 | ||
图片预览






文档简介
课件17张PPT。2.3数学归纳法问题情境一问题 1:明朝刘元卿编的《应谐录》中有一个笑话:从前,有个小孩叫万百千,他开始上学识字。第一天先生教他个“一”字。第二天先生又教了个“二”字。第三天,他想先生一定是教“三”字了,并预先在纸上划了三横。果然这天教了个“三”字。于是他得了一个结论:“四”一定是四横,“五”一定是五横,以此类推,…从此,他不再去上学,家长发现问他为何不去上学,他自豪地说:“我都会了”。家长要他写出自己的名字,“万百千”写名字结果可想而知。” 他运用什么方法得到的结论?
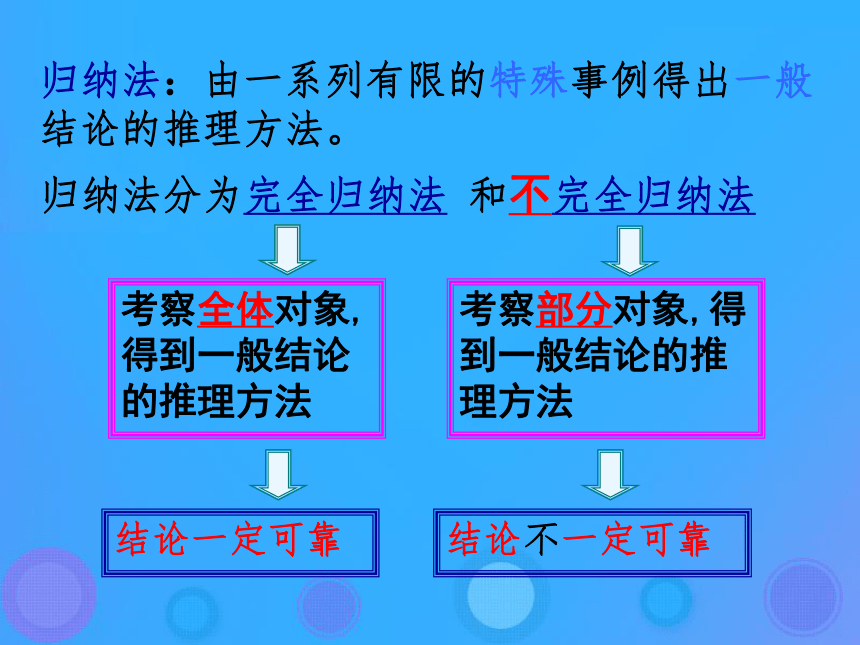
为什么会出现错误?你的猜想正确吗?如何证明呢?问题2: 在数列{}中, =1, (n∈ ), 先计算,,的值,再推测通项 的公式. 归纳法:由一系列有限的特殊事例得出一般结论的推理方法。 结论一定可靠结论不一定可靠考察全体对象,得到一般结论的推理方法考察部分对象,得到一般结论的推理方法归纳法分为完全归纳法 和不完全归纳法二、数学归纳法多米诺骨牌效应多米诺骨牌都倒下的关键点是什么?二、数学归纳法多米诺骨牌效应1.使第一张牌能倒下;
2.假设第k张能倒下,则一定能压倒紧挨的第k+1张牌。类比多米诺骨牌依顺序倒下的原理,探究出证明有关正整数命题的方法一般地,证明一个与正整数有关的命题,可按下列步骤进行: ( 2 ) 假设n = k ( k ≥ n0 ,k ∈ N* ) 时命题成立,
证明当n=k+1时命题也成立。 只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数
都成立。上述证明方法叫做数学归纳法(1) 证明当n取第一个值 n0 时命题成立。(归纳基础)( 归纳递推 )数学归纳法 证明:从n=k到n=k+1的变化凑假设凑结论三、例题讲解:四:疑点解析
用数学归纳法证明
1+3+5+ …+(2n-1)= 哪错了?用数学归纳法证明
1+3+5+ …+(2n-1)= 证明:假设n=k时等式成立,即那么即n=k+1时等式成立。所以等式对一切正整数n均成立。五、练习巩固1.用数学归纳法证明
1+3+5+ …+(2n-1)= n2 可否改换为:
1+3+5+……+(2k-1)+[2(k+1)-1]
= 1+3+5+……+(2k-1)+(2k+1)
= = (k+1)2
问:第②步中当n=k+1时:1+3+5+……+(2k-1)+[2(k+1)-1]
=k2+2k+1 = (k+1)2 , 所以当n=k+1时等式也成立;2. 证明凸n边形内角和为 中, 初始值应该从几取?初始值应取3
四:巩固提高课堂小结1、数学归纳法能够解决哪一类问题?
2、数学归纳法证明命题的步骤是什么?
3、应用数学归纳法证明命题应注意什么问题?
一般被应用于证明某些与正整数有关的数学命题。两个步骤和一个结论,缺一不可。(1)第一步是证明的基础,必不可少。
(2)初始值不一定为1。
(3)第二步证明时必须要用到假设。作业1、教材P96 A组1(1)(3)
2、查阅资料皮亚诺公理(数学归纳法的理论根据)谢谢大家欢迎各位老师提出宝贵意见在应用数学归纳法时,应该注意哪些问题?(1)第一步是证明的基础,必须先验证初始值是否成立。(2)初始值不一定是1,而是使命题成立的第一个正整数。(3)第2步证明中,必须用到假设的结论。
为什么会出现错误?你的猜想正确吗?如何证明呢?问题2: 在数列{}中, =1, (n∈ ), 先计算,,的值,再推测通项 的公式. 归纳法:由一系列有限的特殊事例得出一般结论的推理方法。 结论一定可靠结论不一定可靠考察全体对象,得到一般结论的推理方法考察部分对象,得到一般结论的推理方法归纳法分为完全归纳法 和不完全归纳法二、数学归纳法多米诺骨牌效应多米诺骨牌都倒下的关键点是什么?二、数学归纳法多米诺骨牌效应1.使第一张牌能倒下;
2.假设第k张能倒下,则一定能压倒紧挨的第k+1张牌。类比多米诺骨牌依顺序倒下的原理,探究出证明有关正整数命题的方法一般地,证明一个与正整数有关的命题,可按下列步骤进行: ( 2 ) 假设n = k ( k ≥ n0 ,k ∈ N* ) 时命题成立,
证明当n=k+1时命题也成立。 只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数
都成立。上述证明方法叫做数学归纳法(1) 证明当n取第一个值 n0 时命题成立。(归纳基础)( 归纳递推 )数学归纳法 证明:从n=k到n=k+1的变化凑假设凑结论三、例题讲解:四:疑点解析
用数学归纳法证明
1+3+5+ …+(2n-1)= 哪错了?用数学归纳法证明
1+3+5+ …+(2n-1)= 证明:假设n=k时等式成立,即那么即n=k+1时等式成立。所以等式对一切正整数n均成立。五、练习巩固1.用数学归纳法证明
1+3+5+ …+(2n-1)= n2 可否改换为:
1+3+5+……+(2k-1)+[2(k+1)-1]
= 1+3+5+……+(2k-1)+(2k+1)
= = (k+1)2
问:第②步中当n=k+1时:1+3+5+……+(2k-1)+[2(k+1)-1]
=k2+2k+1 = (k+1)2 , 所以当n=k+1时等式也成立;2. 证明凸n边形内角和为 中, 初始值应该从几取?初始值应取3
四:巩固提高课堂小结1、数学归纳法能够解决哪一类问题?
2、数学归纳法证明命题的步骤是什么?
3、应用数学归纳法证明命题应注意什么问题?
一般被应用于证明某些与正整数有关的数学命题。两个步骤和一个结论,缺一不可。(1)第一步是证明的基础,必不可少。
(2)初始值不一定为1。
(3)第二步证明时必须要用到假设。作业1、教材P96 A组1(1)(3)
2、查阅资料皮亚诺公理(数学归纳法的理论根据)谢谢大家欢迎各位老师提出宝贵意见在应用数学归纳法时,应该注意哪些问题?(1)第一步是证明的基础,必须先验证初始值是否成立。(2)初始值不一定是1,而是使命题成立的第一个正整数。(3)第2步证明中,必须用到假设的结论。
