高中数学第三章数系的扩充与复数3.1.3复数的几何意义课件 新人教B版选修2_2(19张)
文档属性
| 名称 | 高中数学第三章数系的扩充与复数3.1.3复数的几何意义课件 新人教B版选修2_2(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-23 17:48:01 | ||
图片预览





文档简介
课件19张PPT。《复数的几何意义》1.复数Z=a+bi(a, b∈R),复数的实部和虚部各是什么?
2.平面向量及其模的概念是什么?如何计算模?
3.实数与数轴上的点具有怎样的对应关系?
【思考1】
实数可用数轴上的点来表示,类比一下,复数可用什 么来表示?
【提示】:
任何一个复数z=a+bi,都和一个有序实数对(a,b)一一对应,因此复数集与平面直角坐标系中的点集可以建立一一对应关系.
(1)定义: 来表示复数的 平面叫做复平面.
(2)实轴:在复平面内 叫做实轴,单位是______,实轴上的点都表示 .
(3)虚轴:在复平面内 叫做虚轴,单位是____,除 外,虚轴上的点都表示 .
(4)原点:原点(0,0)表示 .建立了直角坐标系x轴1实数y轴i原点纯虚数复数0一、复平面(A)复平面内,对应实数的点都在实轴上
(B)复平面内,对应纯虚数的点都在虚轴上
(C)复平面内,实轴上的点所对应的复数都
是实数
(D)复平面内,虚轴上的点所对应的复数
都是纯虚数。1.下列命题中的假命题是( )D注意:实轴上的点都表示 ,除原点
以外,虚轴上的点都表示 , 象限
中的点都表示 .实数纯虚数非纯虚数 练习1 1.复数与复平面内的点有怎样的对应关系?
一一对应关系.
2.复数与复平面内以原点为起点的向量有怎样的对应关系?
一一对应关系.
3.平面向量能够与复数一一对应的前提 是什么?
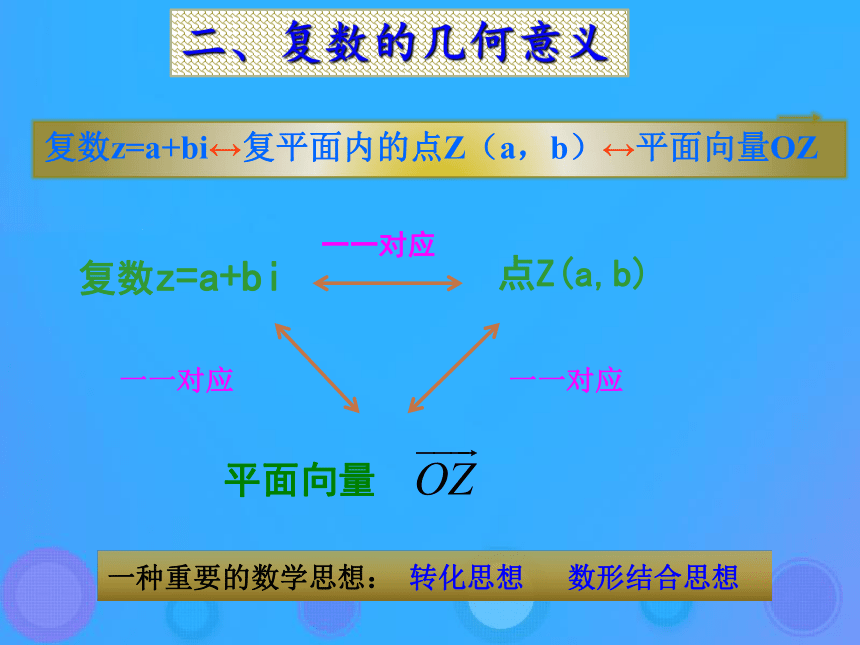
向量的起点在原点.二、复数的几何意义二、复数的几何意义复数z=a+bi点Z(a,b)一一对应一一对应一一对应一种重要的数学思想: 转化思想 数形结合思想实数绝对值的几何意义能否把实数绝对值概念
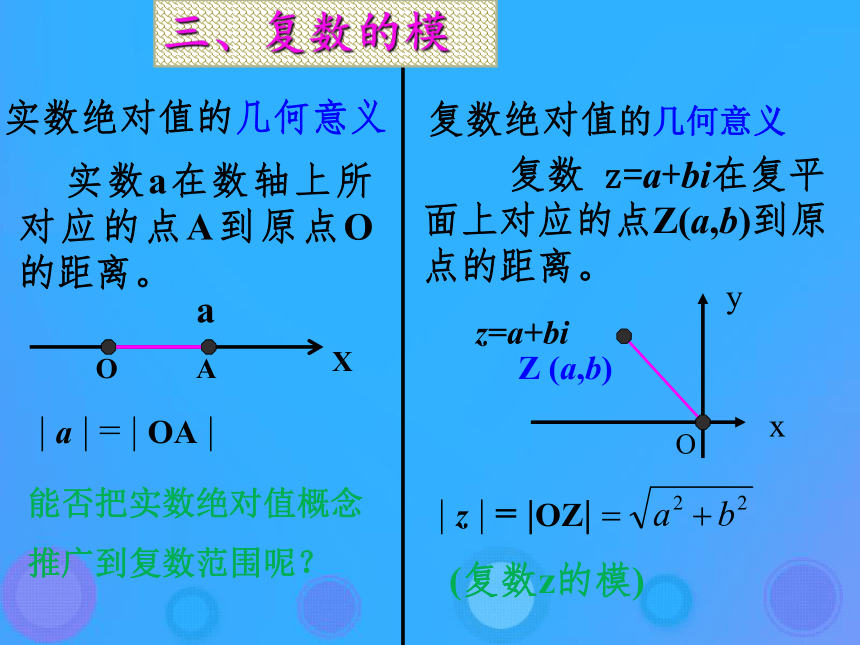
推广到复数范围呢? 实数a在数轴上所对应的点A到原点O的距离。复数绝对值的几何意义 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。三、复数的模 2.求下列复数的模:
(1)z1=-4i (2)z2=-3+4i
(3)z3=-3-4i
(5)z5=3-4i(4)z4=1+mi(m∈R)
(6)z6=4a-3ai(a<0)练习2
思考1:(2)比较|-3+4i|与|3-4i|的大小.
(3)比较|-3+4i|与|-3-4i|的大小.(1)复数的模能否比较大小?四、共轭复数 定义:当两个复数的实部相等,虚部互为相反数时,
这两个复数叫做互为共轭复数.若z=a+bi(a、b∈R)则其共轭复数为:注意:1.实数的共轭复数是 它本身2.两共轭复数的点 .关于实轴对称 B练习3:例1:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围。 五、课堂互动探究(一)复数的几何意义:复数与复平面内的点的关系 (1)在复平面内,复数z=sin 2+icos 2对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限D9【思路探究】(1)判断复数z实部、虚部与0的关系.(2)找出复数z的实部与虚部,令它们相等,求m.练习4:设z=x+yi(x,y∈R)图形:以原点为圆心,5为半径的圆思考2:1.满足|z|=5(z∈R)的z值有几个?2.满足|z|=5(z∈C)的z值有几个? 这些复数对应的点在复平面上构成怎样的图形?设z=x+yi(x,y∈R)例2.满足3<|z|<5(z∈C)
的复数z对应的点在复平
面上将构成怎样的图形?图形:以原点为圆心,半径3至5的圆环内(二)复数的模几何意义的应用满足 (z∈C)的复数z对应的点Z的集合是什么图形?思考3: (三)复数模的计算与应用例3 以(-1,2)为圆心,3为半径的圆B(1)把|z|用a表示,再根据a的范围求|z|的范围.
(2)根据|z|=3写出关于x,y的方程,再判断轨迹.【思路探究】一、选择题
1.在复平面内,复数Z=i+ i2表示的点在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2.复数i+2i2的共轭复数是 ( )
A.2+i B.2-i C.-2+i D.-2-i
3.满足条件|z|=|3+4i|的复数z在复平面上对应的点Z的
轨迹是( )
A.一条直线 B.两条直线 C.圆 D.椭圆BDC
4、复数2-3i对应的点所在的直线是 ( )
A.y=x B.y=-x C.3x+2y=0 D.2x+3y=0
5.在复平面内,复数z=1-i对应的点的坐标为( )
A.(1,i) B.(1,-i) C.(1, 1) D.(1,-1)
二、填空题:
6、复数Z=(x-1)+(2x-1)i的模小于 ,则实数x的取
值范围是
7、已知Z= x+2+( y-1)i的模为 ,则点(x, y)的
轨迹方程 ( )是
C D课堂小结:1.知识归纳:
2.思想方法归纳:1. 知识归纳:2. 思想方法归纳:(1)复数的几何意义(2)复数的模类比思想数形结合思想(1) 转化思想(3)共轭复数课堂小结:(2)求模的方法作业:
2.平面向量及其模的概念是什么?如何计算模?
3.实数与数轴上的点具有怎样的对应关系?
【思考1】
实数可用数轴上的点来表示,类比一下,复数可用什 么来表示?
【提示】:
任何一个复数z=a+bi,都和一个有序实数对(a,b)一一对应,因此复数集与平面直角坐标系中的点集可以建立一一对应关系.
(1)定义: 来表示复数的 平面叫做复平面.
(2)实轴:在复平面内 叫做实轴,单位是______,实轴上的点都表示 .
(3)虚轴:在复平面内 叫做虚轴,单位是____,除 外,虚轴上的点都表示 .
(4)原点:原点(0,0)表示 .建立了直角坐标系x轴1实数y轴i原点纯虚数复数0一、复平面(A)复平面内,对应实数的点都在实轴上
(B)复平面内,对应纯虚数的点都在虚轴上
(C)复平面内,实轴上的点所对应的复数都
是实数
(D)复平面内,虚轴上的点所对应的复数
都是纯虚数。1.下列命题中的假命题是( )D注意:实轴上的点都表示 ,除原点
以外,虚轴上的点都表示 , 象限
中的点都表示 .实数纯虚数非纯虚数 练习1 1.复数与复平面内的点有怎样的对应关系?
一一对应关系.
2.复数与复平面内以原点为起点的向量有怎样的对应关系?
一一对应关系.
3.平面向量能够与复数一一对应的前提 是什么?
向量的起点在原点.二、复数的几何意义二、复数的几何意义复数z=a+bi点Z(a,b)一一对应一一对应一一对应一种重要的数学思想: 转化思想 数形结合思想实数绝对值的几何意义能否把实数绝对值概念
推广到复数范围呢? 实数a在数轴上所对应的点A到原点O的距离。复数绝对值的几何意义 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。三、复数的模 2.求下列复数的模:
(1)z1=-4i (2)z2=-3+4i
(3)z3=-3-4i
(5)z5=3-4i(4)z4=1+mi(m∈R)
(6)z6=4a-3ai(a<0)练习2
思考1:(2)比较|-3+4i|与|3-4i|的大小.
(3)比较|-3+4i|与|-3-4i|的大小.(1)复数的模能否比较大小?四、共轭复数 定义:当两个复数的实部相等,虚部互为相反数时,
这两个复数叫做互为共轭复数.若z=a+bi(a、b∈R)则其共轭复数为:注意:1.实数的共轭复数是 它本身2.两共轭复数的点 .关于实轴对称 B练习3:例1:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围。 五、课堂互动探究(一)复数的几何意义:复数与复平面内的点的关系 (1)在复平面内,复数z=sin 2+icos 2对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限D9【思路探究】(1)判断复数z实部、虚部与0的关系.(2)找出复数z的实部与虚部,令它们相等,求m.练习4:设z=x+yi(x,y∈R)图形:以原点为圆心,5为半径的圆思考2:1.满足|z|=5(z∈R)的z值有几个?2.满足|z|=5(z∈C)的z值有几个? 这些复数对应的点在复平面上构成怎样的图形?设z=x+yi(x,y∈R)例2.满足3<|z|<5(z∈C)
的复数z对应的点在复平
面上将构成怎样的图形?图形:以原点为圆心,半径3至5的圆环内(二)复数的模几何意义的应用满足 (z∈C)的复数z对应的点Z的集合是什么图形?思考3: (三)复数模的计算与应用例3 以(-1,2)为圆心,3为半径的圆B(1)把|z|用a表示,再根据a的范围求|z|的范围.
(2)根据|z|=3写出关于x,y的方程,再判断轨迹.【思路探究】一、选择题
1.在复平面内,复数Z=i+ i2表示的点在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2.复数i+2i2的共轭复数是 ( )
A.2+i B.2-i C.-2+i D.-2-i
3.满足条件|z|=|3+4i|的复数z在复平面上对应的点Z的
轨迹是( )
A.一条直线 B.两条直线 C.圆 D.椭圆BDC
4、复数2-3i对应的点所在的直线是 ( )
A.y=x B.y=-x C.3x+2y=0 D.2x+3y=0
5.在复平面内,复数z=1-i对应的点的坐标为( )
A.(1,i) B.(1,-i) C.(1, 1) D.(1,-1)
二、填空题:
6、复数Z=(x-1)+(2x-1)i的模小于 ,则实数x的取
值范围是
7、已知Z= x+2+( y-1)i的模为 ,则点(x, y)的
轨迹方程 ( )是
C D课堂小结:1.知识归纳:
2.思想方法归纳:1. 知识归纳:2. 思想方法归纳:(1)复数的几何意义(2)复数的模类比思想数形结合思想(1) 转化思想(3)共轭复数课堂小结:(2)求模的方法作业:
