高中数学第三章数系的扩充与复数3.2.2复数的乘法课件5新人教B版选修2_2(18张)
文档属性
| 名称 | 高中数学第三章数系的扩充与复数3.2.2复数的乘法课件5新人教B版选修2_2(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 360.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-23 17:50:08 | ||
图片预览




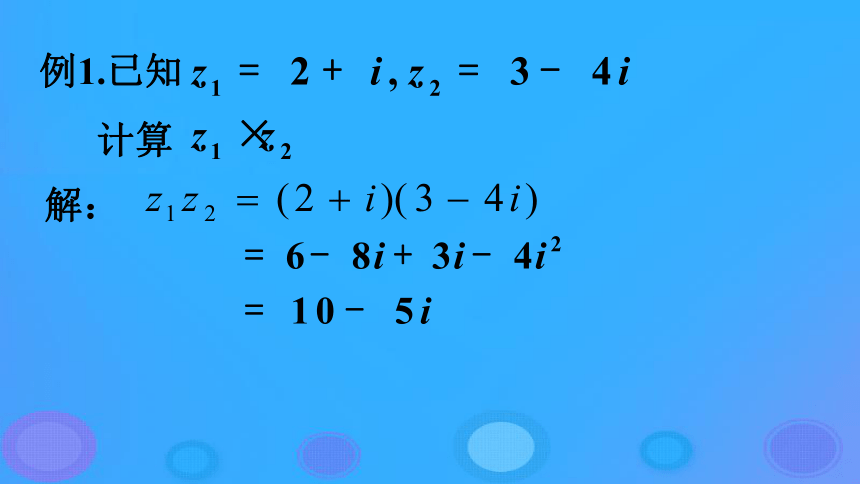


文档简介
课件18张PPT。3.2.2 复数的乘法3.2.2 复数的乘法设z1=a+bi,z2=c+di (a、b、c、d∈R) (a+bi)+(c+di)=(a+c)+(b+d)i1、复数的加法法则:2、复数的减法法则:复习引入 两个复数的乘法可以按照多项式的乘法运算来进行,只是在遇到 i2 时,要把 i2 换成-1,并把最后的结果写成 (a,b∈R) 的形式。一、复数的乘法: 设z1=a+bi,z2=c+di,a,b,c,d∈R,定义z1z2=(ac-bd)+(ad+bc)i二.复数乘法运算律:交换律: 结合律: 分配律: z1·z2=z2·z1(z1·z2) ·z3=z1·(z2·z3)z1· (z2+z3)=z1·z2+z1·z3例1.已知
计算解: 例2.求证:证明:设 则 于是结论:两个共轭复数的乘积等于这个复数(或其共轭复数)模的平方.(3)求证:实数集R中正整数指数的运算律,在复数集C中仍然成立.即对z,z1,z2∈C及m,n∈N*有: (z1z2)n=z1nz2nzmzn=zm+n (zm)n=zmn 三.复数的指数幂运算:四. i 的指数变化规律:你能发现规律吗?有怎样的规律?例3.计算解: 例4.计算: i37, i28, i19, i90. 解:i37=i4×9+1=i i28=i4×7=1 i19=i4×4+3=-i i90=i4×22+2=-1例5.计算: (1)(1+i)2; (2)(1-i)2; (3)(1+i)2000 解: (1) (1+i)2=12+2·1·i+i2=1+2i-1=2i (2) (1-i)2=12-2·1·i+i2=1-2i-1=-2i (3) (1+i)2000=[(1+i)2]1000=(2i)1000
=21000·i1000=21000·1=210001.求值:【2017江苏,2】 已知复数
其中i是虚数单位,则z的模是 .
【答案】 【2017山东,理2】已知,i是虚数单位,
若 ,则a=
(A)1或-(B) (C)- (D)
【答案】A得,所以
【解析】:,【2017北京,理2】若复数
在复平面内对应的点在第二象限,则实数a的取值范围是
(A)(–∞,1) (B)(–∞,–1)
(C)(1,+∞) (D)(–1,+∞)
【答案】B
【解析】
小 结 一、复数的乘法
二、复数的运算律
三、复数的指数幂运算
四、 i 的指数变化规律
计算解: 例2.求证:证明:设 则 于是结论:两个共轭复数的乘积等于这个复数(或其共轭复数)模的平方.(3)求证:实数集R中正整数指数的运算律,在复数集C中仍然成立.即对z,z1,z2∈C及m,n∈N*有: (z1z2)n=z1nz2nzmzn=zm+n (zm)n=zmn 三.复数的指数幂运算:四. i 的指数变化规律:你能发现规律吗?有怎样的规律?例3.计算解: 例4.计算: i37, i28, i19, i90. 解:i37=i4×9+1=i i28=i4×7=1 i19=i4×4+3=-i i90=i4×22+2=-1例5.计算: (1)(1+i)2; (2)(1-i)2; (3)(1+i)2000 解: (1) (1+i)2=12+2·1·i+i2=1+2i-1=2i (2) (1-i)2=12-2·1·i+i2=1-2i-1=-2i (3) (1+i)2000=[(1+i)2]1000=(2i)1000
=21000·i1000=21000·1=210001.求值:【2017江苏,2】 已知复数
其中i是虚数单位,则z的模是 .
【答案】 【2017山东,理2】已知,i是虚数单位,
若 ,则a=
(A)1或-(B) (C)- (D)
【答案】A得,所以
【解析】:,【2017北京,理2】若复数
在复平面内对应的点在第二象限,则实数a的取值范围是
(A)(–∞,1) (B)(–∞,–1)
(C)(1,+∞) (D)(–1,+∞)
【答案】B
【解析】
小 结 一、复数的乘法
二、复数的运算律
三、复数的指数幂运算
四、 i 的指数变化规律
