高中数学第一章导数及其应用1.3.1利用导数判断函数的单调性课件 新人教B版选修2_2
文档属性
| 名称 | 高中数学第一章导数及其应用1.3.1利用导数判断函数的单调性课件 新人教B版选修2_2 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-23 00:00:00 | ||
图片预览








文档简介
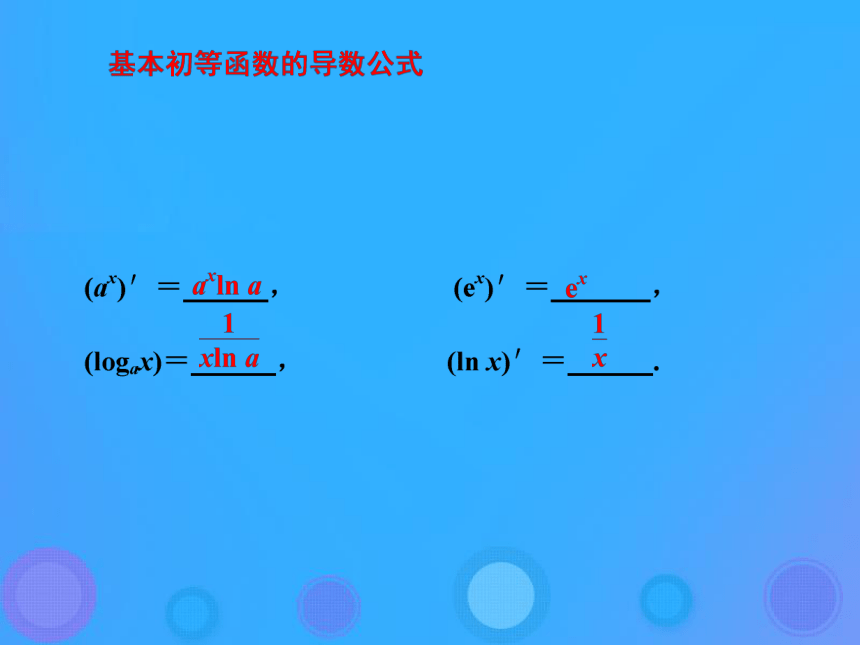
课件23张PPT。1.3.1利用导数求函数的单调区间1. 掌握导数与函数单调性之间的关系,会利用导数研究函数的单调性,会求不超过三次的多项式函数的单调区间;
2.会求含参数的函数的单调区间;
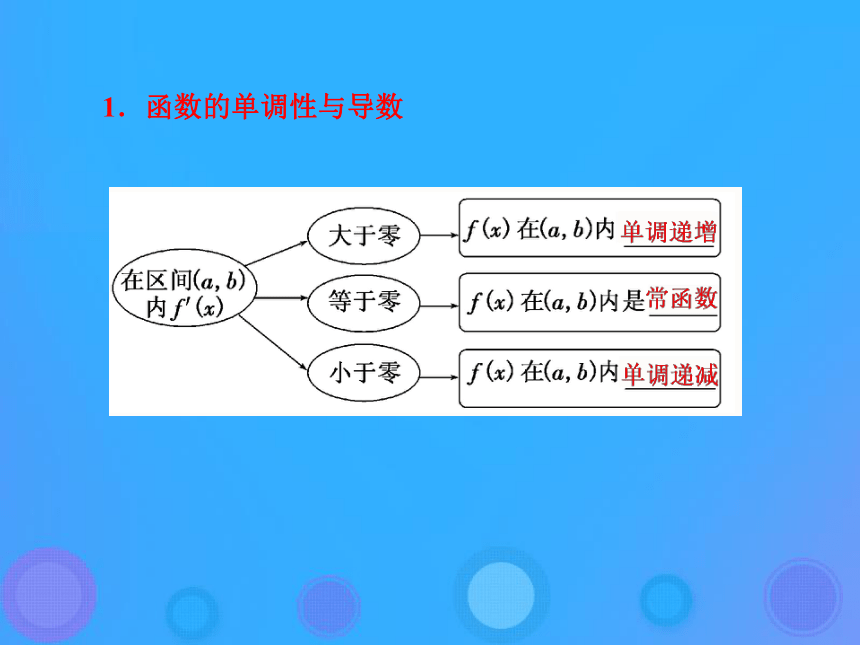
3.会根据函数的单调区间求参数的取值范围。一、课标要求1.函数的单调性与导数 探究:若函数f(x)在(a,b)内单调递增,那么一定有f′(x)>0吗?f′(x)>0是否是f(x)在(a,b)内单调递增的充要条件?
提示:函数f(x)在(a,b)内单调递增,则f′(x)≥0,
f′(x)>0是f(x)在(a,b)内单调递增的充分不必要条件.
例题解析导数法证明函数f(x)在(a,b)内的单调性的步骤:
(1)求f′(x);
(2)确认f′(x)在(a,b)内的符号;.
(3)作出结论:f′(x)>0时为增函数;f′(x)<0时为减函数.
针对训练D课堂小结:本节课探讨了利用导数求函数的单调区间1、利用导数求函数单调区间的步骤:2、导数法证明函数f(x)在(a,b)内的单调性的步骤:
(1)求f′(x);
(2)确认f′(x)在(a,b)内的符号;.
(3)作出结论:f′(x)>0时为增函数;f′(x)<0时为减函数.
作业:(1)将1中第(2)问中的“a>0”去掉,其他条件不变,求函数f(x)的单调区间;
(2)将1中第(3)问改为“g(x)在区间(-2,-1)内单调递减”和“g(x)的单调区间恰为(-2,-1)”,分别求参数a的取值范围;
?变式
2.会求含参数的函数的单调区间;
3.会根据函数的单调区间求参数的取值范围。一、课标要求1.函数的单调性与导数 探究:若函数f(x)在(a,b)内单调递增,那么一定有f′(x)>0吗?f′(x)>0是否是f(x)在(a,b)内单调递增的充要条件?
提示:函数f(x)在(a,b)内单调递增,则f′(x)≥0,
f′(x)>0是f(x)在(a,b)内单调递增的充分不必要条件.
例题解析导数法证明函数f(x)在(a,b)内的单调性的步骤:
(1)求f′(x);
(2)确认f′(x)在(a,b)内的符号;.
(3)作出结论:f′(x)>0时为增函数;f′(x)<0时为减函数.
针对训练D课堂小结:本节课探讨了利用导数求函数的单调区间1、利用导数求函数单调区间的步骤:2、导数法证明函数f(x)在(a,b)内的单调性的步骤:
(1)求f′(x);
(2)确认f′(x)在(a,b)内的符号;.
(3)作出结论:f′(x)>0时为增函数;f′(x)<0时为减函数.
作业:(1)将1中第(2)问中的“a>0”去掉,其他条件不变,求函数f(x)的单调区间;
(2)将1中第(3)问改为“g(x)在区间(-2,-1)内单调递减”和“g(x)的单调区间恰为(-2,-1)”,分别求参数a的取值范围;
?变式
