2018_2019高中数学第2章圆锥曲线与方程2.1圆锥曲线课件苏教版选修1_1(33张PPT)
文档属性
| 名称 | 2018_2019高中数学第2章圆锥曲线与方程2.1圆锥曲线课件苏教版选修1_1(33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 624.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-24 08:55:15 | ||
图片预览











文档简介
课件33张PPT。§2.1 圆锥曲线第2章 圆锥曲线与方程学习目标1.掌握圆锥曲线的类型及其定义、几何图形和标准方程,会求简单圆锥曲线的方程.
2.通过对圆锥曲线性质的研究,感受数形结合的基本思想和理解代数方法研究几何性质的优越性.问题导学达标检测题型探究内容索引问题导学知识点一 椭圆的定义思考 如果动点P到两定点A,B的距离之和为PA+PB=2a(a>0且a为常数),点P的轨迹一定是椭圆吗?
答案 不一定.
当2a>AB时,P点的轨迹是椭圆;
当2a=AB时,P点的轨迹是线段AB;
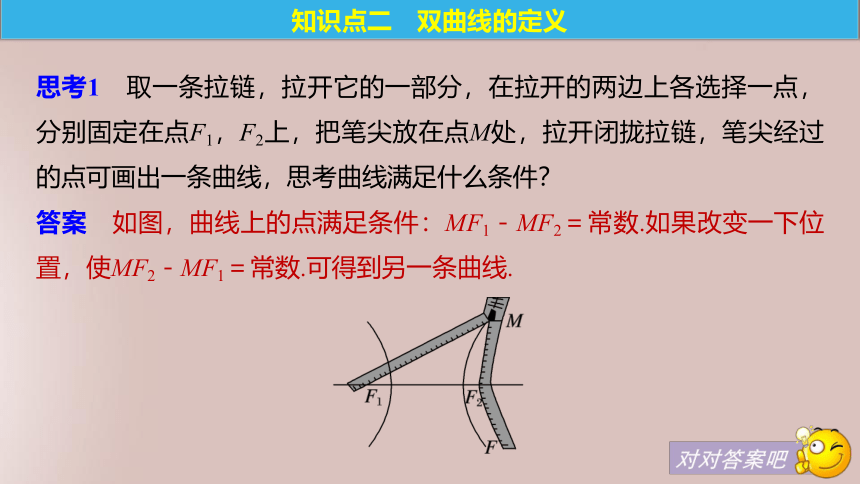
当2a答案 如图,曲线上的点满足条件:MF1-MF2=常数.如果改变一下位置,使MF2-MF1=常数.可得到另一条曲线.知识点二 双曲线的定义思考2 在双曲线的定义中强调平面内动点到两定点的距离差的绝对值为常数,若没有绝对值,则动点的轨迹是什么?为什么要限制到两定点距离之差的绝对值为常数2a,2a答案 若没有绝对值,动点的轨迹就成了双曲线的一支.
只有当2aF1F2时,满足条件的点不存在.梳理 平面内与两个定点F1,F2距离的差的绝对值等于常数(__________
)的点的轨迹叫做双曲线.这两个定点F1,F2叫做双曲线的 ,两焦点间的距离叫做双曲线的 .小于F1F2的正数焦点焦距知识点三 抛物线的定义如图,我们在黑板上画一条直线EF,然后取一个三角板,将一条拉链AB固定在三角板的一条直角边上,并将拉链下边一半的一端固定在C点,将三角板的另一条直角边贴在直线EF上,在拉锁D处放置一支粉笔,上下拖动三角板,粉笔会画出一条曲线.
思考1 画出的曲线是什么形状?
答案 抛物线.思考2 DA是点D到直线EF的距离吗?为什么?
答案 是.AB是直角三角形的一条直角边.
思考3 点D在移动过程中,满足什么条件?
答案 DA=DC.梳理 平面内到一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线.定点F叫做抛物线的 ,定直线l叫做抛物线的 .焦点准线1.设F1,F2为定点,F1F2=3,动点M满足MF1+MF2=3,则动点M的轨迹是椭圆.( )
2.已知定点M(1,1),定直线l:x=3,有一动点N,点N到M点的距离MN始终等于N点到直线l的距离,则N点的轨迹是一条抛物线.( )
3.已知A(-3,0),B(3,0),且MA-MB=8,则M点的轨迹是双曲线.( )[思考辨析 判断正误]√××题型探究例1 在△ABC中,B(-6,0),C(0,8),且sin B,sin A,sin C成等差数列.
(1)顶点A的轨迹是什么?
解 由sin B,sin A,sin C成等差数列,得sin B+sin C=2sin A.
由正弦定理,可得AC+AB=2BC.
又BC=10,所以AB+AC=20,且20>BC,
所以点A的轨迹是椭圆(除去直线BC与椭圆的交点).
(2)指出轨迹的焦点和焦距.
解 椭圆的焦点为B,C,焦距为10.类型一 椭圆定义的应用解答反思与感悟 此类题求解的关键是把已知条件转化为三角形边的关系,找到点满足的条件.注意三点要构成三角形,轨迹要除去两点.跟踪训练1 已知△ABC中,B(-3,0),C(3,0),且AB,BC,AC成等差数列.
(1)求证:点A在一个椭圆上运动;
证明 在△ABC中,由AB,BC,AC成等差数列得AB+AC=2BC=12>BC满足椭圆定义,所以点A在以B,C为焦点的椭圆上运动.证明(2)写出这个椭圆的焦点坐标.
解 焦点坐标为(-3,0),(3,0).解答类型二 双曲线定义的应用例2 如图,已知动圆C与圆F1,F2均外切(圆F1与圆
F2相离),试问:动点C的轨迹是什么曲线?
解 设动圆C的半径为R,圆F1,F2的半径分别为r1,
r2,易知CF1=R+r1,CF2=R+r2.
所以CF1-CF2=r1-r2.
又CF1-CF2=r1-r2故动圆圆心C的轨迹是以F1,F2为焦点的双曲线靠近F2的一支.解答引申探究
若把本例中“外切”换成“内切”再求解,结论如何?
解 设动圆C的半径为R,
圆F1,F2的半径分别为r1,r2.
易知CF1=R-r1,CF2=R-r2,
CF2-CF1=r1-r2故动圆圆心C的轨迹是以F1,F2为焦点的双曲线靠近F1的一支.解答反思与感悟 判断动点轨迹是双曲线应满足三个条件
(1)动点P到两定点的距离之差是否为常数.
(2)该常数是否小于两定点之间的距离.
(3)其差是否加上绝对值.跟踪训练2 在△ABC中,BC固定,顶点A移动.设BC=m,且|sin C-sin B|=
sin A,则顶点A的轨迹是什么?
解 因为|sin C-sin B|= sin A,
由正弦定理,可得|AB-AC|= BC= m,且 m所以点A的轨迹是双曲线(除去双曲线与BC的两个交点).解答类型三 抛物线定义的应用解答例3 若动圆与定圆(x-2)2+y2=1外切,又与直线x+1=0相切,求动圆圆心的轨迹.
解 如图所示,设动圆O′的半径为r,则动圆的圆
心O′到点(2,0)的距离为r+1,点O′到直线x=-1
的距离为r,从而可知点O′到点(2,0)的距离与到直线
x=-2的距离相等.由抛物线定义可知,动圆圆心O′
的轨迹是抛物线.引申探究
点P到点F(2,0)的距离比它到直线l:x=-3的距离小1,则点P的轨迹是________.
解析 将直线l:x=-3向右平移1个单位,
得直线l′:x=-2.依题意知,点P到F(2,0)的距离等于点P到l′:x=-2的距离,可见点P的轨迹是抛物线.抛物线答案解析反思与感悟 判断点的轨迹是抛物线注意应满足两点
(1)判断动点到定点与到定直线的距离相等.
(2)要特别注意定点不在定直线上.跟踪训练3 已知直线l:x+2y-3=0,点F(2,1),P为平面上一动点,过P作PE⊥l于E,PE=PF,则点P的轨迹为________.
解析 ∵点F(2,1)不在直线l上,且PE=PF,
∴点P的轨迹为抛物线.抛物线答案解析达标检测1.动点M到定点 的距离之和是2,则动点M的轨迹是______.
解析 ∵MA+MB=2>1=AB,
∴点M的轨迹是椭圆.椭圆答案12345解析123452.已知两点F1(-5,0),F2(5,0),到它们的距离的差的绝对值是6的点M的轨迹是________.
解析 ∵| MF1-MF2|=6∴点M的轨迹是双曲线.双曲线答案解析3.到定点A(4,0)和到定直线l:x=-4的距离相等的点的轨迹是________.12345答案抛物线答案解析4.动圆过点(1,0),且与直线x=-1相切,则动圆圆心的轨迹为_______. (从圆、椭圆、双曲线或抛物线中选填一个)
解析 由题意知,动圆圆心到直线x=-1的距离与到定点(1,0)的距离相等,由抛物线定义可得圆心的轨迹为抛物线.12345抛物线5.如图,已知圆A:(x+3)2+y2=100,圆A内有一定点
B(3,0).动圆P过B点且与圆A内切,设动圆P的半径为r,
试判断圆心P的轨迹.
解 由题意知A(-3,0),
PA=10-r,PB=r,
则PA+PB=10>AB=6,
满足椭圆的定义,
故点P的轨迹是以A,B两点为焦点的椭圆.解答123451.在椭圆定义中,常数>F1F2不可忽视,若常数2.在双曲线定义中,若常数>F1F2,则这样的点不存在;若常数=F1F2,则动点的轨迹是以F1,F2为端点的两条射线.
3.在抛物线定义中F?l.若F∈l,则点的轨迹是经过点F且垂直于l的直线.
2.通过对圆锥曲线性质的研究,感受数形结合的基本思想和理解代数方法研究几何性质的优越性.问题导学达标检测题型探究内容索引问题导学知识点一 椭圆的定义思考 如果动点P到两定点A,B的距离之和为PA+PB=2a(a>0且a为常数),点P的轨迹一定是椭圆吗?
答案 不一定.
当2a>AB时,P点的轨迹是椭圆;
当2a=AB时,P点的轨迹是线段AB;
当2a
只有当2a
)的点的轨迹叫做双曲线.这两个定点F1,F2叫做双曲线的 ,两焦点间的距离叫做双曲线的 .小于F1F2的正数焦点焦距知识点三 抛物线的定义如图,我们在黑板上画一条直线EF,然后取一个三角板,将一条拉链AB固定在三角板的一条直角边上,并将拉链下边一半的一端固定在C点,将三角板的另一条直角边贴在直线EF上,在拉锁D处放置一支粉笔,上下拖动三角板,粉笔会画出一条曲线.
思考1 画出的曲线是什么形状?
答案 抛物线.思考2 DA是点D到直线EF的距离吗?为什么?
答案 是.AB是直角三角形的一条直角边.
思考3 点D在移动过程中,满足什么条件?
答案 DA=DC.梳理 平面内到一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线.定点F叫做抛物线的 ,定直线l叫做抛物线的 .焦点准线1.设F1,F2为定点,F1F2=3,动点M满足MF1+MF2=3,则动点M的轨迹是椭圆.( )
2.已知定点M(1,1),定直线l:x=3,有一动点N,点N到M点的距离MN始终等于N点到直线l的距离,则N点的轨迹是一条抛物线.( )
3.已知A(-3,0),B(3,0),且MA-MB=8,则M点的轨迹是双曲线.( )[思考辨析 判断正误]√××题型探究例1 在△ABC中,B(-6,0),C(0,8),且sin B,sin A,sin C成等差数列.
(1)顶点A的轨迹是什么?
解 由sin B,sin A,sin C成等差数列,得sin B+sin C=2sin A.
由正弦定理,可得AC+AB=2BC.
又BC=10,所以AB+AC=20,且20>BC,
所以点A的轨迹是椭圆(除去直线BC与椭圆的交点).
(2)指出轨迹的焦点和焦距.
解 椭圆的焦点为B,C,焦距为10.类型一 椭圆定义的应用解答反思与感悟 此类题求解的关键是把已知条件转化为三角形边的关系,找到点满足的条件.注意三点要构成三角形,轨迹要除去两点.跟踪训练1 已知△ABC中,B(-3,0),C(3,0),且AB,BC,AC成等差数列.
(1)求证:点A在一个椭圆上运动;
证明 在△ABC中,由AB,BC,AC成等差数列得AB+AC=2BC=12>BC满足椭圆定义,所以点A在以B,C为焦点的椭圆上运动.证明(2)写出这个椭圆的焦点坐标.
解 焦点坐标为(-3,0),(3,0).解答类型二 双曲线定义的应用例2 如图,已知动圆C与圆F1,F2均外切(圆F1与圆
F2相离),试问:动点C的轨迹是什么曲线?
解 设动圆C的半径为R,圆F1,F2的半径分别为r1,
r2,易知CF1=R+r1,CF2=R+r2.
所以CF1-CF2=r1-r2.
又CF1-CF2=r1-r2
若把本例中“外切”换成“内切”再求解,结论如何?
解 设动圆C的半径为R,
圆F1,F2的半径分别为r1,r2.
易知CF1=R-r1,CF2=R-r2,
CF2-CF1=r1-r2
(1)动点P到两定点的距离之差是否为常数.
(2)该常数是否小于两定点之间的距离.
(3)其差是否加上绝对值.跟踪训练2 在△ABC中,BC固定,顶点A移动.设BC=m,且|sin C-sin B|=
sin A,则顶点A的轨迹是什么?
解 因为|sin C-sin B|= sin A,
由正弦定理,可得|AB-AC|= BC= m,且 m
解 如图所示,设动圆O′的半径为r,则动圆的圆
心O′到点(2,0)的距离为r+1,点O′到直线x=-1
的距离为r,从而可知点O′到点(2,0)的距离与到直线
x=-2的距离相等.由抛物线定义可知,动圆圆心O′
的轨迹是抛物线.引申探究
点P到点F(2,0)的距离比它到直线l:x=-3的距离小1,则点P的轨迹是________.
解析 将直线l:x=-3向右平移1个单位,
得直线l′:x=-2.依题意知,点P到F(2,0)的距离等于点P到l′:x=-2的距离,可见点P的轨迹是抛物线.抛物线答案解析反思与感悟 判断点的轨迹是抛物线注意应满足两点
(1)判断动点到定点与到定直线的距离相等.
(2)要特别注意定点不在定直线上.跟踪训练3 已知直线l:x+2y-3=0,点F(2,1),P为平面上一动点,过P作PE⊥l于E,PE=PF,则点P的轨迹为________.
解析 ∵点F(2,1)不在直线l上,且PE=PF,
∴点P的轨迹为抛物线.抛物线答案解析达标检测1.动点M到定点 的距离之和是2,则动点M的轨迹是______.
解析 ∵MA+MB=2>1=AB,
∴点M的轨迹是椭圆.椭圆答案12345解析123452.已知两点F1(-5,0),F2(5,0),到它们的距离的差的绝对值是6的点M的轨迹是________.
解析 ∵| MF1-MF2|=6
解析 由题意知,动圆圆心到直线x=-1的距离与到定点(1,0)的距离相等,由抛物线定义可得圆心的轨迹为抛物线.12345抛物线5.如图,已知圆A:(x+3)2+y2=100,圆A内有一定点
B(3,0).动圆P过B点且与圆A内切,设动圆P的半径为r,
试判断圆心P的轨迹.
解 由题意知A(-3,0),
PA=10-r,PB=r,
则PA+PB=10>AB=6,
满足椭圆的定义,
故点P的轨迹是以A,B两点为焦点的椭圆.解答123451.在椭圆定义中,常数>F1F2不可忽视,若常数
3.在抛物线定义中F?l.若F∈l,则点的轨迹是经过点F且垂直于l的直线.
