2018_2019高中数学第2章圆锥曲线与方程2.2.2第1课时椭圆的几何性质课件苏教版选修1_1(44张PPT)
文档属性
| 名称 | 2018_2019高中数学第2章圆锥曲线与方程2.2.2第1课时椭圆的几何性质课件苏教版选修1_1(44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-24 00:00:00 | ||
图片预览










文档简介
课件44张PPT。第1课时 椭圆的几何性质第2章 2.2.2 椭圆的几何性质学习目标1.根据椭圆的方程研究曲线的几何性质,并正确地画出它的图形.
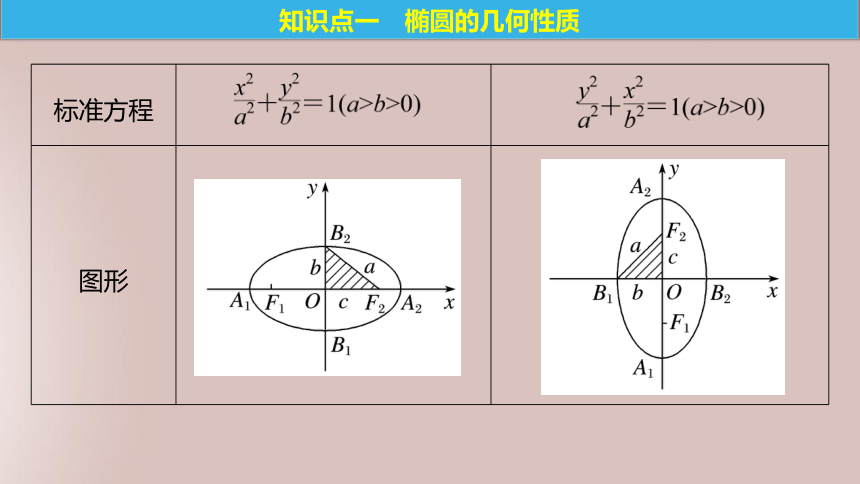
2.根据几何条件求出曲线方程,并利用曲线的方程研究它的性质、图形.问题导学达标检测题型探究内容索引问题导学知识点一 椭圆的几何性质F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)|x|≤a,|y|≤b|x|≤b,|y|≤ax轴、y轴和原点(±a,0),(0,±b)(0,±a),(±b,0)2a2b思考 观察不同的椭圆可见它们的扁平程度不一样,哪些量影响其扁平程度?怎样刻画?
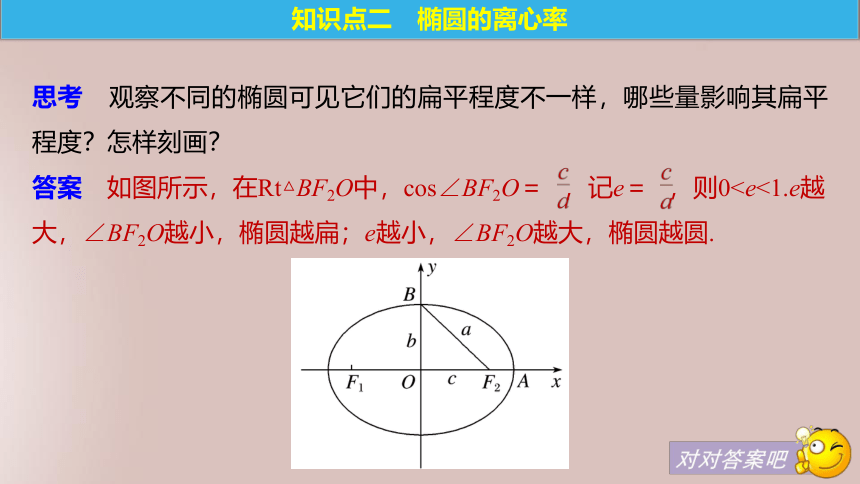
答案 如图所示,在Rt△BF2O中,cos∠BF2O= ,记e= ,则0(2)性质:离心率e的取值范围是 ,当e越接近于1,椭圆越 ,当e越接近于 ,椭圆就越接近于圆.离心率扁(0,1)01.椭圆的顶点是椭圆与坐标轴的交点.( )
2.椭圆上的点到焦点的距离的最小值为a-c.( )
3.椭圆的离心率e越接近于1,椭圆越扁.( )
4.椭圆 (a>b>0)的短轴长等于b.( )[思考辨析 判断正误]××√√题型探究类型一 由椭圆方程研究其几何性质解答顶点坐标为(±4,0),(0,±1).画出第一象限部分的图象,最后利用对称性作出二、三、四象限的图象.画图:先作出直线x=±4,y=±1围成的矩形框,然后在第一象限描点反思与感悟 解决此类问题的方法是将所给方程先化为标准形式,然后根据方程判断出椭圆的焦点在哪个坐标轴上,再利用a,b,c之间的关系和定义,求椭圆的基本量.解答跟踪训练1 求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.四个顶点坐标分别是A1(-4,0),A2(4,0),B1(0,-3)和B2(0,3).类型二 求椭圆的离心率命题角度1 与焦点三角形有关的求离心率问题
例2 椭圆 (a>b>0)的两焦点为F1,F2,以F1F2为边作正三角形,
若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为________.答案解析解析 方法一 如图,
∵△DF1F2为正三角形,N为DF2的中点,
∴F1N⊥F2N.
∵NF2=c,则由椭圆的定义可知,NF1+NF2=2a,方法二 注意到在焦点三角形NF1F2中 ,∠NF1F2=30°,∠NF2F1=60°,∠F1NF2=90°.
则由离心率的公式和正弦定理,得答案解析因为△F2PF1是底角为30°的等腰三角形,则有F1F2=F2P.
因为∠PF1F2=30°,
所以∠PF2D=60°,∠DPF2=30°.命题角度2 构建a,c的齐次式,求椭圆的离心率(或其取值范围)
例3 (1)设椭圆C: (a>b>0)的左、右焦点分别为F1,F2,过F2 作x轴的垂线与椭圆C相交于A,B两点,F1B与y轴相交于点D,若AD⊥F1B,
则椭圆C的离心率为____.答案解析(2)若椭圆 (a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2为
椭圆的两个焦点),则椭圆的离心率e的取值范围为________.答案解析由题意知,以F1F2为直径的圆至少与椭圆有一个公共点,则c≥b,即c2≥b2,
所以c2≥a2-c2,反思与感悟 若a,c的值不可求,则可根据条件建立a,b,c的关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程或不等式,再将方程或不等式两边同除以a的最高次幂,得到关于e的方程或不等式,即可求得e的值或取值范围.答案解析解析 设F0为椭圆的左焦点,连结F0A,F0B,
则四边形AFBF0为平行四边形.
∵AF+BF=4,
∴AF+AF0=4,∴a=2.类型三 利用几何性质求椭圆的标准方程解答解 ∵所求椭圆的方程为标准方程,
又椭圆过点(3,0),∴点(3,0)为椭圆的一个顶点.
①当椭圆的焦点在x轴上时,(3,0)为右顶点,则a=3.②当椭圆的焦点在y轴上时,(3,0)为右顶点,则b=3.∴a2=3b2=27,解答由椭圆的对称性知,B1F=B2F.
又B1F⊥B2F,
∴△B1FB2为等腰直角三角形,
∴OB2=OF,即b=c.反思与感悟 此类问题应由所给的几何性质充分找出a,b,c所应满足的关系式,进而求出a,b.在求解时,需注意当焦点所在位置不确定时,应分类讨论.解答跟踪训练4 根据下列条件,求中心在原点,对称轴在坐标轴上的椭圆方程.
(1)长轴长是短轴长的2倍,且过点(2,-6);解答(2)焦点在x轴上,一个焦点与短轴的两端点连线互相垂直,且半焦距为6.达标检测答案12345解析123452.若椭圆的长轴长是短轴长的2倍,且焦距为2,则此椭圆的标准方程为
____________________.答案解析解析 由题意可知a=2b,c=1,3.已知椭圆以两条坐标轴为对称轴,一个顶点是(0,13),另一个顶点是(-10,0),则焦点坐标为__________.12345答案解析答案解析4.已知点(m,n)在椭圆8x2+3y2=24上,则2m+4的取值范围为__________________.1234512345答案解析1.已知椭圆的方程讨论性质时,若不是标准形式,应先化成标准形式.
2.根据椭圆的几何性质,可以求椭圆的标准方程,其基本思路是“先定型,再定量”,常用的方法是待定系数法.在椭圆的基本量中,能确定类型的量有焦点、顶点,而不能确定类型的量有长轴长、短轴长、离心率e、焦距.
3.求椭圆的离心率要注意函数与方程的思想、数形结合思想的应用.规律与方法
2.根据几何条件求出曲线方程,并利用曲线的方程研究它的性质、图形.问题导学达标检测题型探究内容索引问题导学知识点一 椭圆的几何性质F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)|x|≤a,|y|≤b|x|≤b,|y|≤ax轴、y轴和原点(±a,0),(0,±b)(0,±a),(±b,0)2a2b思考 观察不同的椭圆可见它们的扁平程度不一样,哪些量影响其扁平程度?怎样刻画?
答案 如图所示,在Rt△BF2O中,cos∠BF2O= ,记e= ,则0
2.椭圆上的点到焦点的距离的最小值为a-c.( )
3.椭圆的离心率e越接近于1,椭圆越扁.( )
4.椭圆 (a>b>0)的短轴长等于b.( )[思考辨析 判断正误]××√√题型探究类型一 由椭圆方程研究其几何性质解答顶点坐标为(±4,0),(0,±1).画出第一象限部分的图象,最后利用对称性作出二、三、四象限的图象.画图:先作出直线x=±4,y=±1围成的矩形框,然后在第一象限描点反思与感悟 解决此类问题的方法是将所给方程先化为标准形式,然后根据方程判断出椭圆的焦点在哪个坐标轴上,再利用a,b,c之间的关系和定义,求椭圆的基本量.解答跟踪训练1 求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.四个顶点坐标分别是A1(-4,0),A2(4,0),B1(0,-3)和B2(0,3).类型二 求椭圆的离心率命题角度1 与焦点三角形有关的求离心率问题
例2 椭圆 (a>b>0)的两焦点为F1,F2,以F1F2为边作正三角形,
若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为________.答案解析解析 方法一 如图,
∵△DF1F2为正三角形,N为DF2的中点,
∴F1N⊥F2N.
∵NF2=c,则由椭圆的定义可知,NF1+NF2=2a,方法二 注意到在焦点三角形NF1F2中 ,∠NF1F2=30°,∠NF2F1=60°,∠F1NF2=90°.
则由离心率的公式和正弦定理,得答案解析因为△F2PF1是底角为30°的等腰三角形,则有F1F2=F2P.
因为∠PF1F2=30°,
所以∠PF2D=60°,∠DPF2=30°.命题角度2 构建a,c的齐次式,求椭圆的离心率(或其取值范围)
例3 (1)设椭圆C: (a>b>0)的左、右焦点分别为F1,F2,过F2 作x轴的垂线与椭圆C相交于A,B两点,F1B与y轴相交于点D,若AD⊥F1B,
则椭圆C的离心率为____.答案解析(2)若椭圆 (a>b>0)上存在一点M,使得∠F1MF2=90°(F1,F2为
椭圆的两个焦点),则椭圆的离心率e的取值范围为________.答案解析由题意知,以F1F2为直径的圆至少与椭圆有一个公共点,则c≥b,即c2≥b2,
所以c2≥a2-c2,反思与感悟 若a,c的值不可求,则可根据条件建立a,b,c的关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程或不等式,再将方程或不等式两边同除以a的最高次幂,得到关于e的方程或不等式,即可求得e的值或取值范围.答案解析解析 设F0为椭圆的左焦点,连结F0A,F0B,
则四边形AFBF0为平行四边形.
∵AF+BF=4,
∴AF+AF0=4,∴a=2.类型三 利用几何性质求椭圆的标准方程解答解 ∵所求椭圆的方程为标准方程,
又椭圆过点(3,0),∴点(3,0)为椭圆的一个顶点.
①当椭圆的焦点在x轴上时,(3,0)为右顶点,则a=3.②当椭圆的焦点在y轴上时,(3,0)为右顶点,则b=3.∴a2=3b2=27,解答由椭圆的对称性知,B1F=B2F.
又B1F⊥B2F,
∴△B1FB2为等腰直角三角形,
∴OB2=OF,即b=c.反思与感悟 此类问题应由所给的几何性质充分找出a,b,c所应满足的关系式,进而求出a,b.在求解时,需注意当焦点所在位置不确定时,应分类讨论.解答跟踪训练4 根据下列条件,求中心在原点,对称轴在坐标轴上的椭圆方程.
(1)长轴长是短轴长的2倍,且过点(2,-6);解答(2)焦点在x轴上,一个焦点与短轴的两端点连线互相垂直,且半焦距为6.达标检测答案12345解析123452.若椭圆的长轴长是短轴长的2倍,且焦距为2,则此椭圆的标准方程为
____________________.答案解析解析 由题意可知a=2b,c=1,3.已知椭圆以两条坐标轴为对称轴,一个顶点是(0,13),另一个顶点是(-10,0),则焦点坐标为__________.12345答案解析答案解析4.已知点(m,n)在椭圆8x2+3y2=24上,则2m+4的取值范围为__________________.1234512345答案解析1.已知椭圆的方程讨论性质时,若不是标准形式,应先化成标准形式.
2.根据椭圆的几何性质,可以求椭圆的标准方程,其基本思路是“先定型,再定量”,常用的方法是待定系数法.在椭圆的基本量中,能确定类型的量有焦点、顶点,而不能确定类型的量有长轴长、短轴长、离心率e、焦距.
3.求椭圆的离心率要注意函数与方程的思想、数形结合思想的应用.规律与方法
