2018_2019高中数学第2章圆锥曲线与方程2.2.2第2课时椭圆的几何性质及应用课件苏教版选修1_1(50张PPT)
文档属性
| 名称 | 2018_2019高中数学第2章圆锥曲线与方程2.2.2第2课时椭圆的几何性质及应用课件苏教版选修1_1(50张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-24 09:00:08 | ||
图片预览











文档简介
课件50张PPT。第2课时 椭圆的几何性质及应用第2章 2.2.2 椭圆的几何性质学习目标1.进一步巩固椭圆的简单几何性质.
2.掌握直线与椭圆位置关系等相关知识.问题导学达标检测题型探究内容索引问题导学知识点一 点与椭圆的位置关系思考1 直线与椭圆有几种位置关系?
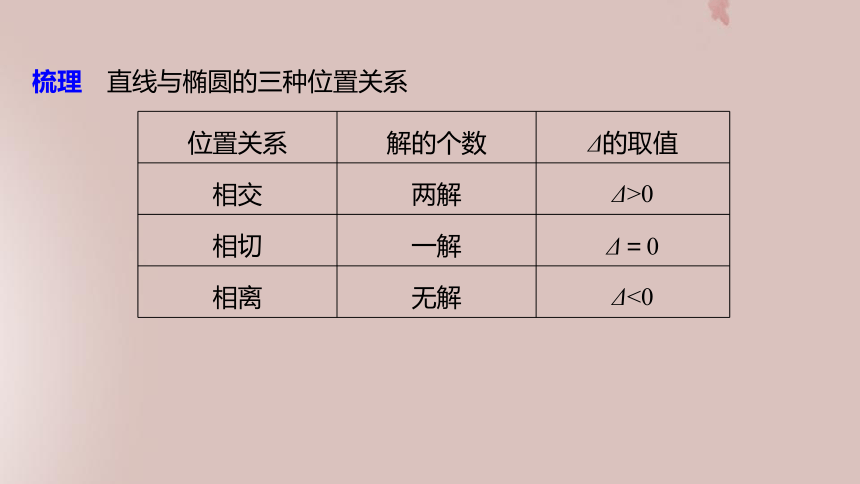
答案 有三种位置关系,分别有相交、相切、相离.知识点二 直线与椭圆的位置关系梳理 直线与椭圆的三种位置关系思考 若直线与椭圆相交,如何求相交弦弦长?
答案 有两种方法:一种方法是联立直线方程与椭圆方程求出交点坐标,利用两点间距离公式可求得;另一种方法是利用弦长公式可求得.知识点三 直线与椭圆的相交弦(直线与椭圆的交点为A(x1,y1),B(x2,y2),k为直线的斜率).
其中,x1+x2,x1x2或y1+y2,y1y2的值,可通过由直线方程与椭圆方程联立,消去y或x后得到关于x或y的一元二次方程,由一元二次方程的根与系数的关系而得到.[思考辨析 判断正误]××√题型探究类型一 直线与椭圆的位置关系解答命题角度1 直线与椭圆位置关系的判定
例1 当m取何值时,直线l:y=x+m与椭圆9x2+16y2=144.
(1)无公共点;得25x2+32mx+16m2-144=0,
Δ=(32m)2-100(16m2-144)
=576(-m2+25).
由Δ<0,解得m<-5或m>5.解答(2)有且仅有一个公共点;
解 由Δ=0,解得m=±5.
(3)有两个公共点.
解 由Δ>0,解得-5Δ=9m2-16(m2-7)=0,即m2=16,得m=±4,反思与感悟 此类题将求最小距离问题转化为直线与椭圆的位置关系问题.解此类问题的常规解法是直线方程与椭圆方程联立,消去y或x得到关于x或y的一元二次方程,则(1)直线与椭圆相交?Δ>0;(2)直线与椭圆相切?Δ=0;(3)直线与椭圆相离?Δ<0.所以判定直线与椭圆的位置关系,方程及其判别式是最基本的工具.解答跟踪训练2 已知椭圆x2+8y2=8,在椭圆上求一点P,使P到直线l:x-y+4=0的距离最短,并求出最短距离.解 设与直线x-y+4=0平行且与椭圆相切的直线为x-y+a=0.得9y2-2ay+a2-8=0,
Δ=4a2-36(a2-8)=0,
解得a=3或a=-3.
∴与直线l距离较近的切线方程为x-y+3=0,类型二 弦长及中点问题解答若设A(x1,y1),B(x2,y2),则x1+x2=0,x1x2=-18.解答(2)当P点恰好为线段AB的中点时,求l的方程.解 方法一 当直线l的斜率不存在时,不合题意.
所以直线l的斜率存在.
设l的斜率为k,则其方程为y-2=k(x-4).消去y得(1+4k2)x2-(32k2-16k)x+(64k2-64k-20)=0.由于AB的中点恰好为P(4,2),由于P(4,2)是AB的中点,∴x1+x2=8,y1+y2=4,反思与感悟 处理直线与椭圆相交的关系问题的通法是通过解直线与椭圆构成的方程.利用根与系数的关系或中点坐标公式解决,涉及弦的中点,还可使用点差法:设出弦的两端点坐标,代入椭圆方程,两式相减即得弦的中点与斜率的关系.解答解 方法一 设A(x1,y1),B(x2,y2),代入椭圆方程并作差,
得a(x1+x2)(x1-x2)+b(y1+y2)(y1-y2)=0. ①∵直线x+y-1=0的斜率为k=-1,联立ax2+by2=1与x+y-1=0,消去y,可得(a+b)x2-2bx+b-1=0.且由已知得x1,x2是方程(a+b)x2-2bx+b-1=0的两根,且直线AB的斜率为k=-1.类型三 椭圆中的最值(或范围)问题解答反思与感悟 解析几何中的综合性问题很多,而且可与很多知识联系在一起出题,例如不等式、三角函数、平面向量以及函数的最值问题等.解决这类问题需要正确地应用转化思想、函数与方程思想和数形结合思想.其中应用比较多的是利用方程根与系数的关系构造等式或函数关系式,这其中要注意利用根的判别式来确定参数的限制条件.解答解 设点A的坐标为(x1,b),点B的坐标为(x2,b).达标检测答案12345解析(1,3)∪(3,+∞)∵Δ>0,∴m>1或m<0.
又∵m>0且m≠3,∴m>1且m≠3.12345答案解析13.椭圆 的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|的
值为____.答案解析12345解析12345答案4.过点P(-1,1)的直线交椭圆 于A,B两点,若线段AB的中点恰为点P,则AB所在的直线方程为____________.x-2y+3=0解析 设A(x1,y1),B(x2,y2),∴AB所在的直线方程为x-2y+3=0.12345解答解 设直线l与椭圆的交点为M(x1,y1),N(x2,y2).12345化简得k4+k2-2=0,
所以k2=1,即k=±1.
所以所求直线l的方程是y=x+1或y=-x+1.123451.直线与椭圆相交弦长的有关问题
(1)当弦的两端点的坐标易求时,可直接求出交点坐标,再用两点间距离公式求弦长.规律与方法(3)如果直线方程涉及斜率,要注意斜率不存在的情况.2.解决椭圆中点弦问题的二种方法
(1)根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用一元二次方程根与系数的关系以及中点坐标公式解决.
(2)点差法:利用端点在曲线上,坐标满足方程,将端点坐标分别代入椭圆方程,然后作差,构造出中点坐标和斜率的关系.
2.掌握直线与椭圆位置关系等相关知识.问题导学达标检测题型探究内容索引问题导学知识点一 点与椭圆的位置关系思考1 直线与椭圆有几种位置关系?
答案 有三种位置关系,分别有相交、相切、相离.知识点二 直线与椭圆的位置关系梳理 直线与椭圆的三种位置关系思考 若直线与椭圆相交,如何求相交弦弦长?
答案 有两种方法:一种方法是联立直线方程与椭圆方程求出交点坐标,利用两点间距离公式可求得;另一种方法是利用弦长公式可求得.知识点三 直线与椭圆的相交弦(直线与椭圆的交点为A(x1,y1),B(x2,y2),k为直线的斜率).
其中,x1+x2,x1x2或y1+y2,y1y2的值,可通过由直线方程与椭圆方程联立,消去y或x后得到关于x或y的一元二次方程,由一元二次方程的根与系数的关系而得到.[思考辨析 判断正误]××√题型探究类型一 直线与椭圆的位置关系解答命题角度1 直线与椭圆位置关系的判定
例1 当m取何值时,直线l:y=x+m与椭圆9x2+16y2=144.
(1)无公共点;得25x2+32mx+16m2-144=0,
Δ=(32m)2-100(16m2-144)
=576(-m2+25).
由Δ<0,解得m<-5或m>5.解答(2)有且仅有一个公共点;
解 由Δ=0,解得m=±5.
(3)有两个公共点.
解 由Δ>0,解得-5
Δ=4a2-36(a2-8)=0,
解得a=3或a=-3.
∴与直线l距离较近的切线方程为x-y+3=0,类型二 弦长及中点问题解答若设A(x1,y1),B(x2,y2),则x1+x2=0,x1x2=-18.解答(2)当P点恰好为线段AB的中点时,求l的方程.解 方法一 当直线l的斜率不存在时,不合题意.
所以直线l的斜率存在.
设l的斜率为k,则其方程为y-2=k(x-4).消去y得(1+4k2)x2-(32k2-16k)x+(64k2-64k-20)=0.由于AB的中点恰好为P(4,2),由于P(4,2)是AB的中点,∴x1+x2=8,y1+y2=4,反思与感悟 处理直线与椭圆相交的关系问题的通法是通过解直线与椭圆构成的方程.利用根与系数的关系或中点坐标公式解决,涉及弦的中点,还可使用点差法:设出弦的两端点坐标,代入椭圆方程,两式相减即得弦的中点与斜率的关系.解答解 方法一 设A(x1,y1),B(x2,y2),代入椭圆方程并作差,
得a(x1+x2)(x1-x2)+b(y1+y2)(y1-y2)=0. ①∵直线x+y-1=0的斜率为k=-1,联立ax2+by2=1与x+y-1=0,消去y,可得(a+b)x2-2bx+b-1=0.且由已知得x1,x2是方程(a+b)x2-2bx+b-1=0的两根,且直线AB的斜率为k=-1.类型三 椭圆中的最值(或范围)问题解答反思与感悟 解析几何中的综合性问题很多,而且可与很多知识联系在一起出题,例如不等式、三角函数、平面向量以及函数的最值问题等.解决这类问题需要正确地应用转化思想、函数与方程思想和数形结合思想.其中应用比较多的是利用方程根与系数的关系构造等式或函数关系式,这其中要注意利用根的判别式来确定参数的限制条件.解答解 设点A的坐标为(x1,b),点B的坐标为(x2,b).达标检测答案12345解析(1,3)∪(3,+∞)∵Δ>0,∴m>1或m<0.
又∵m>0且m≠3,∴m>1且m≠3.12345答案解析13.椭圆 的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|的
值为____.答案解析12345解析12345答案4.过点P(-1,1)的直线交椭圆 于A,B两点,若线段AB的中点恰为点P,则AB所在的直线方程为____________.x-2y+3=0解析 设A(x1,y1),B(x2,y2),∴AB所在的直线方程为x-2y+3=0.12345解答解 设直线l与椭圆的交点为M(x1,y1),N(x2,y2).12345化简得k4+k2-2=0,
所以k2=1,即k=±1.
所以所求直线l的方程是y=x+1或y=-x+1.123451.直线与椭圆相交弦长的有关问题
(1)当弦的两端点的坐标易求时,可直接求出交点坐标,再用两点间距离公式求弦长.规律与方法(3)如果直线方程涉及斜率,要注意斜率不存在的情况.2.解决椭圆中点弦问题的二种方法
(1)根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用一元二次方程根与系数的关系以及中点坐标公式解决.
(2)点差法:利用端点在曲线上,坐标满足方程,将端点坐标分别代入椭圆方程,然后作差,构造出中点坐标和斜率的关系.
