2018_2019高中数学第3章三角恒等变换3.2第2课时二倍角的三角函数的应用课件苏教版必修4(29张PPT)
文档属性
| 名称 | 2018_2019高中数学第3章三角恒等变换3.2第2课时二倍角的三角函数的应用课件苏教版必修4(29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-24 10:42:56 | ||
图片预览








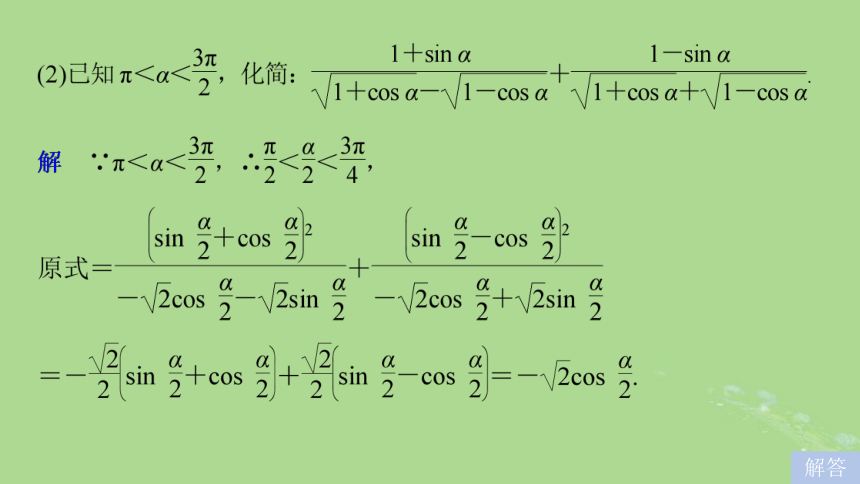
文档简介
课件29张PPT。第2课时 二倍角的三角函数的应用第3章 §3.2 二倍角的三角函数学习目标
1.进一步熟练掌握二倍角公式的特征及正用、逆用.
2.掌握二倍角公式的变形即降幂公式的特征.
3.会用二倍角公式进行三角函数的一些简单的恒等变换.问题导学达标检测题型探究内容索引问题导学知识点 降幂公式思考 答案降幂公式梳理题型探究类型一 化简求值解答解答解答∴等式成立.证明类型二 与三角函数性质有关的问题解答(1)求函数f(x)的最小正周期;(2)求使函数f(x)取得最大值的x的集合.解答(1)为了研究函数的性质,往往要充分利用三角变换公式转化为正弦型(余弦型)函数,这是解决问题的前提.
(2)充分运用两角和(差)、二倍角公式、辅助角转换公式消除差异,减少角的种类和函数式的项数,为讨论函数性质提供了保障.跟踪训练2 已知函数f(x)=sin2x-
(1)求f(x)的最小正周期;解答解答类型三 三角函数在实际问题中的应用解答例3 点P在直径AB=1的半圆上移动,过P作圆的切线PT且PT=1,∠PAB=α,问α为何值时,四边形ABTP面积最大?解 如图所示,∵AB为直径,
∴∠APB=90°,AB=1,PA=cos α,PB=sin α.
又PT切圆于P点,∠TPB=∠PAB=α,
作BC⊥PT于点C.
∴S四边形ABTP=S△PAB+S△TPB利用三角函数知识解决实际问题,关键是目标函数的构建,自变量常常选取一个恰当的角度,要注意结合实际问题确定自变量的范围.跟踪训练3 如图,已知OPQ是半径为1,圆心角为 的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.解答解 在直角三角形OBC中,OB=cos α,BC=sin α.设矩形ABCD的面积为S,则达标检测12345答案解析12345答案解析3.函数y=1+4cos2x的单调增区间是 .12345答案解析解析 y=1+4cos2x=2cos 2x+3,
由-π+2kπ≤2x≤2kπ,k∈Z,
得- +kπ≤x≤kπ,k∈Z,答案解析∴tan α=2,12345答案解析123452.解决有关的化简、求值、证明时注意二倍角公式的综合运用.
3.对于三角函数在实际问题中的应用,其求解策略为引入恰当的辅助角,建立有关辅助角的三角函数表达式,并利用和、差、倍角公式进行化简整理,由于引入辅助角的恰当与否直接影响该题的计算量,故求解时多注意分析题设,恰当引入.
1.进一步熟练掌握二倍角公式的特征及正用、逆用.
2.掌握二倍角公式的变形即降幂公式的特征.
3.会用二倍角公式进行三角函数的一些简单的恒等变换.问题导学达标检测题型探究内容索引问题导学知识点 降幂公式思考 答案降幂公式梳理题型探究类型一 化简求值解答解答解答∴等式成立.证明类型二 与三角函数性质有关的问题解答(1)求函数f(x)的最小正周期;(2)求使函数f(x)取得最大值的x的集合.解答(1)为了研究函数的性质,往往要充分利用三角变换公式转化为正弦型(余弦型)函数,这是解决问题的前提.
(2)充分运用两角和(差)、二倍角公式、辅助角转换公式消除差异,减少角的种类和函数式的项数,为讨论函数性质提供了保障.跟踪训练2 已知函数f(x)=sin2x-
(1)求f(x)的最小正周期;解答解答类型三 三角函数在实际问题中的应用解答例3 点P在直径AB=1的半圆上移动,过P作圆的切线PT且PT=1,∠PAB=α,问α为何值时,四边形ABTP面积最大?解 如图所示,∵AB为直径,
∴∠APB=90°,AB=1,PA=cos α,PB=sin α.
又PT切圆于P点,∠TPB=∠PAB=α,
作BC⊥PT于点C.
∴S四边形ABTP=S△PAB+S△TPB利用三角函数知识解决实际问题,关键是目标函数的构建,自变量常常选取一个恰当的角度,要注意结合实际问题确定自变量的范围.跟踪训练3 如图,已知OPQ是半径为1,圆心角为 的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.解答解 在直角三角形OBC中,OB=cos α,BC=sin α.设矩形ABCD的面积为S,则达标检测12345答案解析12345答案解析3.函数y=1+4cos2x的单调增区间是 .12345答案解析解析 y=1+4cos2x=2cos 2x+3,
由-π+2kπ≤2x≤2kπ,k∈Z,
得- +kπ≤x≤kπ,k∈Z,答案解析∴tan α=2,12345答案解析123452.解决有关的化简、求值、证明时注意二倍角公式的综合运用.
3.对于三角函数在实际问题中的应用,其求解策略为引入恰当的辅助角,建立有关辅助角的三角函数表达式,并利用和、差、倍角公式进行化简整理,由于引入辅助角的恰当与否直接影响该题的计算量,故求解时多注意分析题设,恰当引入.
