2018_2019高中数学第3章三角恒等变换3.3几个三角恒等式课件苏教版必修4(39张PPT)
文档属性
| 名称 | 2018_2019高中数学第3章三角恒等变换3.3几个三角恒等式课件苏教版必修4(39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-24 10:43:48 | ||
图片预览






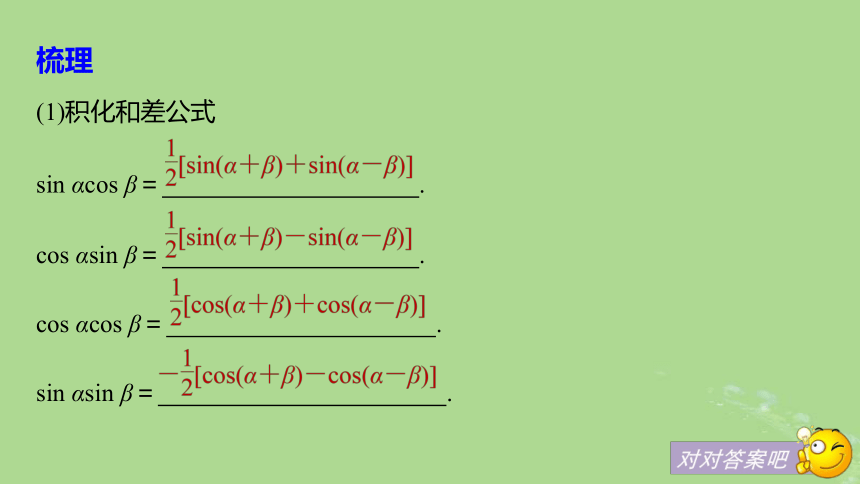


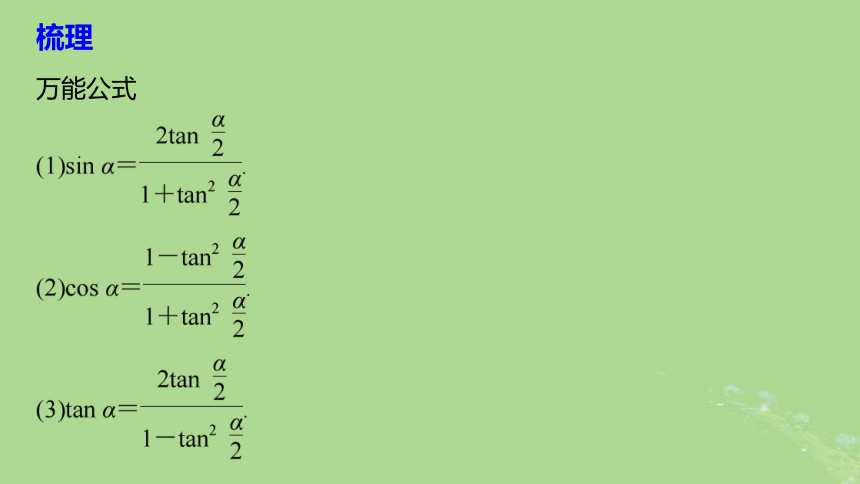


文档简介
课件39张PPT。§3.3 几个三角恒等式第3章 三角恒等变换学习目标
1.理解积化和差、和差化积、万能公式的推导过程.
2.掌握积化和差、和差化积、万能公式的结构特征.
3.能利用所学三角公式进行三角恒等变换.问题导学达标检测题型探究内容索引问题导学知识点一 积化和差与和差化积公式思考1 答案如何用sin(α+β),sin(α-β)表示sin αcos β和cos αsin β?∴sin(α+β)+sin(α-β)=2sin αcos β,
即sin αcos β= [sin(α+β)+sin(α-β)].
同理得cos αsin β= [sin(α+β)-sin(α-β)].思考2 答案若α+β=θ,α-β=φ,则如何用θ,φ表示α,β?(1)积化和差公式
sin αcos β= .
cos αsin β= .
cos αcos β= .
sin αsin β= .梳理(2)和差化积公式
sin α+sin β= .
sin α-sin β= .
cos α+cos β= .
cos α-cos β= .知识点二 万能代换公式思考 答案结合前面所学倍角公式,能否用 表示sin α?万能公式梳理知识点三 半角公式思考1 答案我们知道倍角公式中,“倍角是相对的”,那么对余弦的二倍角公式,若用 替换α,结果怎样?思考2 答案根据上述结果,试用sin α,cos α表示思考3 答案利用tan α= 和倍角公式又能得到 与sin α,cos α怎样的关系?半角公式梳理[思考辨析 判断正误]答案√×题型探究类型一 积化和差与和差化积公式解答命题角度1 积化和差公式的应用
例1 求下列各式的值.
(1)sin 37.5°cos 7.5°;解答(2)sin 20°·sin 40°·sin 80°;解 sin 20°·sin 40°·sin 80°解答(3)sin 20°cos 70°+sin 10°sin 50°.解 sin 20°cos 70°+sin 10°sin 50°反思与感悟在运用积化和差公式时,如果形式为异名函数积时,化得的结果应用sin(α+β)与sin(α-β)的和或差;如果形式为同名函数积时,化得的结果应用cos(α+β)与cos(α-β)的和或差.解答跟踪训练1 化简:4sin(60°-θ)·sin θ·sin(60°+θ).解 原式=-2sin θ·[cos 120°-cos(-2θ)]=sin θ+sin 3θ-sin θ=sin 3θ.解答命题角度2 和差化积公式的应用反思与感悟和差化积公式对于三角函数式的求值、化简及三角函数式的恒等变形有着重要的作用,应用时要注意只有系数的绝对值相同的同名函数的和与差才能直接运用推论化成积的形式,如果是一正弦与一余弦的和或差,可先用诱导公式化成同名函数后,再运用推论化成积的形式.解答跟踪训练2 求sin220°+cos250°+sin 20°cos 50°的值.方法二 原式=(sin 20°+cos 50°)2-sin 20°·cos 50°类型二 利用万能公式化简求值解 ∵180°<θ<270°,解答∴tan θ=2.解答反思与感悟(1)万能公式是三角函数中的重要变形公式,“倍角”的正弦、余弦、正切都可以表示为“单角”的正切的有理式的形式.
(2)万能公式左右两边的角的取值范围不同,在解三角函数方程时,要避免漏解.sin 2θ-2cos2θ=sin 2θ-cos 2θ-1解答类型三 三角恒等式的证明∴左边=右边,∴原等式成立.证明反思与感悟证明三角恒等式的实质是消除等式两边的差异,有目的地化繁为简、左右归一或变更论证.对恒等式的证明,应遵循化繁为简的原则,从左边推到右边或从右边推到左边,也可以用左右归一,变更论证等方法.常用定义法、化弦法、化切法、拆项拆角法、“1”的代换法、公式变形法,要熟练掌握基本公式,善于从中选择巧妙简捷的方法.∴原等式成立.证明达标检测1234答案解析1234答案解析答案解析212341234解答规律与方法1.本节重点学习了积化和差公式、和差化积公式及万能公式等,一定要清楚这些公式的形式特征.同时要理解公式间的关系,立足于公式推导过程中记忆公式.
2.三角恒等式的证明类型
(1)绝对恒等式:证明绝对恒等式要根据等式两边的特征,化繁为简,左右归一,通过三角恒等变换,使等式的两边化异为同.
(2)条件恒等式:条件恒等式的证明要认真观察,比较已知条件与求证等式之间的联系,选择适当的途径,常用代入法、消元法、两头凑法.
1.理解积化和差、和差化积、万能公式的推导过程.
2.掌握积化和差、和差化积、万能公式的结构特征.
3.能利用所学三角公式进行三角恒等变换.问题导学达标检测题型探究内容索引问题导学知识点一 积化和差与和差化积公式思考1 答案如何用sin(α+β),sin(α-β)表示sin αcos β和cos αsin β?∴sin(α+β)+sin(α-β)=2sin αcos β,
即sin αcos β= [sin(α+β)+sin(α-β)].
同理得cos αsin β= [sin(α+β)-sin(α-β)].思考2 答案若α+β=θ,α-β=φ,则如何用θ,φ表示α,β?(1)积化和差公式
sin αcos β= .
cos αsin β= .
cos αcos β= .
sin αsin β= .梳理(2)和差化积公式
sin α+sin β= .
sin α-sin β= .
cos α+cos β= .
cos α-cos β= .知识点二 万能代换公式思考 答案结合前面所学倍角公式,能否用 表示sin α?万能公式梳理知识点三 半角公式思考1 答案我们知道倍角公式中,“倍角是相对的”,那么对余弦的二倍角公式,若用 替换α,结果怎样?思考2 答案根据上述结果,试用sin α,cos α表示思考3 答案利用tan α= 和倍角公式又能得到 与sin α,cos α怎样的关系?半角公式梳理[思考辨析 判断正误]答案√×题型探究类型一 积化和差与和差化积公式解答命题角度1 积化和差公式的应用
例1 求下列各式的值.
(1)sin 37.5°cos 7.5°;解答(2)sin 20°·sin 40°·sin 80°;解 sin 20°·sin 40°·sin 80°解答(3)sin 20°cos 70°+sin 10°sin 50°.解 sin 20°cos 70°+sin 10°sin 50°反思与感悟在运用积化和差公式时,如果形式为异名函数积时,化得的结果应用sin(α+β)与sin(α-β)的和或差;如果形式为同名函数积时,化得的结果应用cos(α+β)与cos(α-β)的和或差.解答跟踪训练1 化简:4sin(60°-θ)·sin θ·sin(60°+θ).解 原式=-2sin θ·[cos 120°-cos(-2θ)]=sin θ+sin 3θ-sin θ=sin 3θ.解答命题角度2 和差化积公式的应用反思与感悟和差化积公式对于三角函数式的求值、化简及三角函数式的恒等变形有着重要的作用,应用时要注意只有系数的绝对值相同的同名函数的和与差才能直接运用推论化成积的形式,如果是一正弦与一余弦的和或差,可先用诱导公式化成同名函数后,再运用推论化成积的形式.解答跟踪训练2 求sin220°+cos250°+sin 20°cos 50°的值.方法二 原式=(sin 20°+cos 50°)2-sin 20°·cos 50°类型二 利用万能公式化简求值解 ∵180°<θ<270°,解答∴tan θ=2.解答反思与感悟(1)万能公式是三角函数中的重要变形公式,“倍角”的正弦、余弦、正切都可以表示为“单角”的正切的有理式的形式.
(2)万能公式左右两边的角的取值范围不同,在解三角函数方程时,要避免漏解.sin 2θ-2cos2θ=sin 2θ-cos 2θ-1解答类型三 三角恒等式的证明∴左边=右边,∴原等式成立.证明反思与感悟证明三角恒等式的实质是消除等式两边的差异,有目的地化繁为简、左右归一或变更论证.对恒等式的证明,应遵循化繁为简的原则,从左边推到右边或从右边推到左边,也可以用左右归一,变更论证等方法.常用定义法、化弦法、化切法、拆项拆角法、“1”的代换法、公式变形法,要熟练掌握基本公式,善于从中选择巧妙简捷的方法.∴原等式成立.证明达标检测1234答案解析1234答案解析答案解析212341234解答规律与方法1.本节重点学习了积化和差公式、和差化积公式及万能公式等,一定要清楚这些公式的形式特征.同时要理解公式间的关系,立足于公式推导过程中记忆公式.
2.三角恒等式的证明类型
(1)绝对恒等式:证明绝对恒等式要根据等式两边的特征,化繁为简,左右归一,通过三角恒等变换,使等式的两边化异为同.
(2)条件恒等式:条件恒等式的证明要认真观察,比较已知条件与求证等式之间的联系,选择适当的途径,常用代入法、消元法、两头凑法.
