2018_2019高中数学第二章数列2.1第2课时数列的递推公式与通项公式课件苏教版必修5(34张PPT)
文档属性
| 名称 | 2018_2019高中数学第二章数列2.1第2课时数列的递推公式与通项公式课件苏教版必修5(34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-24 10:46:00 | ||
图片预览







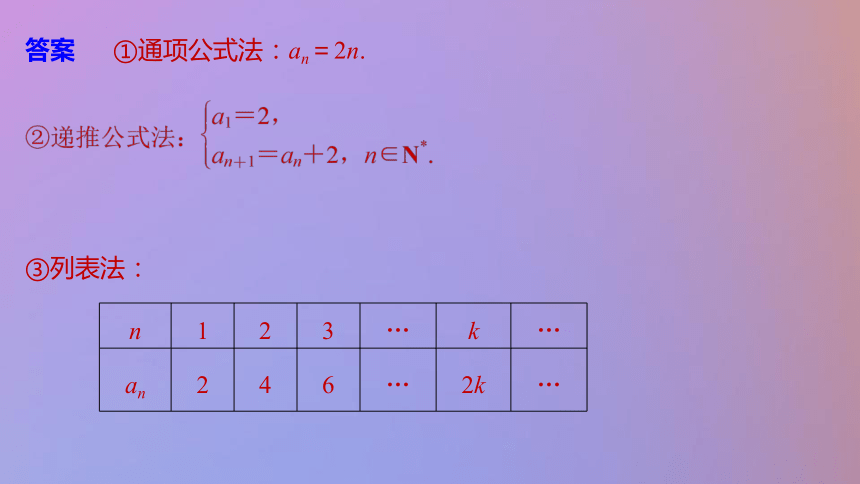




文档简介
课件34张PPT。第2课时 数列的递推公式与通项公式第2章 §2.1 数 列学习目标
1.理解数列的几种表示方法,能从函数的观点研究数列.
2.理解递推公式的含义,能根据递推公式求出数列的前几项.
3.会用累加法、累乘法由递推公式求通项公式.问题导学达标检测题型探究内容索引问题导学知识点一 递推公式思考 数列1,2,4,8,…的第n项an与第n+1项an+1有什么关系?答案 an+1=2an梳理 如果已知数列的第1项(或前几项),且从第 项(或某一项)开始的任一项 与它的前一项 (或前几项)(n≥2)间的关系可以用一个公式表示,那么这个公式叫做这个数列的递推公式.二anan-1特别提醒:(1)与所有的数列不一定都有通项公式一样,并不是所有的数列都有递推公式.
(2)递推公式通过赋值逐项求出数列的项,直至求出数列的任何一项和所需的项.知识点二 数列的表示方法思考 以数列2,4,6,8,10,12,…为例,你能用几种方法表示这个数列?答案 ①通项公式法:an=2n.③列表法:④图象法:梳理 数列的表示方法有通项公式法、图象法、列表法、递推公式法.[思考辨析 判断正误]
1.利用an+1=2an,n∈N*可以确定数列{an}.( )
2.有些数列难以用通项公式和递推公式表示,但可以用列表法轻松解决.( )
3.递推公式是表示数列的一种方法.( )×√√题型探究例1 图中的三角形图案称为谢宾斯基三角形,在四个三角形图案中,着色的小三角形的个数依次构成一个数列的前4项,请写出这个数列的递推公式和一个通项公式,并在直角坐标系中画出它的图象.类型一 数列的表示法解答解 如题图,这四个三角形图案中着色的小三角形第(2)个是第(1)个的3倍,第(3)个是第(2)个的3倍,故有递推公式a1=1,an+1=3an,n∈N*,个数依次为1,3,9,27.则所求数列的前4项都是3的指数幂,指数为序号减1.
所以,这个数列的一个通项公式是an=3n-1.在直角坐标系中的图象为一些孤立的点(如图所示).反思与感悟 求数列的递推公式注重观察数列项与项的关系,求通项公式注重观察项与序号的关系,图象法则一如既往地直观.跟踪训练1 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数.比如,他们将石子摆成如图所示的三角形点阵,就将其所对应石子的个数称为三角形数,则第n个三角形数比第n-1(n≥2,n∈N*)个三角形数多___个石子.n答案解析解析 a2-a1=2,a3-a2=3,…,∴an-an-1=n.命题角度1 由递推公式求前若干项解答类型二 数列的递推公式解答引申探究∴{an}是周期为4的数列,
∴a2 018=a4×504+2=a2=-3.反思与感悟 递推公式反映的是相邻两项(或n项)之间的关系.对于通项公式,已知n的值即可得到相应的项;而递推公式则要已知首项(或前几项),才可依次求得其他的项.若项数很大,则应考虑数列是否有规律性.解答解 a1=1,a2=2,a3=1,a4=-1,a5=-2,
a6=-1,a7=1,a8=2,….
发现:an+6=an,数列{an}具有周期性,周期T=6.
证明如下:∵an+2=an+1-an,
∴an+3=an+2-an+1=(an+1-an)-an+1=-an.
∴an+6=-an+3=-(-an)=an.
∴数列{an}是周期数列,且T=6.
∴a2 018=a336×6+2=a2=2.跟踪训练2 已知数列{an}中,a1=1,a2=2,an+2=an+1-an,试写出a3,a4,a5,a6,a7,a8,你发现数列{an}具有怎样的规律?你能否求出该数列中的第2 018项?命题角度2 由递推公式求通项
例3 (1)对于任意数列{an},等式:a1+(a2-a1)+(a3-a2)+…+(an-an-1)=an(n≥2,n∈N*)都成立.试根据这一结论,完成问题:已知数列{an}满足:a1=1,an+1-an=2,求通项an;解答解 当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+ =2(n-1)+1=2n-1.
a1=1也符合上式,
所以数列{an}的通项公式是an=2n-1.解答a1=1也符合上式,解答…,又当n=1时,a1=-1,也符合上式.∴(a2-a1)+(a3-a2)+(a4-a3)+…+(an-an-1)达标检测1.数列1,3,6,10,15,…中an=an-1+____(n∈N*且n>1).答案解析1234n解析 由已知得a2-a1=2,a3-a2=3,a4-a3=4,
a5-a4=5,…,an+1-an=n+1,n∈N*.答案解析1234解析 ∵an+1-an=-1.
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=2+
=2+(-1)×(n-1)=3-n.2.已知数列{an}满足a1=2,an+1-an+1=0(n∈N*),则此数列的通项an=_______.3-n答案解析1234an=2n+1,n∈N*3.用火柴棒按下图的方法搭三角形:
按图示的规律搭下去,则所用火柴棒数an与所搭三角形的个数n之间的关系式可以是_________________.解析 a1=3,a2=3+2=5,a3=3+2+2=7,
a4=3+2+2+2=9,…,∴an=2n+1,n∈N*.1234解析 ∵x1=1,∴x2=- ,∴x3=1,
∴数列{xn}的周期为2,∴x2 018=x2=- .答案解析1.{an}与an是不同的两种表示,{an}表示数列a1,a2,…,an,…,是数列的一种简记形式.而an只表示数列{an}的第n项,an与{an}是“个体”与“整体”的从属关系.
2.数列的表示方法:(1)图象法;(2)列表法;(3)通项公式法;(4)递推公式法.
3.通项公式和递推公式的区别:通项公式直接反映an和n之间的关系,即an是n的函数,知道任意一个具体的n值,就可以求出该项的值an;而递推公式则是间接反映数列的式子,它是数列任意两个(或多个)相邻项之间的推导关系,不能由n直接得出an.规律与方法
1.理解数列的几种表示方法,能从函数的观点研究数列.
2.理解递推公式的含义,能根据递推公式求出数列的前几项.
3.会用累加法、累乘法由递推公式求通项公式.问题导学达标检测题型探究内容索引问题导学知识点一 递推公式思考 数列1,2,4,8,…的第n项an与第n+1项an+1有什么关系?答案 an+1=2an梳理 如果已知数列的第1项(或前几项),且从第 项(或某一项)开始的任一项 与它的前一项 (或前几项)(n≥2)间的关系可以用一个公式表示,那么这个公式叫做这个数列的递推公式.二anan-1特别提醒:(1)与所有的数列不一定都有通项公式一样,并不是所有的数列都有递推公式.
(2)递推公式通过赋值逐项求出数列的项,直至求出数列的任何一项和所需的项.知识点二 数列的表示方法思考 以数列2,4,6,8,10,12,…为例,你能用几种方法表示这个数列?答案 ①通项公式法:an=2n.③列表法:④图象法:梳理 数列的表示方法有通项公式法、图象法、列表法、递推公式法.[思考辨析 判断正误]
1.利用an+1=2an,n∈N*可以确定数列{an}.( )
2.有些数列难以用通项公式和递推公式表示,但可以用列表法轻松解决.( )
3.递推公式是表示数列的一种方法.( )×√√题型探究例1 图中的三角形图案称为谢宾斯基三角形,在四个三角形图案中,着色的小三角形的个数依次构成一个数列的前4项,请写出这个数列的递推公式和一个通项公式,并在直角坐标系中画出它的图象.类型一 数列的表示法解答解 如题图,这四个三角形图案中着色的小三角形第(2)个是第(1)个的3倍,第(3)个是第(2)个的3倍,故有递推公式a1=1,an+1=3an,n∈N*,个数依次为1,3,9,27.则所求数列的前4项都是3的指数幂,指数为序号减1.
所以,这个数列的一个通项公式是an=3n-1.在直角坐标系中的图象为一些孤立的点(如图所示).反思与感悟 求数列的递推公式注重观察数列项与项的关系,求通项公式注重观察项与序号的关系,图象法则一如既往地直观.跟踪训练1 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数.比如,他们将石子摆成如图所示的三角形点阵,就将其所对应石子的个数称为三角形数,则第n个三角形数比第n-1(n≥2,n∈N*)个三角形数多___个石子.n答案解析解析 a2-a1=2,a3-a2=3,…,∴an-an-1=n.命题角度1 由递推公式求前若干项解答类型二 数列的递推公式解答引申探究∴{an}是周期为4的数列,
∴a2 018=a4×504+2=a2=-3.反思与感悟 递推公式反映的是相邻两项(或n项)之间的关系.对于通项公式,已知n的值即可得到相应的项;而递推公式则要已知首项(或前几项),才可依次求得其他的项.若项数很大,则应考虑数列是否有规律性.解答解 a1=1,a2=2,a3=1,a4=-1,a5=-2,
a6=-1,a7=1,a8=2,….
发现:an+6=an,数列{an}具有周期性,周期T=6.
证明如下:∵an+2=an+1-an,
∴an+3=an+2-an+1=(an+1-an)-an+1=-an.
∴an+6=-an+3=-(-an)=an.
∴数列{an}是周期数列,且T=6.
∴a2 018=a336×6+2=a2=2.跟踪训练2 已知数列{an}中,a1=1,a2=2,an+2=an+1-an,试写出a3,a4,a5,a6,a7,a8,你发现数列{an}具有怎样的规律?你能否求出该数列中的第2 018项?命题角度2 由递推公式求通项
例3 (1)对于任意数列{an},等式:a1+(a2-a1)+(a3-a2)+…+(an-an-1)=an(n≥2,n∈N*)都成立.试根据这一结论,完成问题:已知数列{an}满足:a1=1,an+1-an=2,求通项an;解答解 当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+ =2(n-1)+1=2n-1.
a1=1也符合上式,
所以数列{an}的通项公式是an=2n-1.解答a1=1也符合上式,解答…,又当n=1时,a1=-1,也符合上式.∴(a2-a1)+(a3-a2)+(a4-a3)+…+(an-an-1)达标检测1.数列1,3,6,10,15,…中an=an-1+____(n∈N*且n>1).答案解析1234n解析 由已知得a2-a1=2,a3-a2=3,a4-a3=4,
a5-a4=5,…,an+1-an=n+1,n∈N*.答案解析1234解析 ∵an+1-an=-1.
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=2+
=2+(-1)×(n-1)=3-n.2.已知数列{an}满足a1=2,an+1-an+1=0(n∈N*),则此数列的通项an=_______.3-n答案解析1234an=2n+1,n∈N*3.用火柴棒按下图的方法搭三角形:
按图示的规律搭下去,则所用火柴棒数an与所搭三角形的个数n之间的关系式可以是_________________.解析 a1=3,a2=3+2=5,a3=3+2+2=7,
a4=3+2+2+2=9,…,∴an=2n+1,n∈N*.1234解析 ∵x1=1,∴x2=- ,∴x3=1,
∴数列{xn}的周期为2,∴x2 018=x2=- .答案解析1.{an}与an是不同的两种表示,{an}表示数列a1,a2,…,an,…,是数列的一种简记形式.而an只表示数列{an}的第n项,an与{an}是“个体”与“整体”的从属关系.
2.数列的表示方法:(1)图象法;(2)列表法;(3)通项公式法;(4)递推公式法.
3.通项公式和递推公式的区别:通项公式直接反映an和n之间的关系,即an是n的函数,知道任意一个具体的n值,就可以求出该项的值an;而递推公式则是间接反映数列的式子,它是数列任意两个(或多个)相邻项之间的推导关系,不能由n直接得出an.规律与方法
