2018_2019高中数学第2章圆锥曲线与方程2.4.1抛物线的标准方程课件苏教版选修1_1(43张)
文档属性
| 名称 | 2018_2019高中数学第2章圆锥曲线与方程2.4.1抛物线的标准方程课件苏教版选修1_1(43张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-25 10:56:33 | ||
图片预览





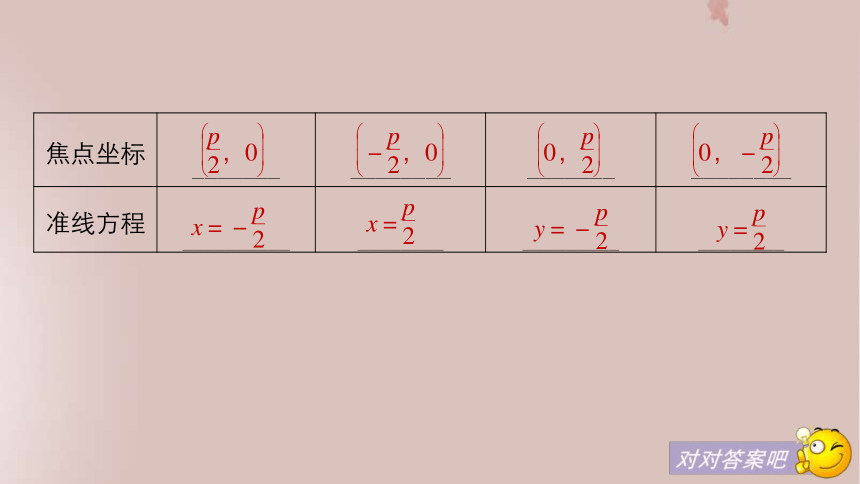





文档简介
课件43张PPT。2.4.1 抛物线的标准方程第2章 §2.4 抛物线学习目标1.掌握抛物线的定义及焦点、准线的概念.
2.掌握抛物线的标准方程及其推导过程.
3.明确抛物线标准方程中p的几何意义,能解决简单的求抛物线标准方程的问题.问题导学达标检测题型探究内容索引问题导学知识点 抛物线的标准方程思考1 在抛物线方程中p有何意义?抛物线的开口方向由什么决定?
答案 p是抛物线的焦点到准线的距离,抛物线方程中一次项决定开口方向.
思考2 已知抛物线的标准方程,怎样确定抛物线的焦点位置和开口方向?
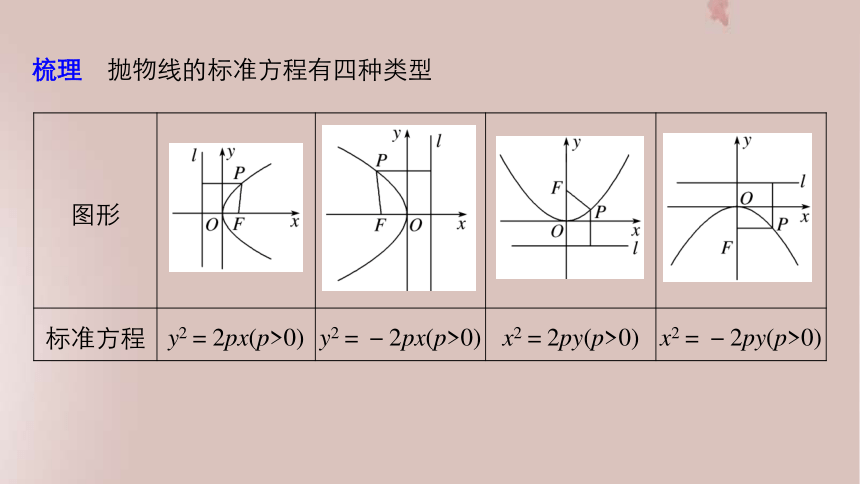
答案 一次项变量为x(或y),则焦点在x轴(或y轴)上.若系数为正,则焦点在正半轴上;若系数为负,则焦点在负半轴上.焦点确定,开口方向也随之确定.梳理 抛物线的标准方程有四种类型1.抛物线y2=2x(p>0)的焦点坐标为(1,0).( )
2.到定点的距离与到定直线的距离相等的点的轨迹是抛物线.( )
3.抛物线的方程都是y关于x的二次函数.( )
4.方程x2=2py是表示开口向上的抛物线.( )[思考辨析 判断正误]××××题型探究类型一 求抛物线的标准方程解答例1 分别根据下列条件求抛物线的标准方程:
(1)已知抛物线的焦点坐标是F(0,-2);解 因为抛物线的焦点在y轴的负半轴上,所以所求抛物线的标准方程为x2=-8y.解答解 因为抛物线的准线平行于x轴,且在x轴上面,解答(3)焦点在x轴负半轴上,焦点到准线的距离是5;解 由焦点到准线的距离为5知,p=5.
又焦点在x轴负半轴上,
所以所求抛物线的标准方程为y2=-10x.解答(4)过点A(2,3).解 由题意知,抛物线方程可设为y2=mx(m≠0)或x2=ny(n≠0).将点A(2,3)的坐标代入,反思与感悟 求抛物线方程,通常用待定系数法,若能确定抛物线的焦点位置,则可设出抛物线的标准方程,求出p值即可.若抛物线的焦点位置不确定,则要分情况讨论.焦点在x轴上的抛物线方程可设为y2=ax(a≠0),焦点在y轴上的抛物线方程可设为x2=ay(a≠0).解答跟踪训练1 分别求满足下列条件的抛物线的标准方程:
(1)过点(3,-4);解 方法一 ∵点(3,-4)在第四象限,
∴设抛物线的标准方程为y2=2px(p>0)或x2=-2p1y(p1>0).
把点(3,-4)分别代入y2=2px和x2=-2p1y,
得(-4)2=2p·3,32=-2p1·(-4),方法二 ∵点(3,-4)在第四象限,
∴设抛物线的方程为y2=ax(a≠0)或x2=by(b≠0).解答(2)焦点在直线x+3y+15=0上,且焦点在坐标轴上;
解 令x=0,得y=-5;令y=0,得x=-15,
∴抛物线的焦点坐标为(0,-5)或(-15,0).
∴所求抛物线的标准方程为x2=-20y或y2=-60x.解答(3)焦点到准线的距离为 .类型二 求抛物线的焦点坐标及准线方程例2 已知抛物线的方程如下,求其焦点坐标和准线方程:
(1)y2=-6x;
解 由方程y2=-6x知,抛物线开口向左,解答(2)3x2+5y=0;解答(3)y=4x2;解答(4)y2=a2x(a≠0).
解 由方程y2=a2x(a≠0)知,抛物线开口向右,解答引申探究
若将本例(4)中条件改为y=ax2(a≠0),结果又如何?解答反思与感悟 如果已知抛物线的标准方程,求它的焦点坐标、准线方程时,首先要判断抛物线的对称轴和开口方向.一次项的变量若为x(或y),则x轴(或y轴)是抛物线的对称轴,一次项系数的符号决定开口方向.跟踪训练2 若抛物线y2=2px的焦点坐标为(1,0),则p=___,准线方程为________.答案解析2x=-1类型三 抛物线定义的应用解答其方程应为y2=2px(p>0)的形式,故点M的轨迹方程为y2=2x(x≠0).反思与感悟 满足抛物线的定义,可直接利用定义写出轨迹方程,避免了繁琐的化简.跟踪训练3 平面上动点P到定点F(1,0)的距离比点P到y轴的距离大1,求动点P的轨迹方程.
解 由题意知,动点P到定点F(1,0)的距离比到y轴的距离大1.
由于点F(1,0)到y轴的距离为1,故当x<0时,直线y=0上的点适合条件;
当x≥0时,原命题等价于点P到点F(1,0)与到直线x=-1的距离相等,
故点P的轨迹是以F为焦点,x=-1为准线的抛物线,方程为y2=4x.解答解答命题角度2 利用抛物线定义求最值
例4 设P是抛物线y2=4x上的一个动点,F为抛物线的焦点.
(1)求点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值;解 如图,易知抛物线的焦点坐标为F(1,0),
准线方程是x=-1.
由抛物线的定义知,
点P到直线x=-1的距离等于点P到焦点F的距离,
于是问题转化为在曲线上求一点P,
使点P到点A(-1,1)的距离与点P到F(1,0)的距离之和最小.
显然,连结AF,
AF与抛物线的交点即为点P,故最小值为=
即点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值为解答(2)若点B的坐标为(3,2).求PB+PF的最小值. 过点B作BQ垂直于准线,
垂足为点Q,交抛物线于点P1,连结P1F.
此时,由抛物线定义知,P1Q=P1F.
所以PB+PF≥P1B+P1Q=BQ=3+1=4,
即PB+PF的最小值为4.反思与感悟 解决最值问题:在抛物线中求解与焦点有关的两点间距离和的最小值时,往往用抛物线的定义进行转化,即化折线为直线来解决最值问题.跟踪训练4 已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是___.
解析 由题意知,直线l2:x=-1为抛物线y2=4x的准线.
由抛物线的定义知,点P到l2的距离等于点P到抛物线的焦点F(1,0)的距离,
故所求最值可转化为在抛物线y2=4x上找一个点P,
使得点P到点F(1,0)和到直线l1的距离之和最小,
最小值为F(1,0)到直线l1:4x-3y+6=0的距离,2答案解析达标检测答案12345解析y=-112345答案解析2.设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是___.
解析 抛物线y2=8x的准线方程为x=-2,则点P到准线的距离是6.
由抛物线的定义可知,点P到抛物线焦点的距离是6.63.根据下列条件写出抛物线的标准方程:
(1)准线方程为x=-1.________.12345答案解析y2=4x又焦点在x轴上,则抛物线的标准方程为y2=4x.(2)焦点在x轴的负半轴上,焦点到准线的距离是2._________.
解析 ∵焦点到准线的距离为p=2,且焦点在x轴的负半轴上,
∴抛物线的标准方程为y2=-4x.y2=-4x答案解析12345123455.若抛物线y2=-2px(p>0)上有一点M,其横坐标为-9,它到焦点的距离为10,求抛物线方程和M点的坐标.解答由题意设点M到准线的距离为MN,故抛物线方程为y2=-4x.
将M(-9,y0)代入抛物线方程,得y0=±6.
∴M点的坐标为(-9,6)或(-9,-6).规律与方法3.对于抛物线上的点,利用定义可以把其到焦点的距离转化为到准线的距离,也可以把其到准线的距离转化为到焦点的距离,因此可以解决有关距离的最值问题.
2.掌握抛物线的标准方程及其推导过程.
3.明确抛物线标准方程中p的几何意义,能解决简单的求抛物线标准方程的问题.问题导学达标检测题型探究内容索引问题导学知识点 抛物线的标准方程思考1 在抛物线方程中p有何意义?抛物线的开口方向由什么决定?
答案 p是抛物线的焦点到准线的距离,抛物线方程中一次项决定开口方向.
思考2 已知抛物线的标准方程,怎样确定抛物线的焦点位置和开口方向?
答案 一次项变量为x(或y),则焦点在x轴(或y轴)上.若系数为正,则焦点在正半轴上;若系数为负,则焦点在负半轴上.焦点确定,开口方向也随之确定.梳理 抛物线的标准方程有四种类型1.抛物线y2=2x(p>0)的焦点坐标为(1,0).( )
2.到定点的距离与到定直线的距离相等的点的轨迹是抛物线.( )
3.抛物线的方程都是y关于x的二次函数.( )
4.方程x2=2py是表示开口向上的抛物线.( )[思考辨析 判断正误]××××题型探究类型一 求抛物线的标准方程解答例1 分别根据下列条件求抛物线的标准方程:
(1)已知抛物线的焦点坐标是F(0,-2);解 因为抛物线的焦点在y轴的负半轴上,所以所求抛物线的标准方程为x2=-8y.解答解 因为抛物线的准线平行于x轴,且在x轴上面,解答(3)焦点在x轴负半轴上,焦点到准线的距离是5;解 由焦点到准线的距离为5知,p=5.
又焦点在x轴负半轴上,
所以所求抛物线的标准方程为y2=-10x.解答(4)过点A(2,3).解 由题意知,抛物线方程可设为y2=mx(m≠0)或x2=ny(n≠0).将点A(2,3)的坐标代入,反思与感悟 求抛物线方程,通常用待定系数法,若能确定抛物线的焦点位置,则可设出抛物线的标准方程,求出p值即可.若抛物线的焦点位置不确定,则要分情况讨论.焦点在x轴上的抛物线方程可设为y2=ax(a≠0),焦点在y轴上的抛物线方程可设为x2=ay(a≠0).解答跟踪训练1 分别求满足下列条件的抛物线的标准方程:
(1)过点(3,-4);解 方法一 ∵点(3,-4)在第四象限,
∴设抛物线的标准方程为y2=2px(p>0)或x2=-2p1y(p1>0).
把点(3,-4)分别代入y2=2px和x2=-2p1y,
得(-4)2=2p·3,32=-2p1·(-4),方法二 ∵点(3,-4)在第四象限,
∴设抛物线的方程为y2=ax(a≠0)或x2=by(b≠0).解答(2)焦点在直线x+3y+15=0上,且焦点在坐标轴上;
解 令x=0,得y=-5;令y=0,得x=-15,
∴抛物线的焦点坐标为(0,-5)或(-15,0).
∴所求抛物线的标准方程为x2=-20y或y2=-60x.解答(3)焦点到准线的距离为 .类型二 求抛物线的焦点坐标及准线方程例2 已知抛物线的方程如下,求其焦点坐标和准线方程:
(1)y2=-6x;
解 由方程y2=-6x知,抛物线开口向左,解答(2)3x2+5y=0;解答(3)y=4x2;解答(4)y2=a2x(a≠0).
解 由方程y2=a2x(a≠0)知,抛物线开口向右,解答引申探究
若将本例(4)中条件改为y=ax2(a≠0),结果又如何?解答反思与感悟 如果已知抛物线的标准方程,求它的焦点坐标、准线方程时,首先要判断抛物线的对称轴和开口方向.一次项的变量若为x(或y),则x轴(或y轴)是抛物线的对称轴,一次项系数的符号决定开口方向.跟踪训练2 若抛物线y2=2px的焦点坐标为(1,0),则p=___,准线方程为________.答案解析2x=-1类型三 抛物线定义的应用解答其方程应为y2=2px(p>0)的形式,故点M的轨迹方程为y2=2x(x≠0).反思与感悟 满足抛物线的定义,可直接利用定义写出轨迹方程,避免了繁琐的化简.跟踪训练3 平面上动点P到定点F(1,0)的距离比点P到y轴的距离大1,求动点P的轨迹方程.
解 由题意知,动点P到定点F(1,0)的距离比到y轴的距离大1.
由于点F(1,0)到y轴的距离为1,故当x<0时,直线y=0上的点适合条件;
当x≥0时,原命题等价于点P到点F(1,0)与到直线x=-1的距离相等,
故点P的轨迹是以F为焦点,x=-1为准线的抛物线,方程为y2=4x.解答解答命题角度2 利用抛物线定义求最值
例4 设P是抛物线y2=4x上的一个动点,F为抛物线的焦点.
(1)求点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值;解 如图,易知抛物线的焦点坐标为F(1,0),
准线方程是x=-1.
由抛物线的定义知,
点P到直线x=-1的距离等于点P到焦点F的距离,
于是问题转化为在曲线上求一点P,
使点P到点A(-1,1)的距离与点P到F(1,0)的距离之和最小.
显然,连结AF,
AF与抛物线的交点即为点P,故最小值为=
即点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值为解答(2)若点B的坐标为(3,2).求PB+PF的最小值. 过点B作BQ垂直于准线,
垂足为点Q,交抛物线于点P1,连结P1F.
此时,由抛物线定义知,P1Q=P1F.
所以PB+PF≥P1B+P1Q=BQ=3+1=4,
即PB+PF的最小值为4.反思与感悟 解决最值问题:在抛物线中求解与焦点有关的两点间距离和的最小值时,往往用抛物线的定义进行转化,即化折线为直线来解决最值问题.跟踪训练4 已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是___.
解析 由题意知,直线l2:x=-1为抛物线y2=4x的准线.
由抛物线的定义知,点P到l2的距离等于点P到抛物线的焦点F(1,0)的距离,
故所求最值可转化为在抛物线y2=4x上找一个点P,
使得点P到点F(1,0)和到直线l1的距离之和最小,
最小值为F(1,0)到直线l1:4x-3y+6=0的距离,2答案解析达标检测答案12345解析y=-112345答案解析2.设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是___.
解析 抛物线y2=8x的准线方程为x=-2,则点P到准线的距离是6.
由抛物线的定义可知,点P到抛物线焦点的距离是6.63.根据下列条件写出抛物线的标准方程:
(1)准线方程为x=-1.________.12345答案解析y2=4x又焦点在x轴上,则抛物线的标准方程为y2=4x.(2)焦点在x轴的负半轴上,焦点到准线的距离是2._________.
解析 ∵焦点到准线的距离为p=2,且焦点在x轴的负半轴上,
∴抛物线的标准方程为y2=-4x.y2=-4x答案解析12345123455.若抛物线y2=-2px(p>0)上有一点M,其横坐标为-9,它到焦点的距离为10,求抛物线方程和M点的坐标.解答由题意设点M到准线的距离为MN,故抛物线方程为y2=-4x.
将M(-9,y0)代入抛物线方程,得y0=±6.
∴M点的坐标为(-9,6)或(-9,-6).规律与方法3.对于抛物线上的点,利用定义可以把其到焦点的距离转化为到准线的距离,也可以把其到准线的距离转化为到焦点的距离,因此可以解决有关距离的最值问题.
