2018_2019高中数学第3章导数及其应用3.1.1平均变化率课件苏教版选修1_1(31张)
文档属性
| 名称 | 2018_2019高中数学第3章导数及其应用3.1.1平均变化率课件苏教版选修1_1(31张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-25 11:02:35 | ||
图片预览











文档简介
课件31张PPT。3.1.1 平均变化率第3章 §3.1 导数的概念学习目标1.通过实例,了解平均变化率的概念,并会求具体函数的平均变化率.
2.了解平均变化率概念的形成过程,会在具体的环境中,说明平均变化率的实际意义.
3.了解平均变化率的正负.问题导学达标检测题型探究内容索引问题导学知识点一 函数的平均变化率思考2 当空气容量从V1增加到V2时,气球的平均膨胀率是多少?Δy=f(x2)-f(x1)知识点二 平均变化率的意义思考 如何用数学反映曲线的“陡峭”程度?
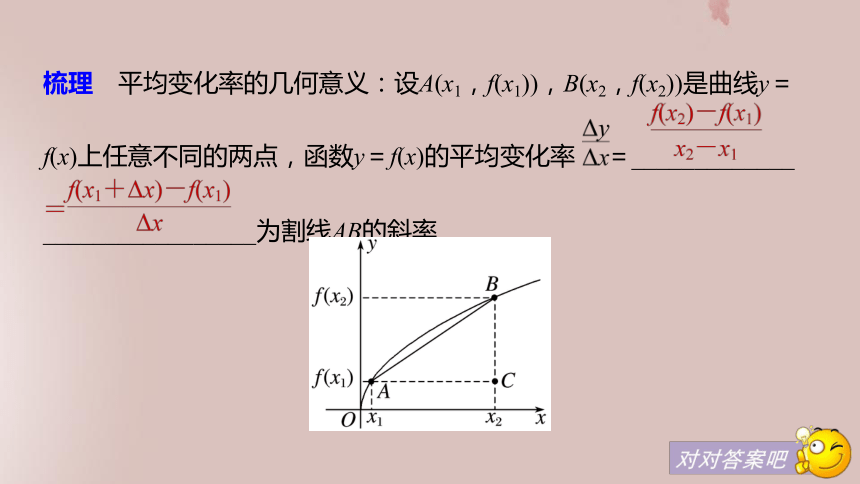
答案 如图,表示A,B之间的曲线和B,C之间的曲线的陡峭程度,可以近似地用直线的斜率来量化.如用比值 近似量化B,C这一段曲线的陡峭程度,并称该比值是曲线在[xB,xC]上的平均变化率.梳理 平均变化率的几何意义:设A(x1,f(x1)),B(x2,f(x2))是曲线y=
f(x)上任意不同的两点,函数y=f(x)的平均变化率 =_____________ _________________为割线AB的斜率.1.函数y=x2+1在[2,3]上的平均变化率是5.( )
2.甲、乙二人销售化妆品,从2014年2月开始的3个月内,甲投入资金5万元,获利4万元,乙投入资金8万元,获利6万元.因此我们认为乙的经营效果较好.( )
3.一次函数任意两点的平均变化率都是相应直线的斜率.( )
4.函数f(x)在A(x1,y1),B(x2,y2)上的平均变化率就是直线AB的斜率.
( )[思考辨析 判断正误]√×√√题型探究类型一 求函数的平均变化率解答解 因为f(x)=2x2+3x-5,
所以Δy=f(x1+Δx)-f(x1)
=2(x1+Δx)2+3(x1+Δx)-5-(2 +3x1-5)
=2[(Δx)2+2x1Δx]+3Δx
=2(Δx)2+(4x1+3)Δx.当x1=4,x2=5时,Δx=1,解答解 当x1=4,x2=4.1时,Δx=0.1,
Δy=2(Δx)2+(4x1+3)Δx=0.02+1.9=1.92.解答由于k1∴Δx=3-(-1)=4,Δy=4-2=2,解答类型二 平均变化率的应用解答例2 在高台跳水运动中,运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+6.5t+10.
(1)求运动员在第一个0.5 s内高度h的平均变化率;解答(2)求高度h在1≤t≤2这段时间内的平均变化率.反思与感悟 (1)结合物理知识可知,在第一个0.5 s内高度h的平均变化率为正值,表示此时运动员在起跳后处于上升过程;在1≤t≤2这段时间内,高度h的平均变化率为负值,表示此时运动员已开始向水面下降.事实上平均变化率的值可正、可负也可以是0.
(2)平均变化率的应用主要有:求某一时间段内的平均速度,物体受热膨胀率,高度(重量)的平均变化率等等.解决这些问题的关键在于找准自变量和因变量.跟踪训练2 某婴儿从出生到第12个月的体重变化如图所示,则从出生到第3个月与从第6个月到第12个月体重的平均变化率分别为______千克/月.1,0.4答案解析达标检测答案12345解析1.一质点运动的方程为S=5-3t2,则在一段时间[1,1+Δt]内相应的平均速度是________.-3Δt-6123452.圆的半径r从0.1变化到0.3时,圆的面积S的平均变化率为______.0.4π答案解析解析 ∵S=πr2,12345答案解析3.如图,函数y=f(x)在A,B两点间的平均变化率为_____.-112345答案解析4.如图,函数y=f(x)在[x1,x2],[x2,x3],[x3,x4]这几个区间内,平均变化率最大的一个区间是_______.[x3,x4]结合图象可以发现函数y=f(x)的平均变化率最大的一个区间是[x3,x4].12345解答5.甲企业用2年时间获利100万元,乙企业投产6个月时间就获利30万元,如何比较和评价甲、乙两企业的生产效益?(设两企业投产前的投资成本都是10万元)1.准确理解平均变化率的意义是求解平均变化率的关键,其实质是函数值增量Δy与自变量取值增量Δx的比值.涉及具体问题,计算Δy很容易出现运算错误,因此,计算时要注意括号的应用,先列式再化简,这是减少错误的有效方法.
2.函数的平均变化率在生产生活中有广泛的应用,如平均速度、平均劳动生产率、面积体积变化率等.解决这类问题的关键是能从实际问题中引出数学模型并列出函数关系式,需注意是相对什么量变化的.规律与方法
2.了解平均变化率概念的形成过程,会在具体的环境中,说明平均变化率的实际意义.
3.了解平均变化率的正负.问题导学达标检测题型探究内容索引问题导学知识点一 函数的平均变化率思考2 当空气容量从V1增加到V2时,气球的平均膨胀率是多少?Δy=f(x2)-f(x1)知识点二 平均变化率的意义思考 如何用数学反映曲线的“陡峭”程度?
答案 如图,表示A,B之间的曲线和B,C之间的曲线的陡峭程度,可以近似地用直线的斜率来量化.如用比值 近似量化B,C这一段曲线的陡峭程度,并称该比值是曲线在[xB,xC]上的平均变化率.梳理 平均变化率的几何意义:设A(x1,f(x1)),B(x2,f(x2))是曲线y=
f(x)上任意不同的两点,函数y=f(x)的平均变化率 =_____________ _________________为割线AB的斜率.1.函数y=x2+1在[2,3]上的平均变化率是5.( )
2.甲、乙二人销售化妆品,从2014年2月开始的3个月内,甲投入资金5万元,获利4万元,乙投入资金8万元,获利6万元.因此我们认为乙的经营效果较好.( )
3.一次函数任意两点的平均变化率都是相应直线的斜率.( )
4.函数f(x)在A(x1,y1),B(x2,y2)上的平均变化率就是直线AB的斜率.
( )[思考辨析 判断正误]√×√√题型探究类型一 求函数的平均变化率解答解 因为f(x)=2x2+3x-5,
所以Δy=f(x1+Δx)-f(x1)
=2(x1+Δx)2+3(x1+Δx)-5-(2 +3x1-5)
=2[(Δx)2+2x1Δx]+3Δx
=2(Δx)2+(4x1+3)Δx.当x1=4,x2=5时,Δx=1,解答解 当x1=4,x2=4.1时,Δx=0.1,
Δy=2(Δx)2+(4x1+3)Δx=0.02+1.9=1.92.解答由于k1
(1)求运动员在第一个0.5 s内高度h的平均变化率;解答(2)求高度h在1≤t≤2这段时间内的平均变化率.反思与感悟 (1)结合物理知识可知,在第一个0.5 s内高度h的平均变化率为正值,表示此时运动员在起跳后处于上升过程;在1≤t≤2这段时间内,高度h的平均变化率为负值,表示此时运动员已开始向水面下降.事实上平均变化率的值可正、可负也可以是0.
(2)平均变化率的应用主要有:求某一时间段内的平均速度,物体受热膨胀率,高度(重量)的平均变化率等等.解决这些问题的关键在于找准自变量和因变量.跟踪训练2 某婴儿从出生到第12个月的体重变化如图所示,则从出生到第3个月与从第6个月到第12个月体重的平均变化率分别为______千克/月.1,0.4答案解析达标检测答案12345解析1.一质点运动的方程为S=5-3t2,则在一段时间[1,1+Δt]内相应的平均速度是________.-3Δt-6123452.圆的半径r从0.1变化到0.3时,圆的面积S的平均变化率为______.0.4π答案解析解析 ∵S=πr2,12345答案解析3.如图,函数y=f(x)在A,B两点间的平均变化率为_____.-112345答案解析4.如图,函数y=f(x)在[x1,x2],[x2,x3],[x3,x4]这几个区间内,平均变化率最大的一个区间是_______.[x3,x4]结合图象可以发现函数y=f(x)的平均变化率最大的一个区间是[x3,x4].12345解答5.甲企业用2年时间获利100万元,乙企业投产6个月时间就获利30万元,如何比较和评价甲、乙两企业的生产效益?(设两企业投产前的投资成本都是10万元)1.准确理解平均变化率的意义是求解平均变化率的关键,其实质是函数值增量Δy与自变量取值增量Δx的比值.涉及具体问题,计算Δy很容易出现运算错误,因此,计算时要注意括号的应用,先列式再化简,这是减少错误的有效方法.
2.函数的平均变化率在生产生活中有广泛的应用,如平均速度、平均劳动生产率、面积体积变化率等.解决这类问题的关键是能从实际问题中引出数学模型并列出函数关系式,需注意是相对什么量变化的.规律与方法
