2018-2019学年江苏省镇江市高一(上)期末数学试卷解析版
文档属性
| 名称 | 2018-2019学年江苏省镇江市高一(上)期末数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 247.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-25 07:53:31 | ||
图片预览



文档简介
2018-2019学年江苏省镇江市高一(上)期末数学试卷
一、选择题(本大题共8小题,每小题5分,共40分.在每小题所给出的四个选项中,只有一项是正确的,请把正确选项前的字母代号填涂在答题卡相应位置上)
1.(5分)与角﹣390°终边相同的最小正角是( )
A.﹣30° B.30° C.60° D.330°
2.(5分)函数f(x)=3x﹣8的零点是( )
A.log38 B.log83 C.(log38,0) D.(log83,0)
3.(5分)要得到函数y=sin(2x+)的图象,只要将函数y=sin2x的图象( )
A.向左平移单位 B.向右平移单位
C.向右平移单位 D.向左平移单位
4.(5分)已知角A,B是△ABC中的两个内角,则“A<B”是“cosA>cosB”的( )条件.
A.充分不必要 B.必要不充分
C.既不充分又不必要 D.充要
5.(5分)已知函数f(x)=2x+x﹣10的零点x0∈(k,k+1),则整数k的值为( )
A.0 B.1 C.2 D.3
6.(5分)一个单摆如图所示,以OA为始边,OB为终边的角与时间t(s)的函数满足:,则单摆完成5次完整摆动所花的时间为( )
A.5 B.10 C. D.5π
7.(5分)已知,若角α的终边经过点P(1,),则f(f(cosα))的值为( )
A. B. C.4 D.﹣4
8.(5分)已知函数,g(x)=lnx,则方程f(x)+|g(x)|=0解的个数为( )
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,每小题5分,共计40分.不需要写出解答过程,请将答案填写在答题卡相应的位置上.)
9.(5分)已知圆心角为60°的扇形,其半径为3,则该扇形的面积为 .
10.(5分)若点P(2,4),Q(3,y0)均在幂函数y=f(x)的图象上,则实数y0= .
11.(5分)已知,则tanx= .
12.(5分)计算:= .
13.(5分)已知函数f(x)=2ksinx+3,若对任意x∈[,]都有f(x)≥0恒成立,则实数k的取值范围为 .
14.(5分)求值:= .
15.(5分)已知,x∈(,π),则cos2x= .
16.(5分)某辆汽车以xkm/h的速度在高速公路上匀速行驶(考虑到高速公路行车安全,要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为L,其中k为常数.若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.欲使每小时的油耗不超过9L,则速度x的取值范围为 .
三、解答题(本大题共6小题,共计70分.请在答题纸指定区域内作答,解答应写出文字说明,证明过程或演算步骤.)
17.(10分)设全集U=R,集合A={x|lg(x﹣a)>0},B={x|x2﹣3x﹣4<0}.
(1)当a=1时,求集合A∩B;
(2)若A∪B=A,求实数a的取值范围.
18.(12分)已知A,B均为锐角,sinA=,cos(A+B)=.
(1)求cos2A的值;
(2)求sin(A﹣B)的值.
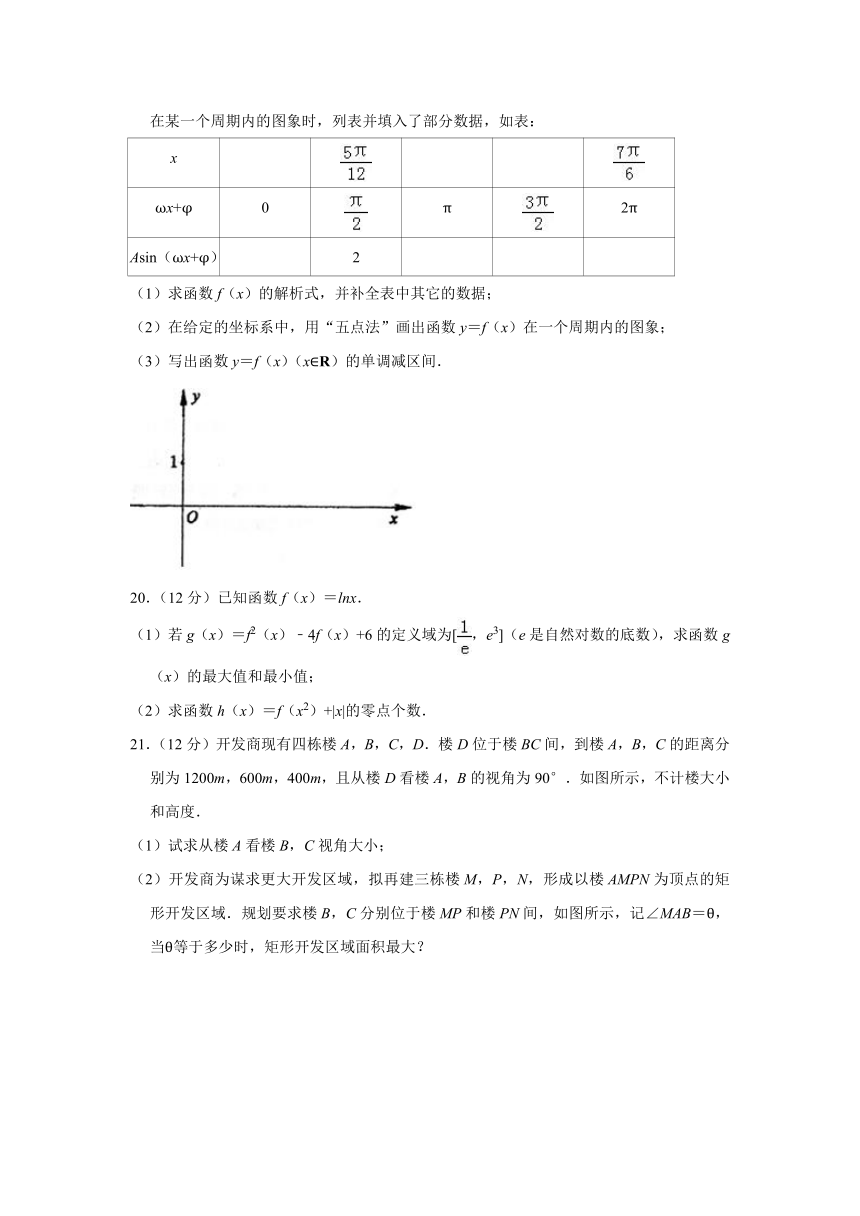
19.(12分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(A>0,ω>0,)在某一个周期内的图象时,列表并填入了部分数据,如表:
x
ωx+φ 0 π 2π
Asin(ωx+φ) 2
(1)求函数f(x)的解析式,并补全表中其它的数据;
(2)在给定的坐标系中,用“五点法”画出函数y=f(x)在一个周期内的图象;
(3)写出函数y=f(x)(x∈R)的单调减区间.
20.(12分)已知函数f(x)=lnx.
(1)若g(x)=f2(x)﹣4f(x)+6的定义域为[,e3](e是自然对数的底数),求函数g(x)的最大值和最小值;
(2)求函数h(x)=f(x2)+|x|的零点个数.
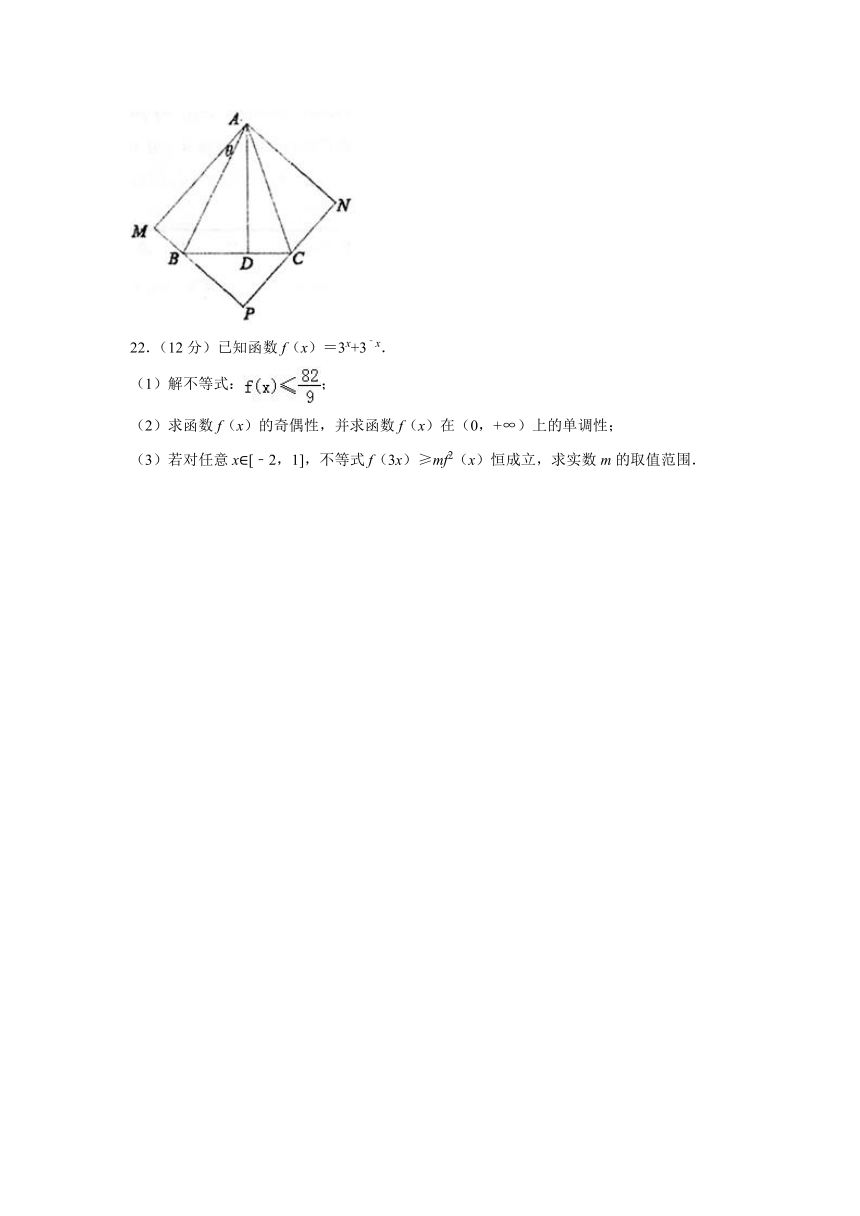
21.(12分)开发商现有四栋楼A,B,C,D.楼D位于楼BC间,到楼A,B,C的距离分别为1200m,600m,400m,且从楼D看楼A,B的视角为90°.如图所示,不计楼大小和高度.
(1)试求从楼A看楼B,C视角大小;
(2)开发商为谋求更大开发区域,拟再建三栋楼M,P,N,形成以楼AMPN为顶点的矩形开发区域.规划要求楼B,C分别位于楼MP和楼PN间,如图所示,记∠MAB=θ,当θ等于多少时,矩形开发区域面积最大?
22.(12分)已知函数f(x)=3x+3﹣x.
(1)解不等式:;
(2)求函数f(x)的奇偶性,并求函数f(x)在(0,+∞)上的单调性;
(3)若对任意x∈[﹣2,1],不等式f(3x)≥mf2(x)恒成立,求实数m的取值范围.
2018-2019学年江苏省镇江市高一(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共8小题,每小题5分,共40分.在每小题所给出的四个选项中,只有一项是正确的,请把正确选项前的字母代号填涂在答题卡相应位置上)
1.【解答】解:﹣390°=﹣2×360°+330°,
即与角﹣390°终边相同的最小正角是330°,
故选:D.
2.【解答】解:解方程3x﹣8=0,解得:x=log38,
故函数f(x)=3x﹣8的零点是log38,
故选:A.
3.【解答】解:由于函数y=sin(2x+)=sin2(x+),
故只要将函数y=sin2x的图象相左平移个单位,即可得到函数y=sin(2x+)的图象,
故选:D.
4.【解答】解:在三角形中,0<A,B<π,
则由cosA>cosB得A<B,
即“A<B”是“cosA>cosB”的充要条件,
故选:D.
5.【解答】解:函数f(x)为增函数,
∵f(2)=22+2﹣10=6﹣10=﹣4<0,
f(3)=32+3﹣10=12﹣10=2>0,
∴f(2)f(3)<0,
即函数在(2,3)内存在一个零点x0,
∵零点x0∈(k,k+1),
∴k=2,
故选:C.
6.【解答】解:∵T==π,即完成一次完整的摆动需时π,
∴单摆完成5次完整摆动需要时间t=5T=5π.
故选:D.
7.【解答】解:∵已知,若角α的终边经过点P(1,),∴cosα==,f(f(cosα))的值.
∴f(cosα)=f()==﹣1,
则f(f(cosα))=f(﹣1)=4﹣1=,
故选:A.
8.【解答】解:由已知有:=,
其图象关于点(3,﹣1)对称,
h(x)=﹣f(x)=其图象关于点(3,1)对称,
方程f(x)+|g(x)|=0解的个数等价于y=h(x)
与y=|g(x)|的图象的交点个数,
由图可知,y=h(x)与y=|g(x)|的图象的交点个数为3,
故选:C.
二、填空题(本大题共8小题,每小题5分,共计40分.不需要写出解答过程,请将答案填写在答题卡相应的位置上.)
9.【解答】解:圆心角为,
则弧长l=3×=π
则扇形的面积S=lr==,
故答案为:
10.【解答】解:∵点P(2,4),Q(3,y0)均在幂函数y=f(x)=xα的图象上,
∴2α=4,解得α=2,∴f(x)=x2,
∴=9.
∴实数y0=9.
故答案为:9.
11.【解答】解:∵
∴=2
∴tanθ=3
故答案为:3
12.【解答】解:=cos(﹣)+sin=cos+sin=,
故答案为:.
13.【解答】解:∵x∈[,],
∴sinx∈[﹣,],
∴2sinx∈[﹣1,1],
当k>0时,f(x)∈[﹣k+3,k+3],
∵对任意x∈[,]都有f(x)≥0恒成立,
∴﹣k+3≥0,即0<k≤3
当k<0时,f(x)∈[k+3,﹣k+3],
∵对任意x∈[,]都有f(x)≥0恒成立,
∴k+3≥0,即﹣3≤k<0,
当k=0时,f(x)=3≥0恒成立,
综上所述实数k的取值范围为[﹣3,3],
故答案为:[﹣3,3]
14.【解答】解:===4?==4,
故答案为:4
15.【解答】解:∵已知,x∈(,π),∴2x∈(π,2π),1+2sinxcosx=,
∴sinxcosx=﹣<0,故sinx﹣cosx==(sinx+cosx)2﹣4sinxcosx=,
∴cos2x=(cosx+sinx)(cosx﹣sinx)=?(﹣)=﹣,
故答案为:﹣.
16.【解答】解:设每小时的油耗(所需要的汽油量)为y,
由题意可得y=,
当x=120时,y=11.5,
∴11.5=(120﹣k+),解得k=100,
∴y=(x﹣100+)
∵每小时的油耗不超过9L,
∴(x﹣100+)≤0,
即x2﹣145x+4500≤0,解得45≤x≤100,
又60≤x≤120,可得60≤x≤100,
每小时的油耗不超过9升,x的取值范围为[60,100],
故答案为:[60,100]
三、解答题(本大题共6小题,共计70分.请在答题纸指定区域内作答,解答应写出文字说明,证明过程或演算步骤.)
17.【解答】解:(1)当a=1时,由于lg(x﹣1)>0=lg1,即x﹣1>1,所以A=(2,+∞)
由于x2﹣3x﹣4<0,即(x+1)(x﹣4)<0,所以B=(﹣1,4)
所以A∩B=(2,4);
(2)因为A∪B=A,所以B?A,
由于A=(a+1,+∞),则a+1≤﹣1,
所以a≤﹣2,所以实数a的取值范围为(﹣∞,﹣2].
18.【解答】解:(1)∵A,B均为锐角,sinA=,cos(A+B)=,∴cos2A=1﹣2sin2A=.
(2)由题意cosA==,sin2A=2sinAcosA=,sin(A+B)==,
∴sin(A﹣B)=sin[2A﹣(A+B)]=sin2A?cos(A+B)﹣cos2A?sin(A+B)=?﹣?=.
19.【解答】解:(1)根据用“五点法”画函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的步骤方法,
由所给的表格可得A=2,ω?+φ=,且ω?+φ=2π,
∴ω=2,φ=﹣,∴f(x)=2sin(2x﹣),
可得表格应为:
x
ωx+φ 0 π 2π
Asin(ωx+φ) 0 2 0 ﹣2 0
(2)根据五点法作图,作出函数的一个周期内的图象,
如图:
(3)根据函数的图象以及周期性可得它的减区间为[kπ+,kπ+],k∈Z.
20.【解答】解:(1)y=g(x)=ln2x﹣4lnx+6的定义域是[,e3],
则设t=lnx∈[﹣1,3],
则y=s(t)=t2﹣4t+6=(t﹣2)2+2在[﹣1,2]递减,在[2,3]递增,
故ymin=s(2)=2,
∵s(﹣1)>s(3),则ymax=s(﹣1)=11;
(2)函数h(x)=f(x2)+|x|=2ln|x|+|x|,x∈(﹣∞,0)∪(0,+∞),
∵h(﹣x)=2ln|﹣x|+|﹣x|=2ln|x|+|x|=h(x),故h(x)是偶函数,
当x>0时,h(x)=2lnx+x在(0,+∞)连续不断,且单调递增,
又h(1)=2ln1+1=1>0,h()=﹣2+<0,
则函数h(x)在(0,+∞)上存在唯一的零点,
由于函数h(x)是偶函数,则函数h(x)在(﹣∞,0)上也存在唯一的零点,
综上,函数h(x)在定义域内零点的个数是2个.
21.【解答】解:(1)因为楼D到楼B、C的距离分别为600m和400m,到楼A的距离为1200m,
所以AD=12百米,BD=6百米,CD=4百米,
因为从楼D看楼A、B的视角为90°,则∠ADB=90°,
则tan∠BAD==,tan∠CAD==,
所以tan∠BAC=tan(∠BAD+∠CAD)===1,
又0<∠BAD+∠CAD<π,即∠BAC∈(0,π),
所以∠BAC=,
则从楼A看楼B,C视角的大小为;
(2)在Rt△ABD和Rt△ACD中,AB==6,
AC==4,
则在Rt△ABM中,AM=ABcosθ=6cosθ,
在Rt△ACN中,AN=ACcos(﹣θ)=4cos(﹣θ),
记矩形开发区AMPN的面积为f(θ),
则f(θ)=AM?AN=4cos(﹣θ)×6cosθ=120cosθcos(﹣θ);
又f(θ)=120cosθ(cosθ+sinθ)=60+60(sin2θ+cos2θ)=60+60sin(2θ+);
当2θ+=时,即θ=时,矩形开发区域AMPN的面积最大.
22.【解答】解:(1)∵函数f(x)≤
∴3x+3﹣x≤,
即9?(3x)2﹣82×3x+9≤0,
即(9?3x﹣1)(3x﹣9)≤0
解得≤3x≤9,
解得﹣2≤x≤2,
故不等式的解集为[﹣2,2].
(2)∵函数f(x)的定义域为R,
∴f(﹣x)=3﹣x+3x=f(x),
∴f(x)为偶函数,
(2)函数f(x)在[0,+∞)上单调递增.
证明如下:在[0,+∞)上任取x1,x2,令x1<x2,
f(x1)﹣f(x2)=+﹣﹣=(﹣)?
∵0≤x1<x2,
∴﹣<0,﹣1>0,
∴f(x1)﹣f(x2)<0,
∴函数f(x)在[0,+∞)上单调递增.
(3)对任意x∈[﹣2,1],不等式f(3x)≥mf2(x)恒成立,即33x+3﹣3x≥m(3x+3﹣x)2,
从而有(3x+3﹣x)(32x+3﹣2x+1)≥m(3x+3﹣x)2恒成立,
∵3x+3﹣x>0,
则等价于32x+3﹣2x+1≥m(3x+3﹣x)恒成立,
令t=3x+3﹣x,则32x+3﹣2x=t2﹣2,
由于f(x)为偶函数,由(2)可知f(x)在(0,+∞)上单调递增,
则函数f(x)在(﹣∞,0)上单调递减,
∵{f(x)|x∈[﹣2,1]}={f(x)|x∈[0,2]},
∴f(0)≤f(x)≤f(2),
∴2≤t≤,
则原不等式等价于t2﹣3≥mt,t∈[2,],
即m≤t﹣在t∈[2,]上恒成立,
设g(t)=t﹣,则g(t)在[2,]上为增函数,
∴g(t)≥g(2)=,
∴m≤
一、选择题(本大题共8小题,每小题5分,共40分.在每小题所给出的四个选项中,只有一项是正确的,请把正确选项前的字母代号填涂在答题卡相应位置上)
1.(5分)与角﹣390°终边相同的最小正角是( )
A.﹣30° B.30° C.60° D.330°
2.(5分)函数f(x)=3x﹣8的零点是( )
A.log38 B.log83 C.(log38,0) D.(log83,0)
3.(5分)要得到函数y=sin(2x+)的图象,只要将函数y=sin2x的图象( )
A.向左平移单位 B.向右平移单位
C.向右平移单位 D.向左平移单位
4.(5分)已知角A,B是△ABC中的两个内角,则“A<B”是“cosA>cosB”的( )条件.
A.充分不必要 B.必要不充分
C.既不充分又不必要 D.充要
5.(5分)已知函数f(x)=2x+x﹣10的零点x0∈(k,k+1),则整数k的值为( )
A.0 B.1 C.2 D.3
6.(5分)一个单摆如图所示,以OA为始边,OB为终边的角与时间t(s)的函数满足:,则单摆完成5次完整摆动所花的时间为( )
A.5 B.10 C. D.5π
7.(5分)已知,若角α的终边经过点P(1,),则f(f(cosα))的值为( )
A. B. C.4 D.﹣4
8.(5分)已知函数,g(x)=lnx,则方程f(x)+|g(x)|=0解的个数为( )
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,每小题5分,共计40分.不需要写出解答过程,请将答案填写在答题卡相应的位置上.)
9.(5分)已知圆心角为60°的扇形,其半径为3,则该扇形的面积为 .
10.(5分)若点P(2,4),Q(3,y0)均在幂函数y=f(x)的图象上,则实数y0= .
11.(5分)已知,则tanx= .
12.(5分)计算:= .
13.(5分)已知函数f(x)=2ksinx+3,若对任意x∈[,]都有f(x)≥0恒成立,则实数k的取值范围为 .
14.(5分)求值:= .
15.(5分)已知,x∈(,π),则cos2x= .
16.(5分)某辆汽车以xkm/h的速度在高速公路上匀速行驶(考虑到高速公路行车安全,要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为L,其中k为常数.若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.欲使每小时的油耗不超过9L,则速度x的取值范围为 .
三、解答题(本大题共6小题,共计70分.请在答题纸指定区域内作答,解答应写出文字说明,证明过程或演算步骤.)
17.(10分)设全集U=R,集合A={x|lg(x﹣a)>0},B={x|x2﹣3x﹣4<0}.
(1)当a=1时,求集合A∩B;
(2)若A∪B=A,求实数a的取值范围.
18.(12分)已知A,B均为锐角,sinA=,cos(A+B)=.
(1)求cos2A的值;
(2)求sin(A﹣B)的值.
19.(12分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(A>0,ω>0,)在某一个周期内的图象时,列表并填入了部分数据,如表:
x
ωx+φ 0 π 2π
Asin(ωx+φ) 2
(1)求函数f(x)的解析式,并补全表中其它的数据;
(2)在给定的坐标系中,用“五点法”画出函数y=f(x)在一个周期内的图象;
(3)写出函数y=f(x)(x∈R)的单调减区间.
20.(12分)已知函数f(x)=lnx.
(1)若g(x)=f2(x)﹣4f(x)+6的定义域为[,e3](e是自然对数的底数),求函数g(x)的最大值和最小值;
(2)求函数h(x)=f(x2)+|x|的零点个数.
21.(12分)开发商现有四栋楼A,B,C,D.楼D位于楼BC间,到楼A,B,C的距离分别为1200m,600m,400m,且从楼D看楼A,B的视角为90°.如图所示,不计楼大小和高度.
(1)试求从楼A看楼B,C视角大小;
(2)开发商为谋求更大开发区域,拟再建三栋楼M,P,N,形成以楼AMPN为顶点的矩形开发区域.规划要求楼B,C分别位于楼MP和楼PN间,如图所示,记∠MAB=θ,当θ等于多少时,矩形开发区域面积最大?
22.(12分)已知函数f(x)=3x+3﹣x.
(1)解不等式:;
(2)求函数f(x)的奇偶性,并求函数f(x)在(0,+∞)上的单调性;
(3)若对任意x∈[﹣2,1],不等式f(3x)≥mf2(x)恒成立,求实数m的取值范围.
2018-2019学年江苏省镇江市高一(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共8小题,每小题5分,共40分.在每小题所给出的四个选项中,只有一项是正确的,请把正确选项前的字母代号填涂在答题卡相应位置上)
1.【解答】解:﹣390°=﹣2×360°+330°,
即与角﹣390°终边相同的最小正角是330°,
故选:D.
2.【解答】解:解方程3x﹣8=0,解得:x=log38,
故函数f(x)=3x﹣8的零点是log38,
故选:A.
3.【解答】解:由于函数y=sin(2x+)=sin2(x+),
故只要将函数y=sin2x的图象相左平移个单位,即可得到函数y=sin(2x+)的图象,
故选:D.
4.【解答】解:在三角形中,0<A,B<π,
则由cosA>cosB得A<B,
即“A<B”是“cosA>cosB”的充要条件,
故选:D.
5.【解答】解:函数f(x)为增函数,
∵f(2)=22+2﹣10=6﹣10=﹣4<0,
f(3)=32+3﹣10=12﹣10=2>0,
∴f(2)f(3)<0,
即函数在(2,3)内存在一个零点x0,
∵零点x0∈(k,k+1),
∴k=2,
故选:C.
6.【解答】解:∵T==π,即完成一次完整的摆动需时π,
∴单摆完成5次完整摆动需要时间t=5T=5π.
故选:D.
7.【解答】解:∵已知,若角α的终边经过点P(1,),∴cosα==,f(f(cosα))的值.
∴f(cosα)=f()==﹣1,
则f(f(cosα))=f(﹣1)=4﹣1=,
故选:A.
8.【解答】解:由已知有:=,
其图象关于点(3,﹣1)对称,
h(x)=﹣f(x)=其图象关于点(3,1)对称,
方程f(x)+|g(x)|=0解的个数等价于y=h(x)
与y=|g(x)|的图象的交点个数,
由图可知,y=h(x)与y=|g(x)|的图象的交点个数为3,
故选:C.
二、填空题(本大题共8小题,每小题5分,共计40分.不需要写出解答过程,请将答案填写在答题卡相应的位置上.)
9.【解答】解:圆心角为,
则弧长l=3×=π
则扇形的面积S=lr==,
故答案为:
10.【解答】解:∵点P(2,4),Q(3,y0)均在幂函数y=f(x)=xα的图象上,
∴2α=4,解得α=2,∴f(x)=x2,
∴=9.
∴实数y0=9.
故答案为:9.
11.【解答】解:∵
∴=2
∴tanθ=3
故答案为:3
12.【解答】解:=cos(﹣)+sin=cos+sin=,
故答案为:.
13.【解答】解:∵x∈[,],
∴sinx∈[﹣,],
∴2sinx∈[﹣1,1],
当k>0时,f(x)∈[﹣k+3,k+3],
∵对任意x∈[,]都有f(x)≥0恒成立,
∴﹣k+3≥0,即0<k≤3
当k<0时,f(x)∈[k+3,﹣k+3],
∵对任意x∈[,]都有f(x)≥0恒成立,
∴k+3≥0,即﹣3≤k<0,
当k=0时,f(x)=3≥0恒成立,
综上所述实数k的取值范围为[﹣3,3],
故答案为:[﹣3,3]
14.【解答】解:===4?==4,
故答案为:4
15.【解答】解:∵已知,x∈(,π),∴2x∈(π,2π),1+2sinxcosx=,
∴sinxcosx=﹣<0,故sinx﹣cosx==(sinx+cosx)2﹣4sinxcosx=,
∴cos2x=(cosx+sinx)(cosx﹣sinx)=?(﹣)=﹣,
故答案为:﹣.
16.【解答】解:设每小时的油耗(所需要的汽油量)为y,
由题意可得y=,
当x=120时,y=11.5,
∴11.5=(120﹣k+),解得k=100,
∴y=(x﹣100+)
∵每小时的油耗不超过9L,
∴(x﹣100+)≤0,
即x2﹣145x+4500≤0,解得45≤x≤100,
又60≤x≤120,可得60≤x≤100,
每小时的油耗不超过9升,x的取值范围为[60,100],
故答案为:[60,100]
三、解答题(本大题共6小题,共计70分.请在答题纸指定区域内作答,解答应写出文字说明,证明过程或演算步骤.)
17.【解答】解:(1)当a=1时,由于lg(x﹣1)>0=lg1,即x﹣1>1,所以A=(2,+∞)
由于x2﹣3x﹣4<0,即(x+1)(x﹣4)<0,所以B=(﹣1,4)
所以A∩B=(2,4);
(2)因为A∪B=A,所以B?A,
由于A=(a+1,+∞),则a+1≤﹣1,
所以a≤﹣2,所以实数a的取值范围为(﹣∞,﹣2].
18.【解答】解:(1)∵A,B均为锐角,sinA=,cos(A+B)=,∴cos2A=1﹣2sin2A=.
(2)由题意cosA==,sin2A=2sinAcosA=,sin(A+B)==,
∴sin(A﹣B)=sin[2A﹣(A+B)]=sin2A?cos(A+B)﹣cos2A?sin(A+B)=?﹣?=.
19.【解答】解:(1)根据用“五点法”画函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的步骤方法,
由所给的表格可得A=2,ω?+φ=,且ω?+φ=2π,
∴ω=2,φ=﹣,∴f(x)=2sin(2x﹣),
可得表格应为:
x
ωx+φ 0 π 2π
Asin(ωx+φ) 0 2 0 ﹣2 0
(2)根据五点法作图,作出函数的一个周期内的图象,
如图:
(3)根据函数的图象以及周期性可得它的减区间为[kπ+,kπ+],k∈Z.
20.【解答】解:(1)y=g(x)=ln2x﹣4lnx+6的定义域是[,e3],
则设t=lnx∈[﹣1,3],
则y=s(t)=t2﹣4t+6=(t﹣2)2+2在[﹣1,2]递减,在[2,3]递增,
故ymin=s(2)=2,
∵s(﹣1)>s(3),则ymax=s(﹣1)=11;
(2)函数h(x)=f(x2)+|x|=2ln|x|+|x|,x∈(﹣∞,0)∪(0,+∞),
∵h(﹣x)=2ln|﹣x|+|﹣x|=2ln|x|+|x|=h(x),故h(x)是偶函数,
当x>0时,h(x)=2lnx+x在(0,+∞)连续不断,且单调递增,
又h(1)=2ln1+1=1>0,h()=﹣2+<0,
则函数h(x)在(0,+∞)上存在唯一的零点,
由于函数h(x)是偶函数,则函数h(x)在(﹣∞,0)上也存在唯一的零点,
综上,函数h(x)在定义域内零点的个数是2个.
21.【解答】解:(1)因为楼D到楼B、C的距离分别为600m和400m,到楼A的距离为1200m,
所以AD=12百米,BD=6百米,CD=4百米,
因为从楼D看楼A、B的视角为90°,则∠ADB=90°,
则tan∠BAD==,tan∠CAD==,
所以tan∠BAC=tan(∠BAD+∠CAD)===1,
又0<∠BAD+∠CAD<π,即∠BAC∈(0,π),
所以∠BAC=,
则从楼A看楼B,C视角的大小为;
(2)在Rt△ABD和Rt△ACD中,AB==6,
AC==4,
则在Rt△ABM中,AM=ABcosθ=6cosθ,
在Rt△ACN中,AN=ACcos(﹣θ)=4cos(﹣θ),
记矩形开发区AMPN的面积为f(θ),
则f(θ)=AM?AN=4cos(﹣θ)×6cosθ=120cosθcos(﹣θ);
又f(θ)=120cosθ(cosθ+sinθ)=60+60(sin2θ+cos2θ)=60+60sin(2θ+);
当2θ+=时,即θ=时,矩形开发区域AMPN的面积最大.
22.【解答】解:(1)∵函数f(x)≤
∴3x+3﹣x≤,
即9?(3x)2﹣82×3x+9≤0,
即(9?3x﹣1)(3x﹣9)≤0
解得≤3x≤9,
解得﹣2≤x≤2,
故不等式的解集为[﹣2,2].
(2)∵函数f(x)的定义域为R,
∴f(﹣x)=3﹣x+3x=f(x),
∴f(x)为偶函数,
(2)函数f(x)在[0,+∞)上单调递增.
证明如下:在[0,+∞)上任取x1,x2,令x1<x2,
f(x1)﹣f(x2)=+﹣﹣=(﹣)?
∵0≤x1<x2,
∴﹣<0,﹣1>0,
∴f(x1)﹣f(x2)<0,
∴函数f(x)在[0,+∞)上单调递增.
(3)对任意x∈[﹣2,1],不等式f(3x)≥mf2(x)恒成立,即33x+3﹣3x≥m(3x+3﹣x)2,
从而有(3x+3﹣x)(32x+3﹣2x+1)≥m(3x+3﹣x)2恒成立,
∵3x+3﹣x>0,
则等价于32x+3﹣2x+1≥m(3x+3﹣x)恒成立,
令t=3x+3﹣x,则32x+3﹣2x=t2﹣2,
由于f(x)为偶函数,由(2)可知f(x)在(0,+∞)上单调递增,
则函数f(x)在(﹣∞,0)上单调递减,
∵{f(x)|x∈[﹣2,1]}={f(x)|x∈[0,2]},
∴f(0)≤f(x)≤f(2),
∴2≤t≤,
则原不等式等价于t2﹣3≥mt,t∈[2,],
即m≤t﹣在t∈[2,]上恒成立,
设g(t)=t﹣,则g(t)在[2,]上为增函数,
∴g(t)≥g(2)=,
∴m≤
同课章节目录
