人教高中数学选修2-1 第二章 2.4.1抛物线及其标准方程(一)(21张)
文档属性
| 名称 | 人教高中数学选修2-1 第二章 2.4.1抛物线及其标准方程(一)(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-25 15:00:08 | ||
图片预览


文档简介
(第一课时)
人教版·选修1-1·第二章《圆锥曲线与方程》
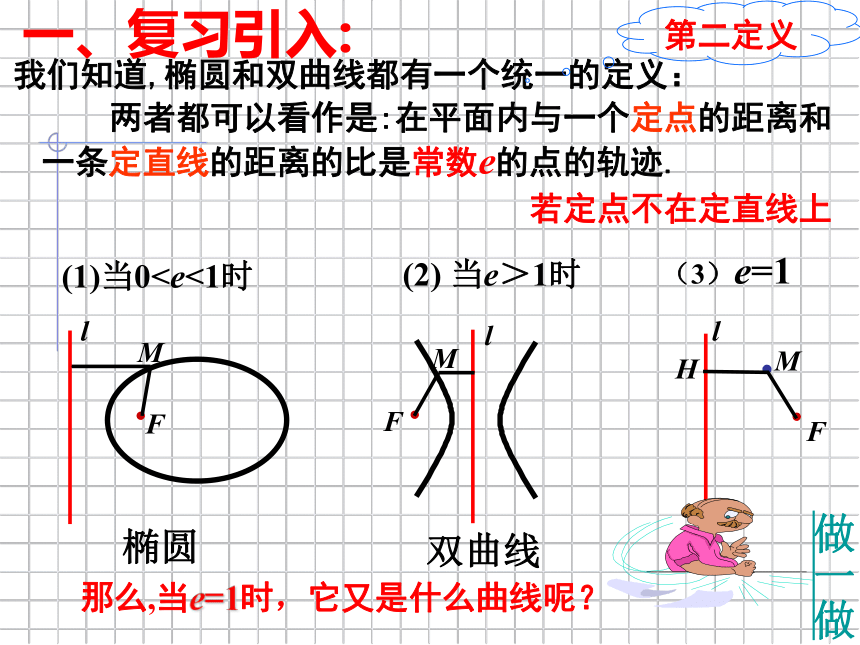
我们知道,椭圆和双曲线都有一个统一的定义:
两者都可以看作是:在平面内与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹.
(2) 当e>1时
(1)当0若定点不在定直线上
那么,当e=1时,它又是什么曲线呢?
一、复习引入:
H
第二定义
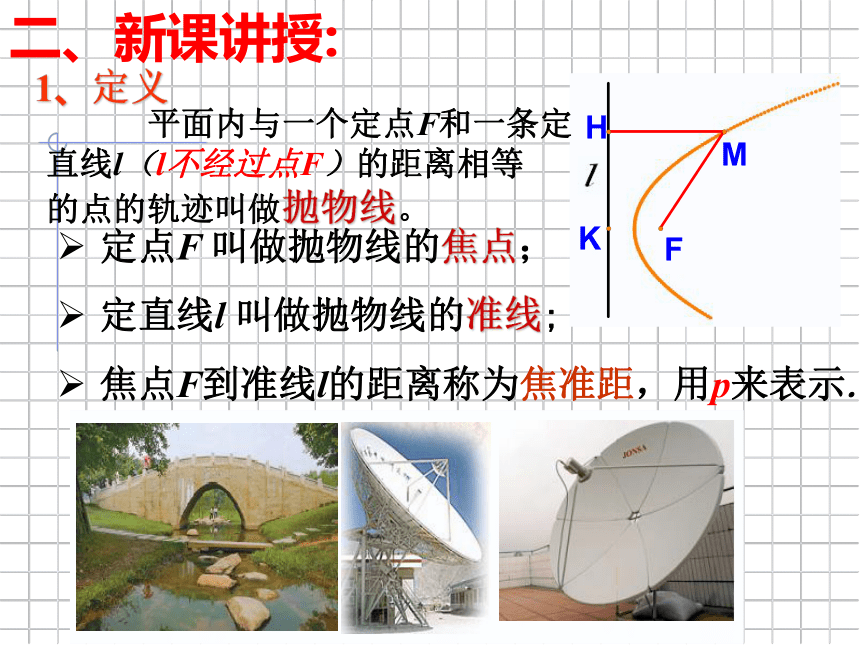
平面内与一个定点F和一条定
直线l(l不经过点F)的距离相等
的点的轨迹叫做抛物线。
1、定义
定点F 叫做抛物线的焦点;
定直线l 叫做抛物线的准线;
焦点F到准线l的距离称为焦准距,用p来表示.
二、新课讲授:
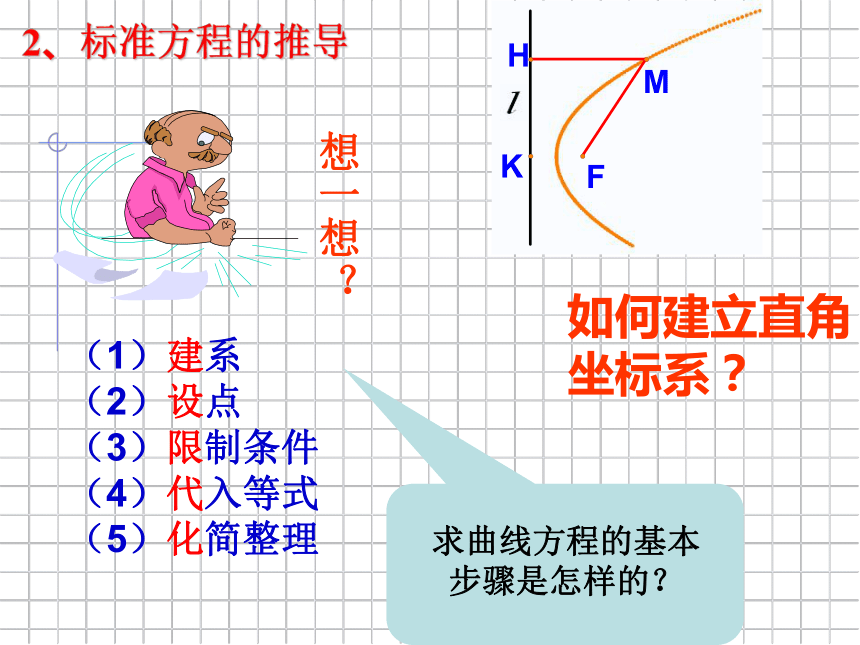
2、标准方程的推导
如何建立直角
坐标系?
(1)建系
(2)设点
(3)限制条件
(4)代入等式
(5)化简整理
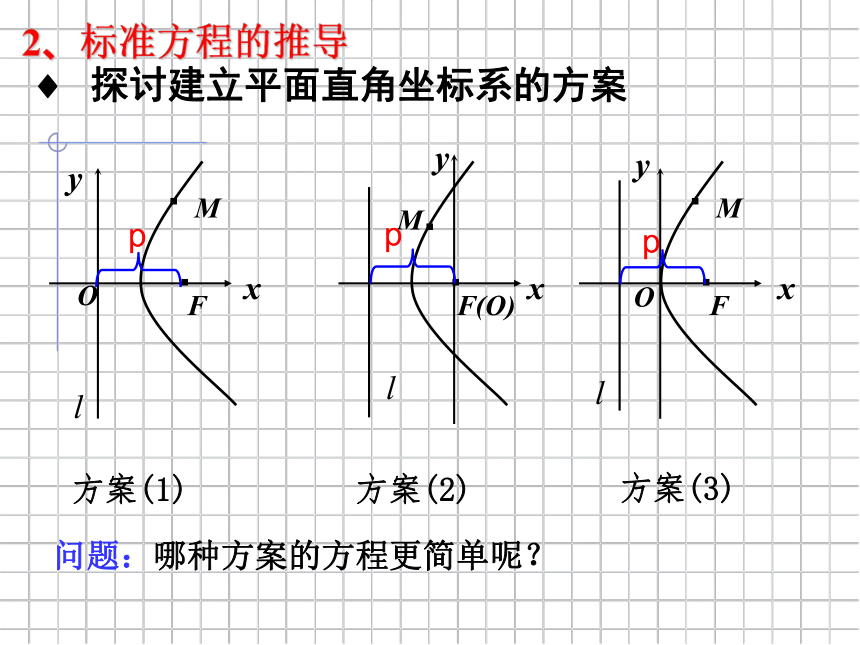
? 探讨建立平面直角坐标系的方案
方案(1)
方案(2)
方案(3)
问题:哪种方案的方程更简单呢?
2、标准方程的推导
p
p
p
H
M(x,y)
F
l
p
2、标准方程的推导
M(x,y)
H
F
l
p
2、标准方程的推导
l
方案三:以过F且垂直于l 的直线为x轴,垂足为K.以F、K的中点O为坐标原点,建立直角坐标系xOy.
化简得:
M(x,y)
F
H
p
2、标准方程的推导
比较三种方案推导出的方程,哪种更简单?
方案(1)
方案(2)
方案(3)
2、标准方程的推导
O
x
再次提醒:
p的几何意义是:焦点到准线的距离,
故称焦准距。
y
3、抛物线的标准方程
平面内与一个定点F 和一条定
直线l(l不经过点F)的距离相等
的点的轨迹是抛物线.
一般情况
平面内与一个定点F 和一条定
直线l(l经过点F)的距离相等
的点的轨迹是什么?
特殊情况
答:一条直线
你能否写出开口向左,顶点在原点,焦点在坐标轴上的抛物线的标准方程?
思考一:
y2=-2px
你能否分别写出开口向上、向下,顶点在原点,焦点在坐标轴上的抛物线的标准方程?
思考二:
(3)
(4)
x2=2py
(p>0)
x2=-2py
(p>0)
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
焦点坐标
准线方程
标准方程
p:
焦点到准线的距离
抛物线标准方程的特征:
等号左边是系数为1的二次项,右边是一次项.
小结:
(1)一次项定轴,系数正负定方向;
(2)焦点与方程同号,准线与方程异号.
4、四种形式抛物线的对比
图 形
三、例题讲解
解:
例2 根据已知条件,求抛物线的标准方程.
(1)经过点(2 , 2);
(2)焦点在直线x+y+1=0上.
(2)焦点是直线x+y+1=0与坐标轴的交点, 故
或 ,所以 ,故方程为 或
(1)标准方程为 或 ,将点(2 , 2)
例3.一种卫星接收天线的轴截面如下图所示.卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处.
已知接收天线的径口(直径)为4.8m,深度为0.5m. 建立适当的坐标系,求抛物线的标准方程和焦点坐标。
0.5m
4.8m
解:如上图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合.
设抛物线的标准方程是 y2=2px (p>0) ,由已知条件可得,点A的坐标是(0.5,2.4) ,代入方程,得2.42=2p×0.5, ∴p=5.76
∴所求抛物线的标准方程是 y2=11.56x,
焦点的坐标是F(2.88,0)
4.8m
(0.5,2.4)
0.5m
x的范围是[0,0.5]
四、反馈练习
1、求下列抛物线的焦点坐标和准线方程
2、根据下列条件写出抛物线的标准方程
1、掌握抛物线的定义。
平面内与一个定点F和一条定直线l(l不经过点F)
的距离相等的点的轨迹叫做抛物线。
2、深化曲线方程的求解方法:
(1)建系;(2)设点;(3)限制条件;
(4)代入等式 ;(5)化简整理
3、掌握并理解抛物线的四种形式的标准方程.
注:①p的几何意义是:焦点到准线的距离(焦准距);
②对称轴看一次项系数,符号确定开口方向.
五、课堂小结
六、作业布置
教材p64 练习A组2.3的1、2、3、4、5、6;
灰皮p30 §2.4.1“抛物线标准方程(一)”
课外练习
1、求抛物线 的焦点和准线方程;
2、求过点A(-3,2)的抛物线的标准方程.
人教版·选修1-1·第二章《圆锥曲线与方程》
我们知道,椭圆和双曲线都有一个统一的定义:
两者都可以看作是:在平面内与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹.
(2) 当e>1时
(1)当0
那么,当e=1时,它又是什么曲线呢?
一、复习引入:
H
第二定义
平面内与一个定点F和一条定
直线l(l不经过点F)的距离相等
的点的轨迹叫做抛物线。
1、定义
定点F 叫做抛物线的焦点;
定直线l 叫做抛物线的准线;
焦点F到准线l的距离称为焦准距,用p来表示.
二、新课讲授:
2、标准方程的推导
如何建立直角
坐标系?
(1)建系
(2)设点
(3)限制条件
(4)代入等式
(5)化简整理
? 探讨建立平面直角坐标系的方案
方案(1)
方案(2)
方案(3)
问题:哪种方案的方程更简单呢?
2、标准方程的推导
p
p
p
H
M(x,y)
F
l
p
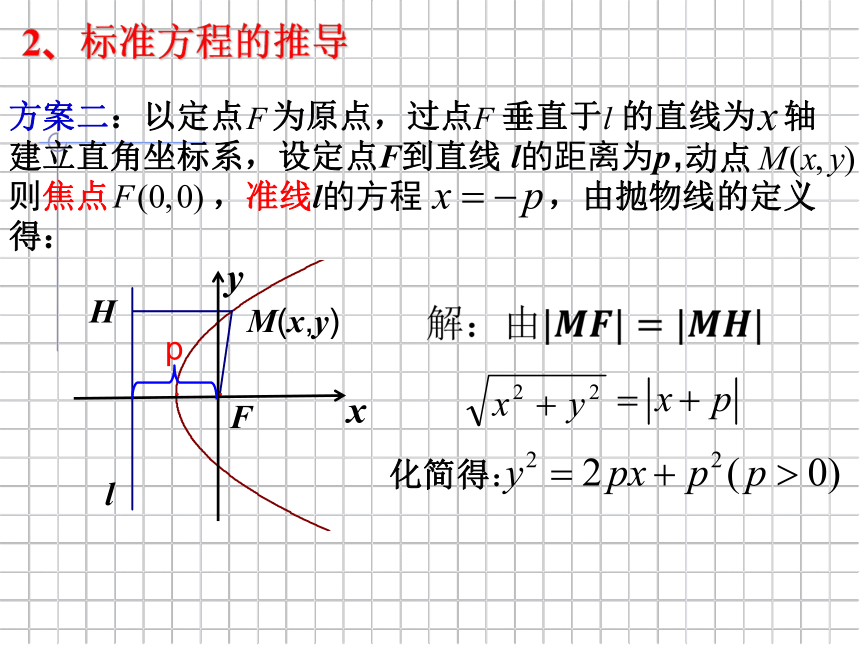
2、标准方程的推导
M(x,y)
H
F
l
p
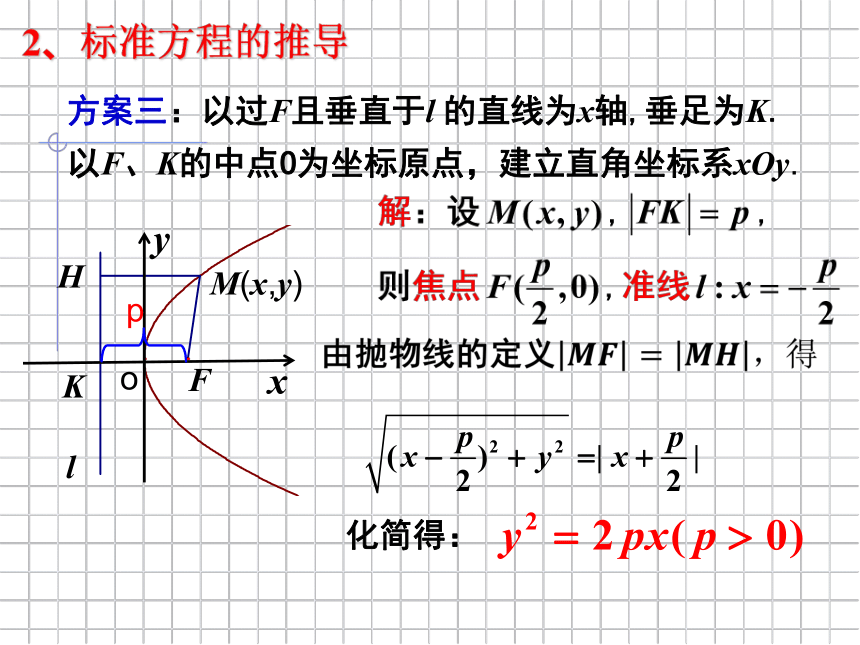
2、标准方程的推导
l
方案三:以过F且垂直于l 的直线为x轴,垂足为K.以F、K的中点O为坐标原点,建立直角坐标系xOy.
化简得:
M(x,y)
F
H
p
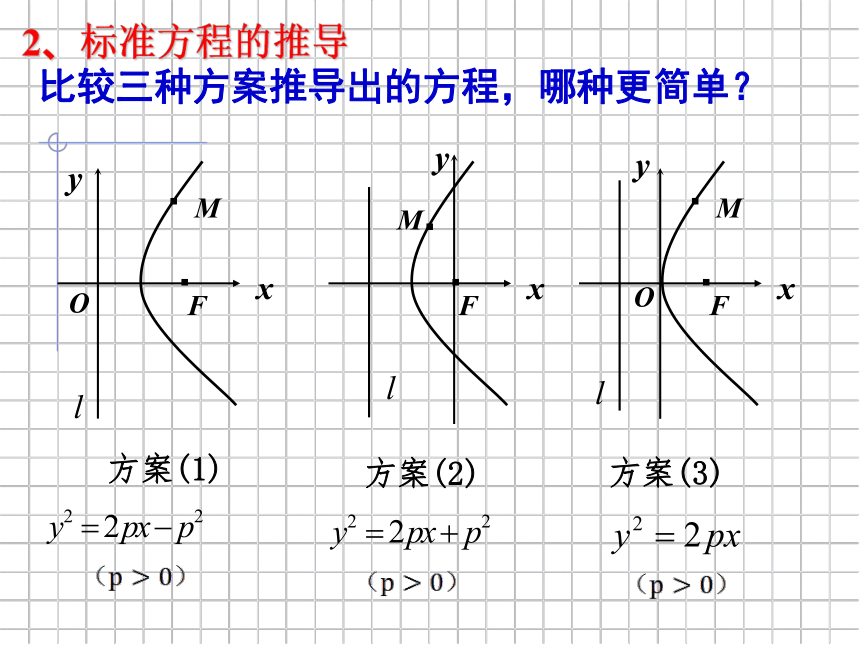
2、标准方程的推导
比较三种方案推导出的方程,哪种更简单?
方案(1)
方案(2)
方案(3)
2、标准方程的推导
O
x
再次提醒:
p的几何意义是:焦点到准线的距离,
故称焦准距。
y
3、抛物线的标准方程
平面内与一个定点F 和一条定
直线l(l不经过点F)的距离相等
的点的轨迹是抛物线.
一般情况
平面内与一个定点F 和一条定
直线l(l经过点F)的距离相等
的点的轨迹是什么?
特殊情况
答:一条直线
你能否写出开口向左,顶点在原点,焦点在坐标轴上的抛物线的标准方程?
思考一:
y2=-2px
你能否分别写出开口向上、向下,顶点在原点,焦点在坐标轴上的抛物线的标准方程?
思考二:
(3)
(4)
x2=2py
(p>0)
x2=-2py
(p>0)
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
焦点坐标
准线方程
标准方程
p:
焦点到准线的距离
抛物线标准方程的特征:
等号左边是系数为1的二次项,右边是一次项.
小结:
(1)一次项定轴,系数正负定方向;
(2)焦点与方程同号,准线与方程异号.
4、四种形式抛物线的对比
图 形
三、例题讲解
解:
例2 根据已知条件,求抛物线的标准方程.
(1)经过点(2 , 2);
(2)焦点在直线x+y+1=0上.
(2)焦点是直线x+y+1=0与坐标轴的交点, 故
或 ,所以 ,故方程为 或
(1)标准方程为 或 ,将点(2 , 2)
例3.一种卫星接收天线的轴截面如下图所示.卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处.
已知接收天线的径口(直径)为4.8m,深度为0.5m. 建立适当的坐标系,求抛物线的标准方程和焦点坐标。
0.5m
4.8m
解:如上图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合.
设抛物线的标准方程是 y2=2px (p>0) ,由已知条件可得,点A的坐标是(0.5,2.4) ,代入方程,得2.42=2p×0.5, ∴p=5.76
∴所求抛物线的标准方程是 y2=11.56x,
焦点的坐标是F(2.88,0)
4.8m
(0.5,2.4)
0.5m
x的范围是[0,0.5]
四、反馈练习
1、求下列抛物线的焦点坐标和准线方程
2、根据下列条件写出抛物线的标准方程
1、掌握抛物线的定义。
平面内与一个定点F和一条定直线l(l不经过点F)
的距离相等的点的轨迹叫做抛物线。
2、深化曲线方程的求解方法:
(1)建系;(2)设点;(3)限制条件;
(4)代入等式 ;(5)化简整理
3、掌握并理解抛物线的四种形式的标准方程.
注:①p的几何意义是:焦点到准线的距离(焦准距);
②对称轴看一次项系数,符号确定开口方向.
五、课堂小结
六、作业布置
教材p64 练习A组2.3的1、2、3、4、5、6;
灰皮p30 §2.4.1“抛物线标准方程(一)”
课外练习
1、求抛物线 的焦点和准线方程;
2、求过点A(-3,2)的抛物线的标准方程.
