北师大版八年级数学下册:1.3 线段的垂直平分线课件 (共33张PPT)
文档属性
| 名称 | 北师大版八年级数学下册:1.3 线段的垂直平分线课件 (共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 454.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-24 22:53:01 | ||
图片预览









文档简介
1.3 线段的垂直平分线
线段垂直平分线的性质
拿出准备好的纸,按照下图的样子进行对折,并比较对折之后的折痕EB和EB′ , FB和FB′的关系.
B
B′
E
F
E
F
B
(B′)
折痕EB=EB′ , FB=FB′
上面的结论是比较直观和明显的,我们可以说出两组边分别是相等的,但是,我们可以用观察的方法说服别人吗?
在数学中,光靠观察是不够的,还需要理性的证明.
线段垂直平分线的性质
如何证明这个结论呢?
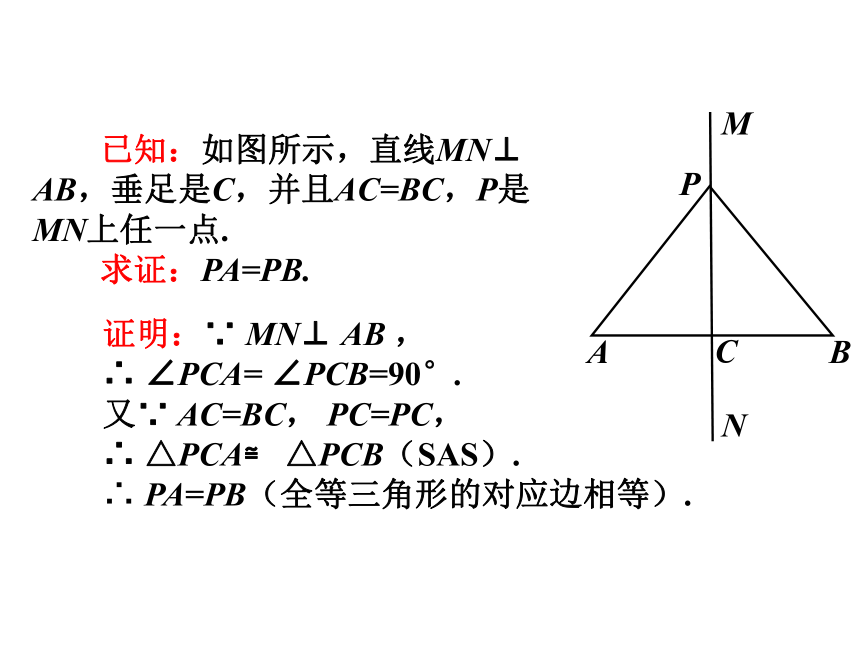
已知:如图所示,直线MN⊥ AB,垂足是C,并且AC=BC,P是MN上任一点.
求证:PA=PB.
A
B
C
N
P
M
证明:∵ MN⊥ AB ,
∴ ∠PCA= ∠PCB=90°.
又∵ AC=BC, PC=PC,
∴ △PCA≌ △PCB(SAS).
∴ PA=PB(全等三角形的对应边相等).
线段垂直平分线的性质
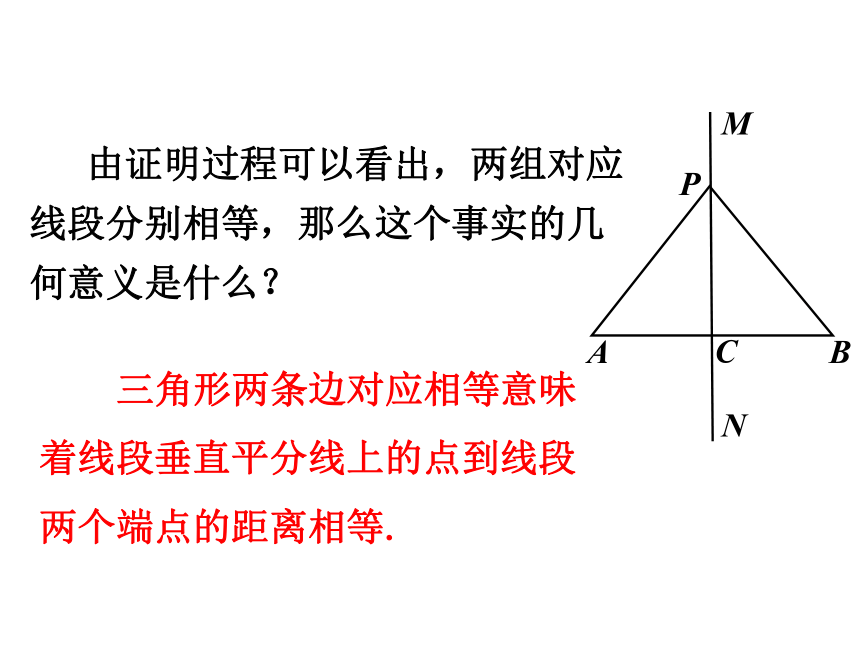
由证明过程可以看出,两组对应线段分别相等,那么这个事实的几何意义是什么?
三角形两条边对应相等意味着线段垂直平分线上的点到线段两个端点的距离相等.
线段垂直平分线的性质
A
B
C
N
P
M
线段垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
线段垂直平分线的性质
定理中说线段垂直平分线上的任一点到线段两个端点的距离相等,但是在证明过程中,只是随机选了一种情况来证明,这并不影响定理的正确性,因为所选的点是任意的.
你还记得上节课学过的关于互逆命题和互逆定理的知识吗?
线段垂直平分线的判定
逆命题定义:在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
逆定理定义:一个命题是真命题,它的逆命题不一定是真命题.如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理.
线段垂直平分线的判定
你能说说自己收集到的数学上的互逆命题和互逆定理吗?
线段垂直平分线的判定
如果命题不是“如果……那么……”的形式,怎么找出它的逆命题呢?
运用转化的思想,先找到原命题的条件和结论,把命题写成“如果……那么……”的形式,然后再写出它的逆命题,最后再对命题的形式进行整理.
线段垂直平分线的判定
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
逆命题:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
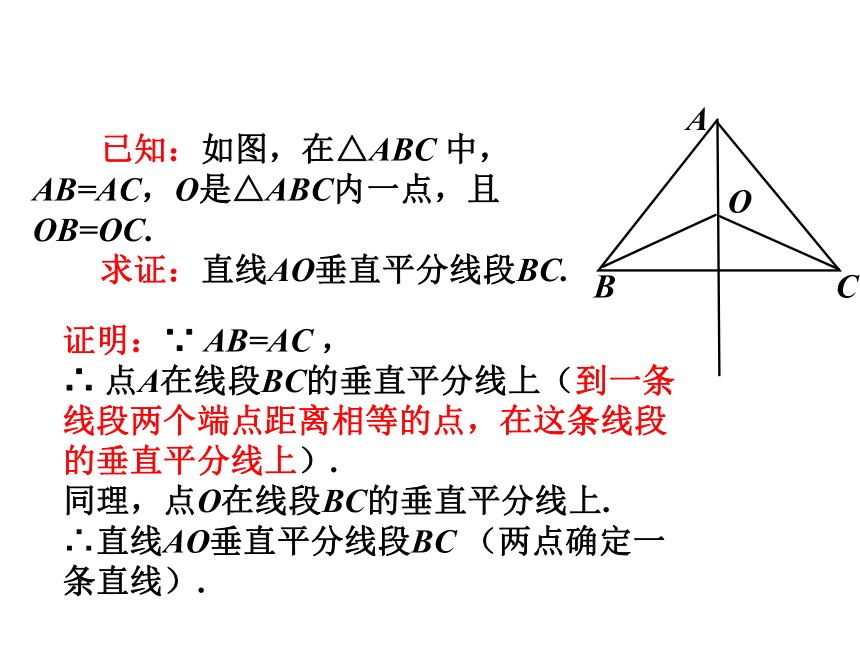
已知:如图,在△ABC 中,AB=AC,O是△ABC内一点,且OB=OC.
求证:直线AO垂直平分线段BC.
B
C
O
A
证明:∵ AB=AC ,
∴ 点A在线段BC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
同理,点O在线段BC的垂直平分线上.
∴直线AO垂直平分线段BC (两点确定一条直线).
线段垂直平分线的判定
线段垂直平分线的判定
课下作业:
收集生活中应用线段的垂直平分线的例子,体会线段垂直平分线的判定定理的应用.
用尺规作线段的垂直平分线
欣赏
用尺规作线段的垂直平分线
中国篇
俗话说:“不以规矩,不成方圆”,究竟什么是“规”,什么是“矩”?????
“规”就是圆规,是用来画圆的工具,在我国古代甲骨文中就有“规”这个字.“矩”就像现在木工使用的角尺,由长短两尺相交成直角而成,两者间用木杠连接以使其牢固,其中短尺叫勾,长尺叫股.???
矩的使用是我国古代的一个发明,山东历城武梁祠石室造像中就有“伏羲氏手执矩,女娲氏手执规”之图形.矩不仅可以画直线、直角,加上刻度可以测量,还可以代替圆规.甲骨文中也有矩字,这可追溯到大禹治水(公元前2000年)前.???
用尺规作线段的垂直平分线
国际篇
古代希腊人较重视规、矩在数学中训练思维和智力的作用,而忽视规、矩的实用价值.因此,在作图中对规、矩的使用方法加以很多限制,提出了尺规作图问题.所谓尺规作图,就是只有限次地使用没有刻度的直尺和圆规进行作图.???
古希腊的安那萨哥拉斯首先提出作图要有尺寸限制.他因政治上的纠葛,被关进监狱,并被处以死刑.在监狱里,他思考改圆成方以及其他有关问题,用来打发令人苦恼的无所事事的生活.他不可能有规范的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度.另外,对他来说,时间是不多了,因此他很自然地想到要有限次地使用尺规解决问题.后来以理论形式具体明确这个规定的是欧几里德的《几何原本》.由于《几何原本》的巨大影响,希腊人所崇尚的尺规作图也一直被遵守并流传下来.
用尺规作线段的垂直平分线
几何三大难题:
(1)三等分角问题:将任一个给定的角三等分;?
(2)立方倍积问题:求作一个正方体的棱长,使这个正方体的体积是已知正方体体积的二倍;???
(3)化圆为方问题:求作一个正方形,使它的面积和已知圆的面积相等.
用尺规作线段的垂直平分线
基本作图:作线段的垂直平分线.
已知:线段AB.
求作:线段AB的垂直平分线.
作法:(1)分别以A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD,CD即为所求.
A
B
C
D
线段垂直平分线的性质定理
拿出准备好的三角形纸片,按照下图的样子进行折叠,找出每条边的垂直平分线.
观察:折出来的三条垂直平分线有什么关系?
线段垂直平分线的性质定理
三条垂直平分线交于一点
利用圆规和直尺,画一个任意的三角形,并利用所学知识作出三角形三条边的垂直平分线.
已知:△ABC.
求作: △ABC三边的垂直平分线.
线段垂直平分线的性质定理
A
B
C
作法:(1)分别以B,C为圆心,以大于 BC的长为半径作弧,两弧交于E,F两点.(2)作直线EF, EF即为BC边上的垂直平分线.
同理作出AB,AC边上的垂直平分线.
E
F
不管是什么样的三角形,它们的垂直平分线有没有什么共性?有的话,这个共性是什么?试着猜想一下!
线段垂直平分线的性质定理
A
B
C
猜想:
三条垂直平分线交于一点
你是怎么得到这个猜想的?
线段垂直平分线的性质定理
A
B
C
准确的图形可以直观地揭示数学对象的性质,因此有利于发现数学结论,因此我们要养成认真画图的好习惯.
猜想:
三条垂直平分线交于一点
思考:我们知道两条直线交于一点,要证明三条直线相交于一点,是不是只要证明第三条直线也通过这两条直线的交点就可以呢?
线段垂直平分线的性质定理
只要能证明其中两条直线的交点在第三条直线上就可以了.
三条垂直平分线除了交于一点外,还有什么性质?
线段垂直平分线的性质定理
观察,用直尺测量,发现公共点到三个顶点的距离相等.
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
线段垂直平分线的性质定理
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC的垂直平分线经过点P ,且PA=PB=PC.
A
B
C
P
线段垂直平分线的性质定理
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC的垂直平分线经过点P ,且PA=PB=PC.
A
B
C
P
证明:∵点P 在线段AB的垂直平分线上,
∴ PA=PB(线段垂直平分线上的点到这条线段两个端点的距离相等).
同理,PB=PC.
∴ PA=PB=PC.
∴点P 在线段AC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
即边AC的垂直平分线经过点P.
分组讨论:已知三角形的一条边及这条边上的高, 你能作出三角形吗?如果能,能作几个?所作出的三角形都全等吗?
作图的问题
能作出无数个
所作出的三角形不全等
你能试着画出符合要求的三角形吗?试试吧!
作图的问题
已知:线段a,h.
求作: △ABC,使BC=a,BC上的高AD= h.
已知三角形的一条边及这条边上的高, 求作三角形.
a
h
A
B
C
D
l
作法:(1)作线段BC=a.
(2)在线段BC上任取一点D ,过点D作线段BC的垂线l.
(3)在l上作线段DA,使DA= h.
(4)连接AB,AC.
△ABC为所求作的三角形.
已知底边及底边上的高,求作等腰三角形
已知一个等腰三角形的底边及底边上的高, 求作这个等腰三角形.
已知:如图,线段a,h.
求作: △ABC,使AB=AC,且BC=a,高AD= h.
a
h
A
B
C
D
l
作法:(1)作线段BC=a.
(2)作线段BC的垂直平分线l,交BC于点D.
(3)在l上作线段DA,使DA= h.
(4)连接AB,AC.
△ABC为所求作的等腰三角形.
教材“做一做”
已知直线l和l上一点P,用尺规作l的垂线,使它经过点P.
小明的作法如图.
你能明白小明的作法吗?
你是怎样作的?
小明是在l上任取线段AB,然后作线段AB的垂直平分线,即直线l的垂线.
教材“做一做”
议一议:如果点P是直线l外一点,那么怎样用尺规作l的垂线,使它经过点P呢?说说你的作法,并与同伴交流.
作法:如图.(1)任取一点K,使K和P在l的两旁.
(2)以P为圆心,PK的长为半径作弧,交l于点D和E.
(3)分别以D和E为圆心,大于 DE的长为半径作弧,两弧交于点F.
(4)作直线PF.
直线PF就是所求的垂线.
通过这节课的学习,你学到了什么知识?
课堂小结
谢谢大家!
再见!
线段垂直平分线的性质
拿出准备好的纸,按照下图的样子进行对折,并比较对折之后的折痕EB和EB′ , FB和FB′的关系.
B
B′
E
F
E
F
B
(B′)
折痕EB=EB′ , FB=FB′
上面的结论是比较直观和明显的,我们可以说出两组边分别是相等的,但是,我们可以用观察的方法说服别人吗?
在数学中,光靠观察是不够的,还需要理性的证明.
线段垂直平分线的性质
如何证明这个结论呢?
已知:如图所示,直线MN⊥ AB,垂足是C,并且AC=BC,P是MN上任一点.
求证:PA=PB.
A
B
C
N
P
M
证明:∵ MN⊥ AB ,
∴ ∠PCA= ∠PCB=90°.
又∵ AC=BC, PC=PC,
∴ △PCA≌ △PCB(SAS).
∴ PA=PB(全等三角形的对应边相等).
线段垂直平分线的性质
由证明过程可以看出,两组对应线段分别相等,那么这个事实的几何意义是什么?
三角形两条边对应相等意味着线段垂直平分线上的点到线段两个端点的距离相等.
线段垂直平分线的性质
A
B
C
N
P
M
线段垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
线段垂直平分线的性质
定理中说线段垂直平分线上的任一点到线段两个端点的距离相等,但是在证明过程中,只是随机选了一种情况来证明,这并不影响定理的正确性,因为所选的点是任意的.
你还记得上节课学过的关于互逆命题和互逆定理的知识吗?
线段垂直平分线的判定
逆命题定义:在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
逆定理定义:一个命题是真命题,它的逆命题不一定是真命题.如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理.
线段垂直平分线的判定
你能说说自己收集到的数学上的互逆命题和互逆定理吗?
线段垂直平分线的判定
如果命题不是“如果……那么……”的形式,怎么找出它的逆命题呢?
运用转化的思想,先找到原命题的条件和结论,把命题写成“如果……那么……”的形式,然后再写出它的逆命题,最后再对命题的形式进行整理.
线段垂直平分线的判定
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
逆命题:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
已知:如图,在△ABC 中,AB=AC,O是△ABC内一点,且OB=OC.
求证:直线AO垂直平分线段BC.
B
C
O
A
证明:∵ AB=AC ,
∴ 点A在线段BC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
同理,点O在线段BC的垂直平分线上.
∴直线AO垂直平分线段BC (两点确定一条直线).
线段垂直平分线的判定
线段垂直平分线的判定
课下作业:
收集生活中应用线段的垂直平分线的例子,体会线段垂直平分线的判定定理的应用.
用尺规作线段的垂直平分线
欣赏
用尺规作线段的垂直平分线
中国篇
俗话说:“不以规矩,不成方圆”,究竟什么是“规”,什么是“矩”?????
“规”就是圆规,是用来画圆的工具,在我国古代甲骨文中就有“规”这个字.“矩”就像现在木工使用的角尺,由长短两尺相交成直角而成,两者间用木杠连接以使其牢固,其中短尺叫勾,长尺叫股.???
矩的使用是我国古代的一个发明,山东历城武梁祠石室造像中就有“伏羲氏手执矩,女娲氏手执规”之图形.矩不仅可以画直线、直角,加上刻度可以测量,还可以代替圆规.甲骨文中也有矩字,这可追溯到大禹治水(公元前2000年)前.???
用尺规作线段的垂直平分线
国际篇
古代希腊人较重视规、矩在数学中训练思维和智力的作用,而忽视规、矩的实用价值.因此,在作图中对规、矩的使用方法加以很多限制,提出了尺规作图问题.所谓尺规作图,就是只有限次地使用没有刻度的直尺和圆规进行作图.???
古希腊的安那萨哥拉斯首先提出作图要有尺寸限制.他因政治上的纠葛,被关进监狱,并被处以死刑.在监狱里,他思考改圆成方以及其他有关问题,用来打发令人苦恼的无所事事的生活.他不可能有规范的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度.另外,对他来说,时间是不多了,因此他很自然地想到要有限次地使用尺规解决问题.后来以理论形式具体明确这个规定的是欧几里德的《几何原本》.由于《几何原本》的巨大影响,希腊人所崇尚的尺规作图也一直被遵守并流传下来.
用尺规作线段的垂直平分线
几何三大难题:
(1)三等分角问题:将任一个给定的角三等分;?
(2)立方倍积问题:求作一个正方体的棱长,使这个正方体的体积是已知正方体体积的二倍;???
(3)化圆为方问题:求作一个正方形,使它的面积和已知圆的面积相等.
用尺规作线段的垂直平分线
基本作图:作线段的垂直平分线.
已知:线段AB.
求作:线段AB的垂直平分线.
作法:(1)分别以A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD,CD即为所求.
A
B
C
D
线段垂直平分线的性质定理
拿出准备好的三角形纸片,按照下图的样子进行折叠,找出每条边的垂直平分线.
观察:折出来的三条垂直平分线有什么关系?
线段垂直平分线的性质定理
三条垂直平分线交于一点
利用圆规和直尺,画一个任意的三角形,并利用所学知识作出三角形三条边的垂直平分线.
已知:△ABC.
求作: △ABC三边的垂直平分线.
线段垂直平分线的性质定理
A
B
C
作法:(1)分别以B,C为圆心,以大于 BC的长为半径作弧,两弧交于E,F两点.(2)作直线EF, EF即为BC边上的垂直平分线.
同理作出AB,AC边上的垂直平分线.
E
F
不管是什么样的三角形,它们的垂直平分线有没有什么共性?有的话,这个共性是什么?试着猜想一下!
线段垂直平分线的性质定理
A
B
C
猜想:
三条垂直平分线交于一点
你是怎么得到这个猜想的?
线段垂直平分线的性质定理
A
B
C
准确的图形可以直观地揭示数学对象的性质,因此有利于发现数学结论,因此我们要养成认真画图的好习惯.
猜想:
三条垂直平分线交于一点
思考:我们知道两条直线交于一点,要证明三条直线相交于一点,是不是只要证明第三条直线也通过这两条直线的交点就可以呢?
线段垂直平分线的性质定理
只要能证明其中两条直线的交点在第三条直线上就可以了.
三条垂直平分线除了交于一点外,还有什么性质?
线段垂直平分线的性质定理
观察,用直尺测量,发现公共点到三个顶点的距离相等.
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
线段垂直平分线的性质定理
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC的垂直平分线经过点P ,且PA=PB=PC.
A
B
C
P
线段垂直平分线的性质定理
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC的垂直平分线经过点P ,且PA=PB=PC.
A
B
C
P
证明:∵点P 在线段AB的垂直平分线上,
∴ PA=PB(线段垂直平分线上的点到这条线段两个端点的距离相等).
同理,PB=PC.
∴ PA=PB=PC.
∴点P 在线段AC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
即边AC的垂直平分线经过点P.
分组讨论:已知三角形的一条边及这条边上的高, 你能作出三角形吗?如果能,能作几个?所作出的三角形都全等吗?
作图的问题
能作出无数个
所作出的三角形不全等
你能试着画出符合要求的三角形吗?试试吧!
作图的问题
已知:线段a,h.
求作: △ABC,使BC=a,BC上的高AD= h.
已知三角形的一条边及这条边上的高, 求作三角形.
a
h
A
B
C
D
l
作法:(1)作线段BC=a.
(2)在线段BC上任取一点D ,过点D作线段BC的垂线l.
(3)在l上作线段DA,使DA= h.
(4)连接AB,AC.
△ABC为所求作的三角形.
已知底边及底边上的高,求作等腰三角形
已知一个等腰三角形的底边及底边上的高, 求作这个等腰三角形.
已知:如图,线段a,h.
求作: △ABC,使AB=AC,且BC=a,高AD= h.
a
h
A
B
C
D
l
作法:(1)作线段BC=a.
(2)作线段BC的垂直平分线l,交BC于点D.
(3)在l上作线段DA,使DA= h.
(4)连接AB,AC.
△ABC为所求作的等腰三角形.
教材“做一做”
已知直线l和l上一点P,用尺规作l的垂线,使它经过点P.
小明的作法如图.
你能明白小明的作法吗?
你是怎样作的?
小明是在l上任取线段AB,然后作线段AB的垂直平分线,即直线l的垂线.
教材“做一做”
议一议:如果点P是直线l外一点,那么怎样用尺规作l的垂线,使它经过点P呢?说说你的作法,并与同伴交流.
作法:如图.(1)任取一点K,使K和P在l的两旁.
(2)以P为圆心,PK的长为半径作弧,交l于点D和E.
(3)分别以D和E为圆心,大于 DE的长为半径作弧,两弧交于点F.
(4)作直线PF.
直线PF就是所求的垂线.
通过这节课的学习,你学到了什么知识?
课堂小结
谢谢大家!
再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
