安徽省赛口中学2018-2019学年高二下学期开学考试数学试卷 Word版含答案
文档属性
| 名称 | 安徽省赛口中学2018-2019学年高二下学期开学考试数学试卷 Word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 283.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-25 00:00:00 | ||
图片预览



文档简介
安徽省赛口中学2018-2019学年高二下学期开学考试
数学试卷
一、单选题(本大题共12小题,每小题5分,共60分)
1.下列判断中正确的是( )
A. “若,则有实数根”的逆命题是真命题
B. “”是“直线与直线平行”的充要条件
C. 命题“”是真命题
D. 命题“”在时是假命题
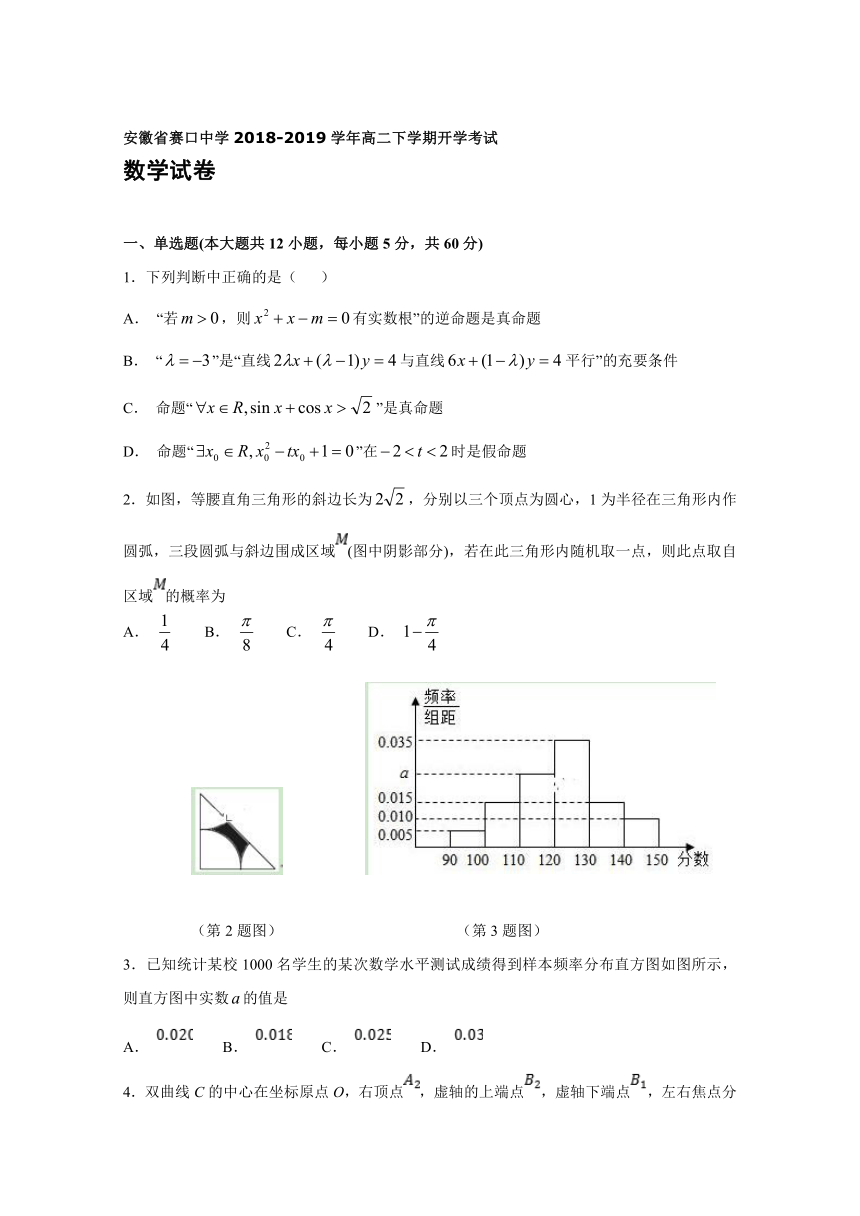
2.如图,等腰直角三角形的斜边长为,分别以三个顶点为圆心,1为半径在三角形内作圆弧,三段圆弧与斜边围成区域(图中阴影部分),若在此三角形内随机取一点,则此点取自区域的概率为
A. B. C. D.
(第2题图) (第3题图)
3.已知统计某校1000名学生的某次数学水平测试成绩得到样本频率分布直方图如图所示,则直方图中实数的值是
A. B. C. D.
4.双曲线C的中心在坐标原点O,右顶点,虚轴的上端点,虚轴下端点,左右焦点分别为、,直线与直线交于P点,若为锐角,则双曲线C的离心率的取值范围为
A. B. C. D.
5.若命题“”为假命题,则的取值范围是( )
A. B. C. D.
6. P是双曲线左支上的一点,F1、F2分别是左、右焦点,且焦距为2c,则的内切圆的圆心的横坐标为( )
(A) (B) (C) (D)
7.已知分别为椭圆的左右焦点,点在椭圆上,当时,则点横坐标的取值范围是( )
A. B. C. D.
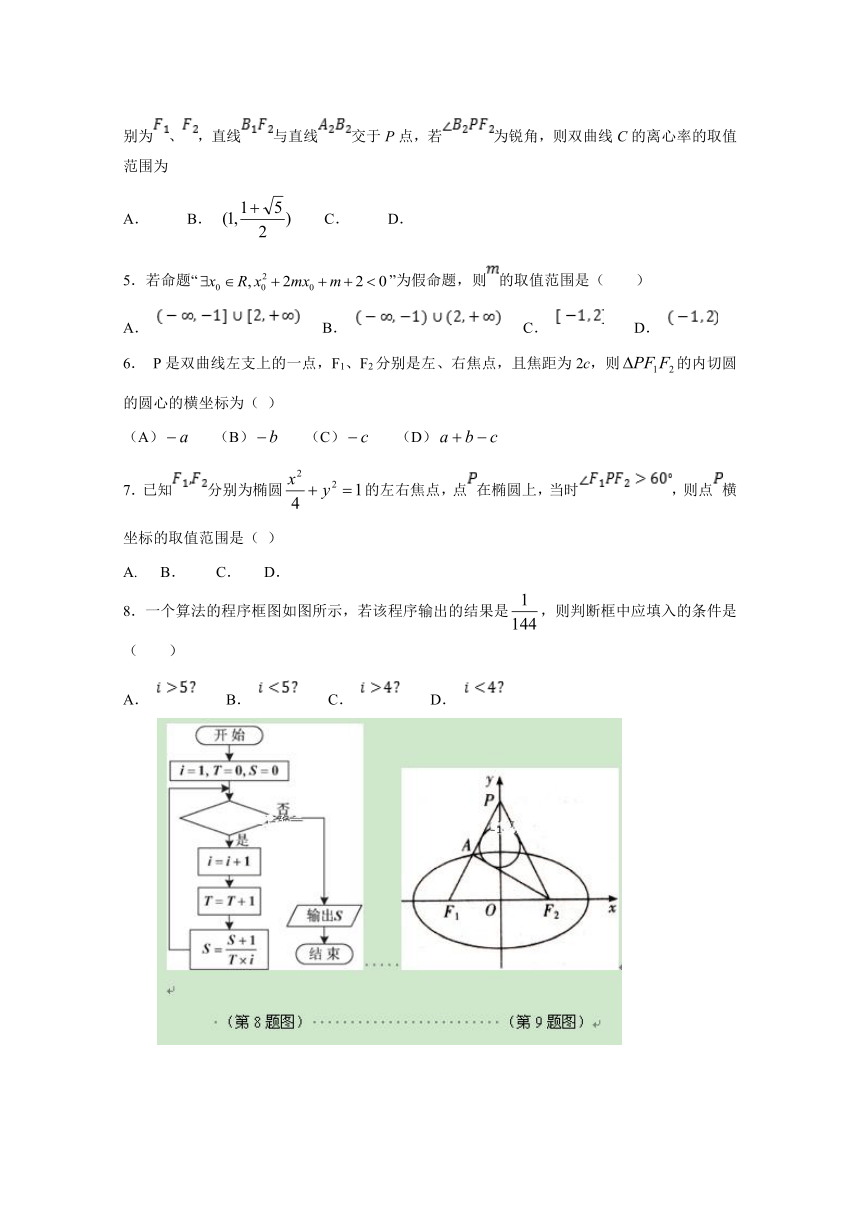
8.一个算法的程序框图如图所示,若该程序输出的结果是,则判断框中应填入的条件是( )
A. B. C. D.
9.如图,已知椭圆的左,右焦点分别为,,是轴正半轴上一点,交椭圆于A,若,且的内切圆半径为,则椭圆的离心率为( )
A. B. C. D.
10.过双曲线的右焦点作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B,若,则双曲线的渐近线方程为( )
A. B. C. D.
11.采用系统抽样方法从人中抽取人做问卷调查,为此将他们随机编号为,,,,分组后某组抽到的号码为41.抽到的人中,编号落入区间 的人数为( )
A. 10 B. 1 C.12 D. 13
12.若点A,F分别是椭圆的左顶点和左焦点,过点F的直线交椭圆于M,N两点,记直线的斜率为,其满足,则直线的斜率为
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.某同学同时掷两颗均匀正方形骰子,得到的点数分别为,则椭圆的离心率的概率是__________.
14.椭圆的左、右焦点分别为,顶点到的距离为4,直线上存在点,使得为底角是的等腰三角形,则此椭圆方程为__________.
15.某校高中年级开设了丰富多彩的校本课程,甲、乙两班各随机抽取了5名学生的学分,用茎叶图表示(如右图).,分别表示甲、乙两班各自5名学生学分的标准差,则 .(填“”、“”或“=”)
16.已知是椭圆与双曲线的公共焦点,是它们的一个公共点,且,线段的垂直平分线过,若椭圆的离心率为,双曲线的离心率为,则的最小值为____________.
三、解答题(本大题共6小题,共70分,其中17题10分,其它题目每题12分)
17.已知命题,;命题:关于的方程有两个不同的实数根.
(1)若为真命题,求实数的取值范围;
(2)若为真命题,为假命题,求实数的取值范围.
已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为,右顶点为,
(1)求该椭圆的标准方程;
(2)(文)若是椭圆上的动点,过P作垂直于x轴的垂线,垂足为M,延长MP至N,使得P恰好为MN中点,求点N的轨迹方程;
(理)若已知点,是椭圆上的动点,求线段中点的轨迹方程;
19.某位同学进行社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了12月11日至12月15日的白天平均气温 (℃)与该小卖部的这种饮料销量(杯),得到如下数据:
日期
12月11日
12月12日
12月13日
12月14日
12月15日
平均气温(℃)
9
10
12
11
8
销量(杯)
23
25
30
26
21
(1)请根据所给五组数据,求出关于的线性回归方程;
(2)据(1)中所得的线性回归方程,若天气预报12月16日的白天平均气温7(℃),请预测该奶茶店这种饮料的销量. (参考公式:,)
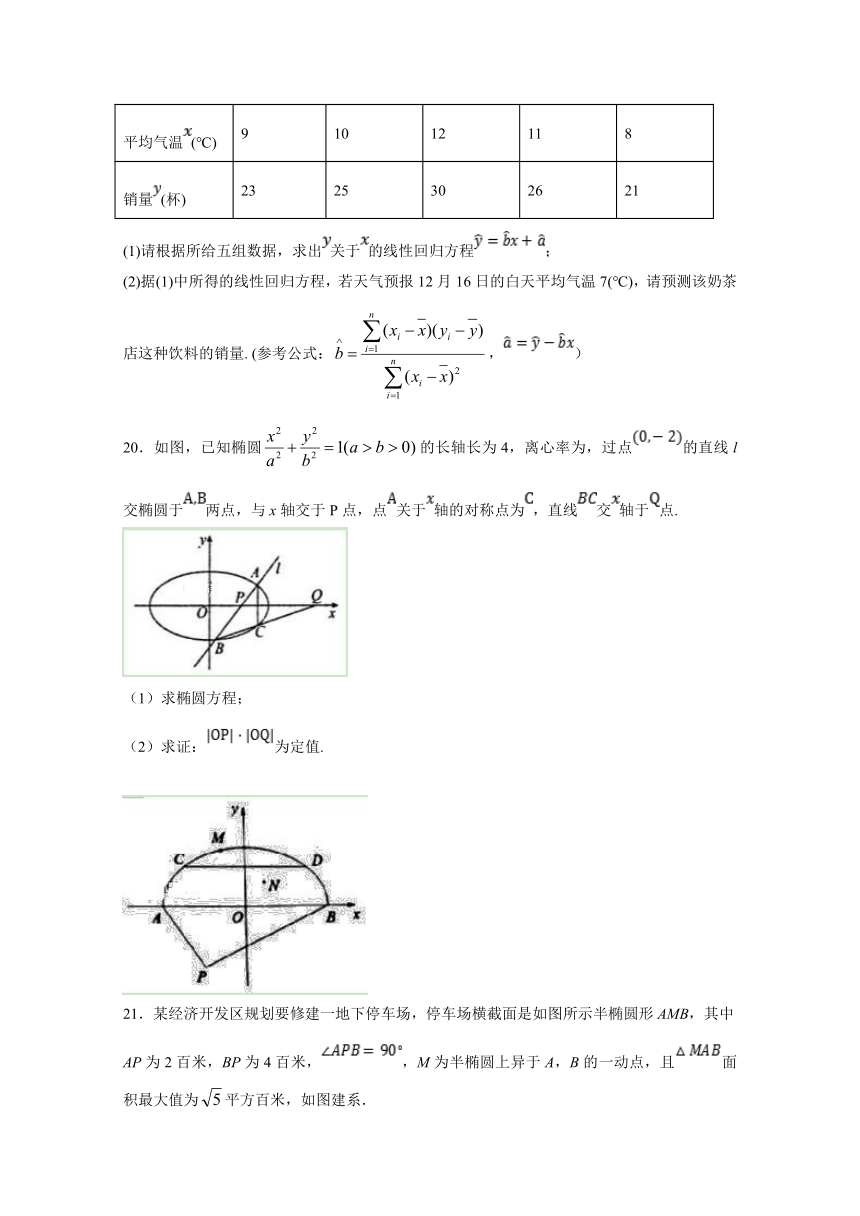
20.如图,已知椭圆的长轴长为4,离心率为,过点的直线l交椭圆于两点,与x轴交于P点,点关于轴的对称点为,直线交轴于点.
(1)求椭圆方程;
(2)求证:为定值.
21.某经济开发区规划要修建一地下停车场,停车场横截面是如图所示半椭圆形AMB,其中AP为2百米,BP为4百米,,M为半椭圆上异于A,B的一动点,且面积最大值为平方百米,如图建系.
求出半椭圆弧的方程;
若要将修建地下停车场挖出的土运到指定位置P处,N为运土点,以A,B为出口,要使运土最省工,工程部需要指定一条分界线,请求出分界线所在的曲线方程;
若在半椭圆形停车场的上方修建矩形商场,矩形的一边CD与AB平行,设百米,试确定t的值,使商场地面的面积最大.
22.已知椭圆的离心率为,分别为左,右焦点,分别为左,右顶点,D为上顶点,原点到直线的距离为.设点在第一象限,纵坐标为t,且轴,连接交椭圆于点.
(1)求椭圆的方程;
(2)(文)若三角形的面积等于四边形的面积,求直线的方程;
(理)求过点的圆方程(结果用t表示)
参考答案
1.D 2.D 3.A 4.C 5.C 6.A 7.C 8.D 9.B 10.A 11.C 12.B
13. 14. 15.< 16.6
17.(1); (2).
18.(1)(2)文:理:
19.解:
(1)由条件中的数据可得,,
,
.
∴,
∴.
∴关于的线性回归方程.
(2)由(1)可得,当时, .
∴预测该奶茶店这种饮料的销量大约为19杯.
20.解:(1)由题意得解得
所以椭圆方程为
(2)直线方程为,则的坐标为
设,,则,
直线方程为,令,得的横坐标为①
又得,得
代入①得
得
∴为常数4.
21.解:在直角三角形PAB中,,,
由勾股定理得:.
设椭圆方程为.
由题意得,解得,.
椭圆弧的方程为;
由点N到P的路程相等,,即.
得,在以A,B为焦点的双曲线上,
设双曲线方程为,
则,解得,.
双曲线方程为;
由,设,则.
商场地面积为.
,,
则.
当且仅当,即时“”成立.
当时,商场地面的面积最大为平方百米.
22.解:(1)因为椭圆的由离心率为,
所以,,所以直线的方程为,
又到直线的距离为,所以,
所以,,
所以椭圆的方程为.
(2)(文),,
直线的方程为,
由,整理得,
解得:,则点的坐标是,
因为三角形的面积等于四边形的面积,所以三角形的面积等于三角形的面积,
,
,
则,解得.
所以直线的方程为.
(理),,
直线的方程为,
由,整理得,
解得:,则点的坐标是,
因为,,,
所以的垂直平分线,
的垂直平分线为,
所以过三点的圆的圆心为,
则过三点的圆方程为 ,
即所求圆方程为 .
数学试卷
一、单选题(本大题共12小题,每小题5分,共60分)
1.下列判断中正确的是( )
A. “若,则有实数根”的逆命题是真命题
B. “”是“直线与直线平行”的充要条件
C. 命题“”是真命题
D. 命题“”在时是假命题
2.如图,等腰直角三角形的斜边长为,分别以三个顶点为圆心,1为半径在三角形内作圆弧,三段圆弧与斜边围成区域(图中阴影部分),若在此三角形内随机取一点,则此点取自区域的概率为
A. B. C. D.
(第2题图) (第3题图)
3.已知统计某校1000名学生的某次数学水平测试成绩得到样本频率分布直方图如图所示,则直方图中实数的值是
A. B. C. D.
4.双曲线C的中心在坐标原点O,右顶点,虚轴的上端点,虚轴下端点,左右焦点分别为、,直线与直线交于P点,若为锐角,则双曲线C的离心率的取值范围为
A. B. C. D.
5.若命题“”为假命题,则的取值范围是( )
A. B. C. D.
6. P是双曲线左支上的一点,F1、F2分别是左、右焦点,且焦距为2c,则的内切圆的圆心的横坐标为( )
(A) (B) (C) (D)
7.已知分别为椭圆的左右焦点,点在椭圆上,当时,则点横坐标的取值范围是( )
A. B. C. D.
8.一个算法的程序框图如图所示,若该程序输出的结果是,则判断框中应填入的条件是( )
A. B. C. D.
9.如图,已知椭圆的左,右焦点分别为,,是轴正半轴上一点,交椭圆于A,若,且的内切圆半径为,则椭圆的离心率为( )
A. B. C. D.
10.过双曲线的右焦点作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B,若,则双曲线的渐近线方程为( )
A. B. C. D.
11.采用系统抽样方法从人中抽取人做问卷调查,为此将他们随机编号为,,,,分组后某组抽到的号码为41.抽到的人中,编号落入区间 的人数为( )
A. 10 B. 1 C.12 D. 13
12.若点A,F分别是椭圆的左顶点和左焦点,过点F的直线交椭圆于M,N两点,记直线的斜率为,其满足,则直线的斜率为
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.某同学同时掷两颗均匀正方形骰子,得到的点数分别为,则椭圆的离心率的概率是__________.
14.椭圆的左、右焦点分别为,顶点到的距离为4,直线上存在点,使得为底角是的等腰三角形,则此椭圆方程为__________.
15.某校高中年级开设了丰富多彩的校本课程,甲、乙两班各随机抽取了5名学生的学分,用茎叶图表示(如右图).,分别表示甲、乙两班各自5名学生学分的标准差,则 .(填“”、“”或“=”)
16.已知是椭圆与双曲线的公共焦点,是它们的一个公共点,且,线段的垂直平分线过,若椭圆的离心率为,双曲线的离心率为,则的最小值为____________.
三、解答题(本大题共6小题,共70分,其中17题10分,其它题目每题12分)
17.已知命题,;命题:关于的方程有两个不同的实数根.
(1)若为真命题,求实数的取值范围;
(2)若为真命题,为假命题,求实数的取值范围.
已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为,右顶点为,
(1)求该椭圆的标准方程;
(2)(文)若是椭圆上的动点,过P作垂直于x轴的垂线,垂足为M,延长MP至N,使得P恰好为MN中点,求点N的轨迹方程;
(理)若已知点,是椭圆上的动点,求线段中点的轨迹方程;
19.某位同学进行社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了12月11日至12月15日的白天平均气温 (℃)与该小卖部的这种饮料销量(杯),得到如下数据:
日期
12月11日
12月12日
12月13日
12月14日
12月15日
平均气温(℃)
9
10
12
11
8
销量(杯)
23
25
30
26
21
(1)请根据所给五组数据,求出关于的线性回归方程;
(2)据(1)中所得的线性回归方程,若天气预报12月16日的白天平均气温7(℃),请预测该奶茶店这种饮料的销量. (参考公式:,)
20.如图,已知椭圆的长轴长为4,离心率为,过点的直线l交椭圆于两点,与x轴交于P点,点关于轴的对称点为,直线交轴于点.
(1)求椭圆方程;
(2)求证:为定值.
21.某经济开发区规划要修建一地下停车场,停车场横截面是如图所示半椭圆形AMB,其中AP为2百米,BP为4百米,,M为半椭圆上异于A,B的一动点,且面积最大值为平方百米,如图建系.
求出半椭圆弧的方程;
若要将修建地下停车场挖出的土运到指定位置P处,N为运土点,以A,B为出口,要使运土最省工,工程部需要指定一条分界线,请求出分界线所在的曲线方程;
若在半椭圆形停车场的上方修建矩形商场,矩形的一边CD与AB平行,设百米,试确定t的值,使商场地面的面积最大.
22.已知椭圆的离心率为,分别为左,右焦点,分别为左,右顶点,D为上顶点,原点到直线的距离为.设点在第一象限,纵坐标为t,且轴,连接交椭圆于点.
(1)求椭圆的方程;
(2)(文)若三角形的面积等于四边形的面积,求直线的方程;
(理)求过点的圆方程(结果用t表示)
参考答案
1.D 2.D 3.A 4.C 5.C 6.A 7.C 8.D 9.B 10.A 11.C 12.B
13. 14. 15.< 16.6
17.(1); (2).
18.(1)(2)文:理:
19.解:
(1)由条件中的数据可得,,
,
.
∴,
∴.
∴关于的线性回归方程.
(2)由(1)可得,当时, .
∴预测该奶茶店这种饮料的销量大约为19杯.
20.解:(1)由题意得解得
所以椭圆方程为
(2)直线方程为,则的坐标为
设,,则,
直线方程为,令,得的横坐标为①
又得,得
代入①得
得
∴为常数4.
21.解:在直角三角形PAB中,,,
由勾股定理得:.
设椭圆方程为.
由题意得,解得,.
椭圆弧的方程为;
由点N到P的路程相等,,即.
得,在以A,B为焦点的双曲线上,
设双曲线方程为,
则,解得,.
双曲线方程为;
由,设,则.
商场地面积为.
,,
则.
当且仅当,即时“”成立.
当时,商场地面的面积最大为平方百米.
22.解:(1)因为椭圆的由离心率为,
所以,,所以直线的方程为,
又到直线的距离为,所以,
所以,,
所以椭圆的方程为.
(2)(文),,
直线的方程为,
由,整理得,
解得:,则点的坐标是,
因为三角形的面积等于四边形的面积,所以三角形的面积等于三角形的面积,
,
,
则,解得.
所以直线的方程为.
(理),,
直线的方程为,
由,整理得,
解得:,则点的坐标是,
因为,,,
所以的垂直平分线,
的垂直平分线为,
所以过三点的圆的圆心为,
则过三点的圆方程为 ,
即所求圆方程为 .
同课章节目录
