第21章 二次函数与反比例函数单元测评卷(二)
文档属性
| 名称 | 第21章 二次函数与反比例函数单元测评卷(二) |

|
|
| 格式 | zip | ||
| 文件大小 | 213.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-25 00:00:00 | ||
图片预览


文档简介
第21章《二次函数与反比例函数》测评卷(二)
(时间:90分钟 满分:100分)
一、精心选一选(每小题3分,共36分)
1.以x为自变量的函数:①;②;③;④.是二次函数的有( ).
A.②③ B.②③④ C.①②③ D.①②③④
2.抛物线向右平移3个单位,所得的抛物线解析式为( ).
A. B.
C. D.
3.二次函数的最大值等于( ).
A. B. C. D.
4.抛物线与坐标轴的交点个数是( )
A.0 B.1 C.2 D.3
5.将抛物线先向右平移4个单位,再向上平移3个单位后,所得的抛物线解析式为
,则原抛物线的解析式是( ).
A. B.
C. D.
6.已知反比例函数的图像的两个分支分别位于第一、三象限,则m的值为( ).
A. B. C. D.
7.抛物线的对称轴是( ).
A. B. C. D.
8.抛物线的顶点坐标是( ).
A. B. C. D.
9.双曲线与直线交于点,则另一个交点的坐标是( ).
A. B. C. D.
10.如果A,B,C在函数的图像上,且,则的大小关系是( )
A . B. C. D.
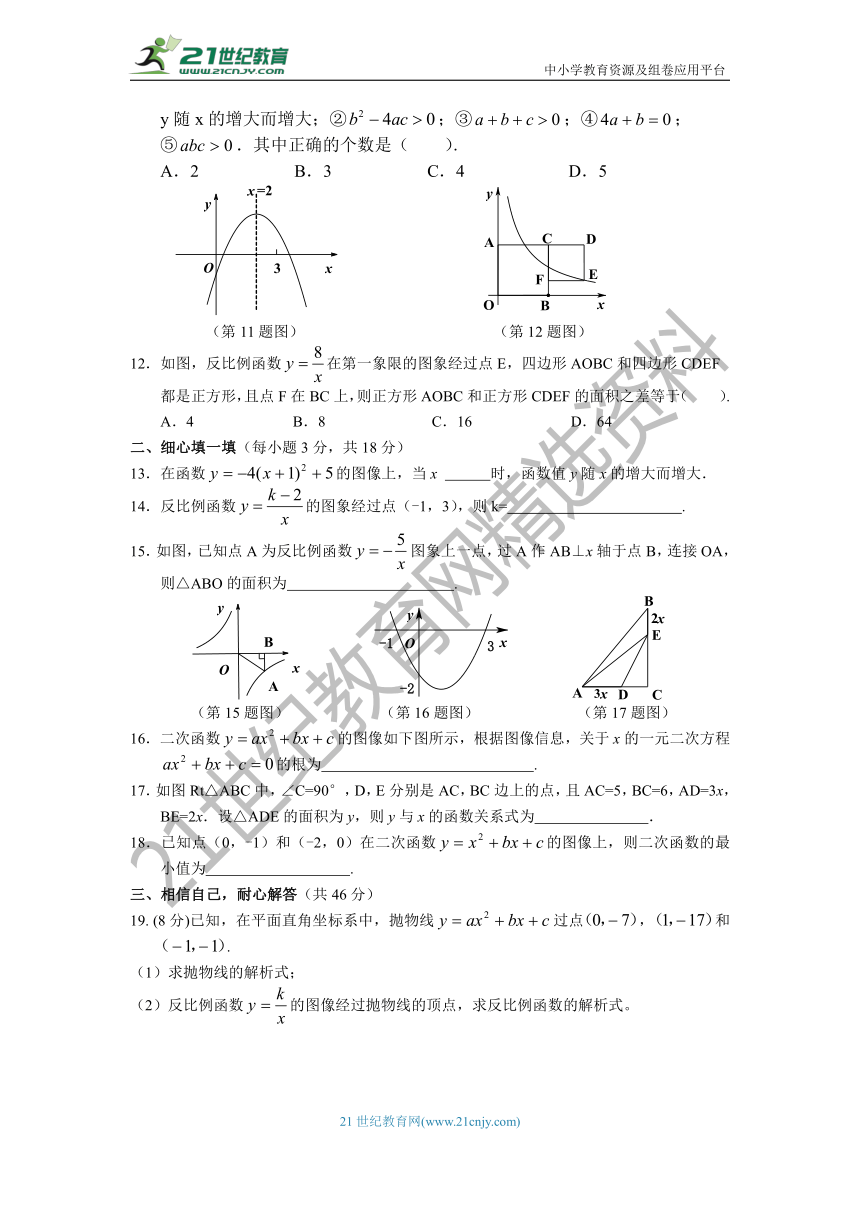
11.二次函数的图像如图所示,下列结论:①当时,y随x的增大而增大;②;③;④;
⑤.其中正确的个数是( ).
A.2 B.3 C.4 D.5
(第11题图) (第12题图)
12.如图,反比例函数在第一象限的图象经过点E,四边形AOBC和四边形CDEF都是正方形,且点F在BC上,则正方形AOBC和正方形CDEF的面积之差等于( ).
A.4 B.8 C.16 D.64
二、细心填一填(每小题3分,共18分)
13.在函数的图像上,当x 时,函数值y随x的增大而增大.
14.反比例函数的图象经过点(-1,3),则k= .
15.如图,已知点A为反比例函数图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为 .
(第15题图) (第16题图) (第17题图)
16.二次函数的图像如下图所示,根据图像信息,关于x的一元二次方程的根为 .
17.如图Rt△ABC中,∠C=90°,D,E分别是AC,BC边上的点,且AC=5,BC=6,AD=3x,BE=2x.设△ADE的面积为y,则y与x的函数关系式为 .
18.已知点(0,-1)和(-2,0)在二次函数的图像上,则二次函数的最小值为 .
三、相信自己,耐心解答(共46分)
19. (8分)已知,在平面直角坐标系中,抛物线过点,和.
(1)求抛物线的解析式;
(2)反比例函数的图像经过抛物线的顶点,求反比例函数的解析式。
20.(8分)某产品新投入市场,已知成本价是50元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
时间
第1天
第2天
第3天
第4天
售价x元
75
100
125
250
销售量y
20
15
12
6
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若该产品计划每天的销售利润为1000元,则其单价应定为多少元?
21.(9分)如图,某学生推铅球,铅球出手(点A处)的高度是,出手后的铅球沿一段抛物线运行,量得铅球落地点C与学生的水平距离OC=.
(1)求抛物线的解析式(注明x的取值范围);
(2)铅球运行中,最高是多少米?此时铅球与学生水平距离是多少米?
22.(10分)直线与反比例函数的图象在第一象限相交于点A,B两点,其中点A的坐标为(1,3),点B的横坐标为3.
(1)求直线的解析式;
(2)求△AOB的面积;
(3)在第一象限内,直接写出反比例函数值大于一次函数值的自变量x的取值范围.
23.(11分)如图,对称轴为直线的抛物线经过A(,0),C(0,2)两点,抛物线与轴的另一交点为B
(1)求抛物线的解析式;
(2)若点D为第一象限内抛物线上的一点,设四边形BDCO的面积为S,求S的最大值.
九上答案
第21章《二次函数与反比例函数》测评卷(二)答案
一、精心选一选(每小题3分,共36分)
1.C;2.D;3.C;4.D;5.B;6.B;7.A;8.B;9.D;10.D;11.C;12.B.
二、细心填一填(每小题3分,共18分)
13.;14.;15.;16.,;17.;18..
三、相信自己,耐心解答(共46分)
19. (8分)解:(1)依题意,得:
,解得:
∴
(2)抛物线的顶点坐标为.
∴,即.
∴
20.(8分)解:(1)xy=75×20=100×15=125×12=250×6=1500.
∴
(2)设单价应定为a元,则:
∴
答:单价应定为150元.
21.(9分)解:(1)把A(0,),C(10,0)代入待定解析式,得:
,解得:.
∴.
(2)当=4时,=3.
∴铅球运行中,最高是3米,此时铅球与学生水平距离4米.
22.(10分)解:(1)由经过点(1,3),得:
,
∴.
当时,,即B(3,1).
∴,解得:,.
∴.
(2)=.
(3)在第一象限内,0<或时,反比例函数值大于一次函数值.
23.(11分)解:(1)则抛物线的解析式为,则:
把A(,0),C(0,2)代入,得:
,解得:.
∴,即
(2)解,得:,.
∴B(4,0).
设D(x,y),则有:
∴ =6.
(时间:90分钟 满分:100分)
一、精心选一选(每小题3分,共36分)
1.以x为自变量的函数:①;②;③;④.是二次函数的有( ).
A.②③ B.②③④ C.①②③ D.①②③④
2.抛物线向右平移3个单位,所得的抛物线解析式为( ).
A. B.
C. D.
3.二次函数的最大值等于( ).
A. B. C. D.
4.抛物线与坐标轴的交点个数是( )
A.0 B.1 C.2 D.3
5.将抛物线先向右平移4个单位,再向上平移3个单位后,所得的抛物线解析式为
,则原抛物线的解析式是( ).
A. B.
C. D.
6.已知反比例函数的图像的两个分支分别位于第一、三象限,则m的值为( ).
A. B. C. D.
7.抛物线的对称轴是( ).
A. B. C. D.
8.抛物线的顶点坐标是( ).
A. B. C. D.
9.双曲线与直线交于点,则另一个交点的坐标是( ).
A. B. C. D.
10.如果A,B,C在函数的图像上,且,则的大小关系是( )
A . B. C. D.
11.二次函数的图像如图所示,下列结论:①当时,y随x的增大而增大;②;③;④;
⑤.其中正确的个数是( ).
A.2 B.3 C.4 D.5
(第11题图) (第12题图)
12.如图,反比例函数在第一象限的图象经过点E,四边形AOBC和四边形CDEF都是正方形,且点F在BC上,则正方形AOBC和正方形CDEF的面积之差等于( ).
A.4 B.8 C.16 D.64
二、细心填一填(每小题3分,共18分)
13.在函数的图像上,当x 时,函数值y随x的增大而增大.
14.反比例函数的图象经过点(-1,3),则k= .
15.如图,已知点A为反比例函数图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为 .
(第15题图) (第16题图) (第17题图)
16.二次函数的图像如下图所示,根据图像信息,关于x的一元二次方程的根为 .
17.如图Rt△ABC中,∠C=90°,D,E分别是AC,BC边上的点,且AC=5,BC=6,AD=3x,BE=2x.设△ADE的面积为y,则y与x的函数关系式为 .
18.已知点(0,-1)和(-2,0)在二次函数的图像上,则二次函数的最小值为 .
三、相信自己,耐心解答(共46分)
19. (8分)已知,在平面直角坐标系中,抛物线过点,和.
(1)求抛物线的解析式;
(2)反比例函数的图像经过抛物线的顶点,求反比例函数的解析式。
20.(8分)某产品新投入市场,已知成本价是50元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
时间
第1天
第2天
第3天
第4天
售价x元
75
100
125
250
销售量y
20
15
12
6
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若该产品计划每天的销售利润为1000元,则其单价应定为多少元?
21.(9分)如图,某学生推铅球,铅球出手(点A处)的高度是,出手后的铅球沿一段抛物线运行,量得铅球落地点C与学生的水平距离OC=.
(1)求抛物线的解析式(注明x的取值范围);
(2)铅球运行中,最高是多少米?此时铅球与学生水平距离是多少米?
22.(10分)直线与反比例函数的图象在第一象限相交于点A,B两点,其中点A的坐标为(1,3),点B的横坐标为3.
(1)求直线的解析式;
(2)求△AOB的面积;
(3)在第一象限内,直接写出反比例函数值大于一次函数值的自变量x的取值范围.
23.(11分)如图,对称轴为直线的抛物线经过A(,0),C(0,2)两点,抛物线与轴的另一交点为B
(1)求抛物线的解析式;
(2)若点D为第一象限内抛物线上的一点,设四边形BDCO的面积为S,求S的最大值.
九上答案
第21章《二次函数与反比例函数》测评卷(二)答案
一、精心选一选(每小题3分,共36分)
1.C;2.D;3.C;4.D;5.B;6.B;7.A;8.B;9.D;10.D;11.C;12.B.
二、细心填一填(每小题3分,共18分)
13.;14.;15.;16.,;17.;18..
三、相信自己,耐心解答(共46分)
19. (8分)解:(1)依题意,得:
,解得:
∴
(2)抛物线的顶点坐标为.
∴,即.
∴
20.(8分)解:(1)xy=75×20=100×15=125×12=250×6=1500.
∴
(2)设单价应定为a元,则:
∴
答:单价应定为150元.
21.(9分)解:(1)把A(0,),C(10,0)代入待定解析式,得:
,解得:.
∴.
(2)当=4时,=3.
∴铅球运行中,最高是3米,此时铅球与学生水平距离4米.
22.(10分)解:(1)由经过点(1,3),得:
,
∴.
当时,,即B(3,1).
∴,解得:,.
∴.
(2)=.
(3)在第一象限内,0<或时,反比例函数值大于一次函数值.
23.(11分)解:(1)则抛物线的解析式为,则:
把A(,0),C(0,2)代入,得:
,解得:.
∴,即
(2)解,得:,.
∴B(4,0).
设D(x,y),则有:
∴ =6.
