第21章 二次函数与反比例函数单元测评卷(一)
文档属性
| 名称 | 第21章 二次函数与反比例函数单元测评卷(一) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-25 20:57:49 | ||
图片预览



文档简介
第21章《二次函数与反比例函数》测评卷(一)
(时间:90分钟 满分:100分)
一、精心选一选(每小题3分,共36分)
1.在下列表达式中,x为自变量,则是二次函数的是( ).
A. B. C. D.
2.抛物线的对称轴是( ).
A. B. C. D.
3.抛物线的对称轴是( ).
A. B. C. D.
4.二次函数的最小值是 ( ).
A. B. C. D.
5.抛物线的顶点坐标是( ).
A.(3,1) B.(-3,1) C.(0,1) D.(0,-1)
6.抛物线向下平移2个单位,所得的抛物线解析式为( ).
A. B.
C. D.
7.如上图,过反比例函数(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=3,则k的值为( ).21·cn·jy·com21cnjy.com
A.3 B.4 C.5 D.6
8.已知函数是自变量为x的反比例函数,则m的值为( ).
A. B. C. D.
9.已知反比例函数(a≠0)图像的两个分支分别位于第二、四象限,则二次函数的图像可能是( ).21世纪教育网21-cn-jy.com21教育网
A B C D
10.将二次函数配成的形式,正确的是( ).
A. B.
C. D.
11.抛物线向左平移3个单位,所得的抛物线解析式为( ).
A. B.
C. D.
12.已知关于x的一元二次方程(a>0)的两个根分别是,.当二次函数的函数值大于0时, 则x的取值范围是( ).
A . B. C. D .
二、细心填一填(每小题3分,共18分)
13.写出一个经过点(-1,0)的二次函数: .
14.抛物线经过点(-3,1),则抛物线的开口方向是 .
15.反比例函数的图像与直线交于两点,则这两点的坐标分别是( , ) 和( , ).21世纪21世纪教育网有21·cn·jy·com
16.某同学踢出的足球高度y米与水平距离x米之间的函数关系式为,则足球的落地点与这位同学踢出足球点的距离是 .
17.抛物线与x轴只有一个交点,则k的值为 .
18.如右图,已知点A(5,2),过点A作AB⊥x轴于点B,AC⊥y轴
于点C,反比例函数的图象交AB于点D,交AC于点E.
如果四边形ODAE的面积为7,则k= .
三、相信自己,耐心解答(共46分)
19.(6分)如下图,M在反比例函数的图象上,且点M到点x轴,y轴的距离都等于,求反比例函数的解析式.21cnjy.comwww.21-cn-jy.com
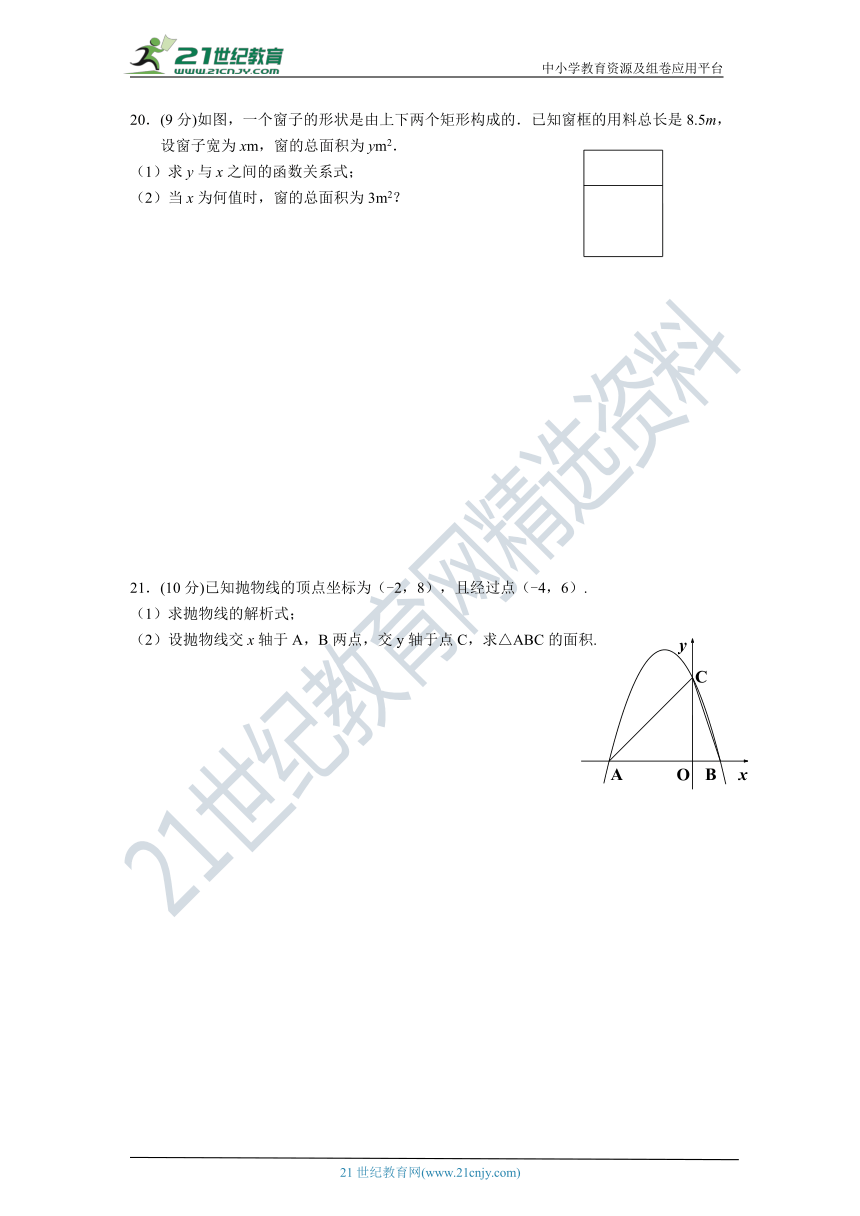
20.(9分)如图,一个窗子的形状是由上下两个矩形构成的.已知窗框的用料总长是8.5m,设窗子宽为xm,窗的总面积为ym2.2·1·c·n·j·y2·1·c·n·j·y
(1)求y与x之间的函数关系式;
(2)当x为何值时,窗的总面积为3m2?
21.(10分)已知抛物线的顶点坐标为(-2,8),且经过点(-4,6).
(1)求抛物线的解析式;
(2)设抛物线交x轴于A,B两点,交y轴于点C,求△ABC的面积.
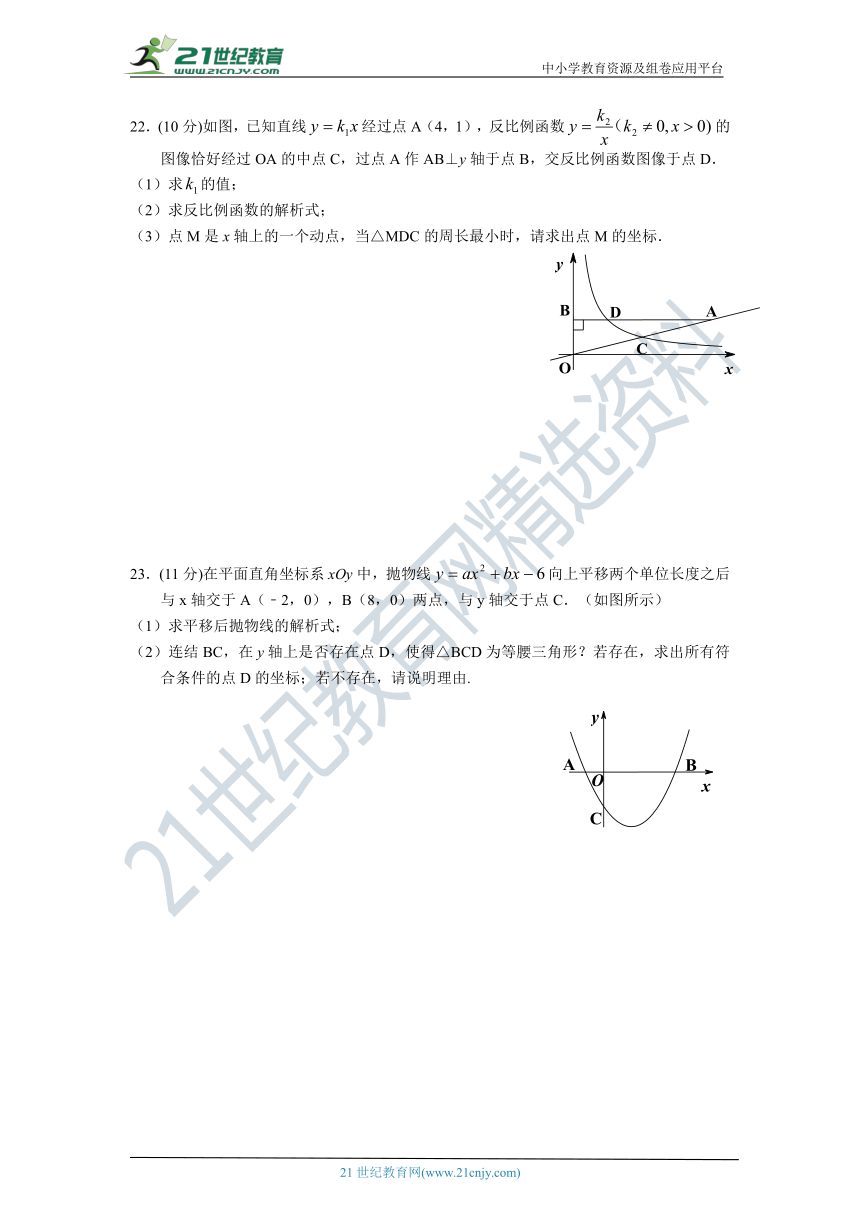
22.(10分)如图,已知直线经过点A(4,1),反比例函数的图像恰好经过OA的中点C,过点A作AB⊥y轴于点B,交反比例函数图像于点D.
(1)求的值;
(2)求反比例函数的解析式;
(3)点M是x轴上的一个动点,当△MDC的周长最小时,请求出点M的坐标.
23.(11分)在平面直角坐标系xOy中,抛物线向上平移两个单位长度之后与x轴交于A(﹣2,0),B(8,0)两点,与y轴交于点C.(如图所示)
(1)求平移后抛物线的解析式;
(2)连结BC,在y轴上是否存在点D,使得△BCD为等腰三角形?若存在,求出所有符合条件的点D的坐标;若不存在,请说明理由. 21教育网21世纪教育网版权所有
九上答案
第21章《二次函数与反比例函数》测评卷(一)答案
一、精心选一选(每小题3分,共36分)
1.D;2.C;3.B;4.D;5.C;6. B;7.D;8.B;9.C;10.A;11.A;12.B.
二、细心填一填(每小题3分,共18分)
13.(不唯一);14.向下;15.(-2,-1)和(1,2);16.20;17.2;18.3.
三、相信自己,耐心解答(共46分)
19. (6分)解:如图所示,k<0.所以=-k.
∴,即.
∴.
20.(9分)解:(1)根据题意,得:
=.
(2)根据题意,得:
=3
整理,得:
解得:
,.
所以,当等于或时,窗的总面积为3m2.
21.(10分)解:(1)设抛物线的解析式为,则:
.
把(-4,6)代入,得:
∴ .
∴.
(2)当时,=6;
当时,,解得:.
∴A(,0),B(2,0),C(0,6).
∴=24.
22.(10分)解:(1)依题意,得:,
∴.
(2)由 A(4,1),C为OA的中点,得:C(2,).
∴,即.
∴.
(3)当时,,即.
∴D(1,1),
设与D关于x轴对称,则(1,).
设直线的解析式为,得:
,解得:.
∴直线的解析式为.
当时,,解得:.
∴.
23.(11分)解:(1)设平移后的抛物线解析式为,则:
,
解得:.
∴平移后的抛物线解析式为.
(2)当时,,即C(0,).
当时,,解得:.
∴B(8,0),
∴BC= =,
∴在y轴上存在四点D使△BCD为等腰三角形:
(0,4),(0,),(0,),(0,6).
(时间:90分钟 满分:100分)
一、精心选一选(每小题3分,共36分)
1.在下列表达式中,x为自变量,则是二次函数的是( ).
A. B. C. D.
2.抛物线的对称轴是( ).
A. B. C. D.
3.抛物线的对称轴是( ).
A. B. C. D.
4.二次函数的最小值是 ( ).
A. B. C. D.
5.抛物线的顶点坐标是( ).
A.(3,1) B.(-3,1) C.(0,1) D.(0,-1)
6.抛物线向下平移2个单位,所得的抛物线解析式为( ).
A. B.
C. D.
7.如上图,过反比例函数(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=3,则k的值为( ).21·cn·jy·com21cnjy.com
A.3 B.4 C.5 D.6
8.已知函数是自变量为x的反比例函数,则m的值为( ).
A. B. C. D.
9.已知反比例函数(a≠0)图像的两个分支分别位于第二、四象限,则二次函数的图像可能是( ).21世纪教育网21-cn-jy.com21教育网
A B C D
10.将二次函数配成的形式,正确的是( ).
A. B.
C. D.
11.抛物线向左平移3个单位,所得的抛物线解析式为( ).
A. B.
C. D.
12.已知关于x的一元二次方程(a>0)的两个根分别是,.当二次函数的函数值大于0时, 则x的取值范围是( ).
A . B. C. D .
二、细心填一填(每小题3分,共18分)
13.写出一个经过点(-1,0)的二次函数: .
14.抛物线经过点(-3,1),则抛物线的开口方向是 .
15.反比例函数的图像与直线交于两点,则这两点的坐标分别是( , ) 和( , ).21世纪21世纪教育网有21·cn·jy·com
16.某同学踢出的足球高度y米与水平距离x米之间的函数关系式为,则足球的落地点与这位同学踢出足球点的距离是 .
17.抛物线与x轴只有一个交点,则k的值为 .
18.如右图,已知点A(5,2),过点A作AB⊥x轴于点B,AC⊥y轴
于点C,反比例函数的图象交AB于点D,交AC于点E.
如果四边形ODAE的面积为7,则k= .
三、相信自己,耐心解答(共46分)
19.(6分)如下图,M在反比例函数的图象上,且点M到点x轴,y轴的距离都等于,求反比例函数的解析式.21cnjy.comwww.21-cn-jy.com
20.(9分)如图,一个窗子的形状是由上下两个矩形构成的.已知窗框的用料总长是8.5m,设窗子宽为xm,窗的总面积为ym2.2·1·c·n·j·y2·1·c·n·j·y
(1)求y与x之间的函数关系式;
(2)当x为何值时,窗的总面积为3m2?
21.(10分)已知抛物线的顶点坐标为(-2,8),且经过点(-4,6).
(1)求抛物线的解析式;
(2)设抛物线交x轴于A,B两点,交y轴于点C,求△ABC的面积.
22.(10分)如图,已知直线经过点A(4,1),反比例函数的图像恰好经过OA的中点C,过点A作AB⊥y轴于点B,交反比例函数图像于点D.
(1)求的值;
(2)求反比例函数的解析式;
(3)点M是x轴上的一个动点,当△MDC的周长最小时,请求出点M的坐标.
23.(11分)在平面直角坐标系xOy中,抛物线向上平移两个单位长度之后与x轴交于A(﹣2,0),B(8,0)两点,与y轴交于点C.(如图所示)
(1)求平移后抛物线的解析式;
(2)连结BC,在y轴上是否存在点D,使得△BCD为等腰三角形?若存在,求出所有符合条件的点D的坐标;若不存在,请说明理由. 21教育网21世纪教育网版权所有
九上答案
第21章《二次函数与反比例函数》测评卷(一)答案
一、精心选一选(每小题3分,共36分)
1.D;2.C;3.B;4.D;5.C;6. B;7.D;8.B;9.C;10.A;11.A;12.B.
二、细心填一填(每小题3分,共18分)
13.(不唯一);14.向下;15.(-2,-1)和(1,2);16.20;17.2;18.3.
三、相信自己,耐心解答(共46分)
19. (6分)解:如图所示,k<0.所以=-k.
∴,即.
∴.
20.(9分)解:(1)根据题意,得:
=.
(2)根据题意,得:
=3
整理,得:
解得:
,.
所以,当等于或时,窗的总面积为3m2.
21.(10分)解:(1)设抛物线的解析式为,则:
.
把(-4,6)代入,得:
∴ .
∴.
(2)当时,=6;
当时,,解得:.
∴A(,0),B(2,0),C(0,6).
∴=24.
22.(10分)解:(1)依题意,得:,
∴.
(2)由 A(4,1),C为OA的中点,得:C(2,).
∴,即.
∴.
(3)当时,,即.
∴D(1,1),
设与D关于x轴对称,则(1,).
设直线的解析式为,得:
,解得:.
∴直线的解析式为.
当时,,解得:.
∴.
23.(11分)解:(1)设平移后的抛物线解析式为,则:
,
解得:.
∴平移后的抛物线解析式为.
(2)当时,,即C(0,).
当时,,解得:.
∴B(8,0),
∴BC= =,
∴在y轴上存在四点D使△BCD为等腰三角形:
(0,4),(0,),(0,),(0,6).
