第23章 解直角三角形单元测评卷(二)
文档属性
| 名称 | 第23章 解直角三角形单元测评卷(二) |  | |
| 格式 | zip | ||
| 文件大小 | 269.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-25 21:34:54 | ||
图片预览

文档简介
第23章《解直角三角形》测评卷(二)
(时间:90分钟 满分:100分)
一、精心选一选(每小题3分,共36分)
1.的值等于( ).
A.1 B. C. D.
2.Rt△ABC中,∠C=90°,,则的值等于( ).
A. B. C. D.
3.在中,是斜边上的中线,,,则 的值是( ).
A. B. C. D.
4.张乐同学遇到了这样一道题:tan(α+20°)=1,你猜想锐角α的度数应是( ).
A.40° B.30° C.20° D.10°
5.如图,在Rt△ABC中,∠C=90°,∠A=36°,AB=2,则下列结论中错误的是( ).
A.AC=2tan54° B.∠B=54° C.BC=2sin36° D.AC=2cos36°
(第5题图) (第6题图) (第7题图)
6.如图,两条宽度都是40 m的公路相交成α角,那么这两条公路相交处公共部分(图中阴影部分)的路面面积是( ).
A.(m2) B.(m2) C.1600sinα(m2) D.1600cosα(m2)
7.如图,在矩形ABCD中,DE⊥AC于E, cos∠ADE =,AB=4,则AD等于( ).
A.3 B. C. D.
8.身高相同的三个小朋友甲、乙、丙一起放风筝,他们放出的线长分别为300 m,250 m,200 m;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝( ).
A.甲的最高 B.乙的最低 C.丙的最低 D.乙的最高
9.?某人在斜坡上走了26米,上升的高度为10米,那么这个斜坡的坡度i =( ).
A. B. C. D.
10.已知在△ABC中,∠C=90°,sinA=,那么tan(90°-A)的值等于( )
A. B. C. D.1
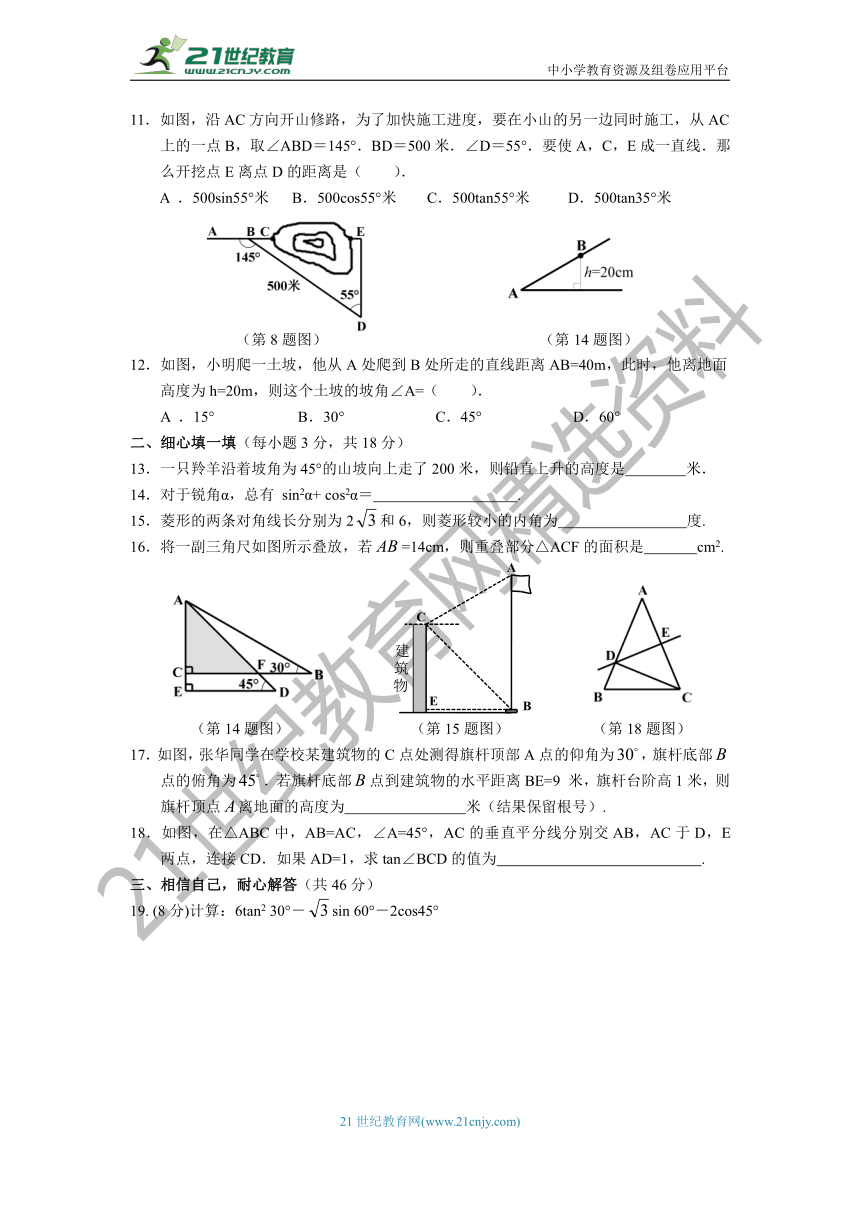
11.如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=145°.BD=500米.∠D=55°.要使A,C,E成一直线.那么开挖点E离点D的距离是( ).
A .500sin55°米 B.500cos55°米 C.500tan55°米 D.500tan35°米
(第8题图) (第14题图)
12.如图,小明爬一土坡,他从A处爬到B处所走的直线距离AB=40m,此时,他离地面高度为h=20m,则这个土坡的坡角∠A=( ).
A .15° B.30° C.45° D.60°
二、细心填一填(每小题3分,共18分)
13.一只羚羊沿着坡角为45°的山坡向上走了200米,则铅直上升的高度是 米.
14.对于锐角α,总有 sin2α+ cos2α= .
15.菱形的两条对角线长分别为2和6,则菱形较小的内角为 度.
16.将一副三角尺如图所示叠放,若=14cm,则重叠部分△ACF的面积是 cm2.
(第14题图) (第15题图) (第18题图)
17.如图,张华同学在学校某建筑物的C点处测得旗杆顶部A点的仰角为,旗杆底部 点的俯角为.若旗杆底部点到建筑物的水平距离BE=9 米,旗杆台阶高1米,则旗杆顶点离地面的高度为 米(结果保留根号).
18.如图,在△ABC中,AB=AC,∠A=45°,AC的垂直平分线分别交AB,AC于D,E两点,连接CD.如果AD=1,求tan∠BCD的值为 .
三、相信自己,耐心解答(共46分)
19. (8分)计算:6tan2 30°-sin 60°-2cos45°
20.(9分)在Rt△中,,,,求△的周长和面积的值.
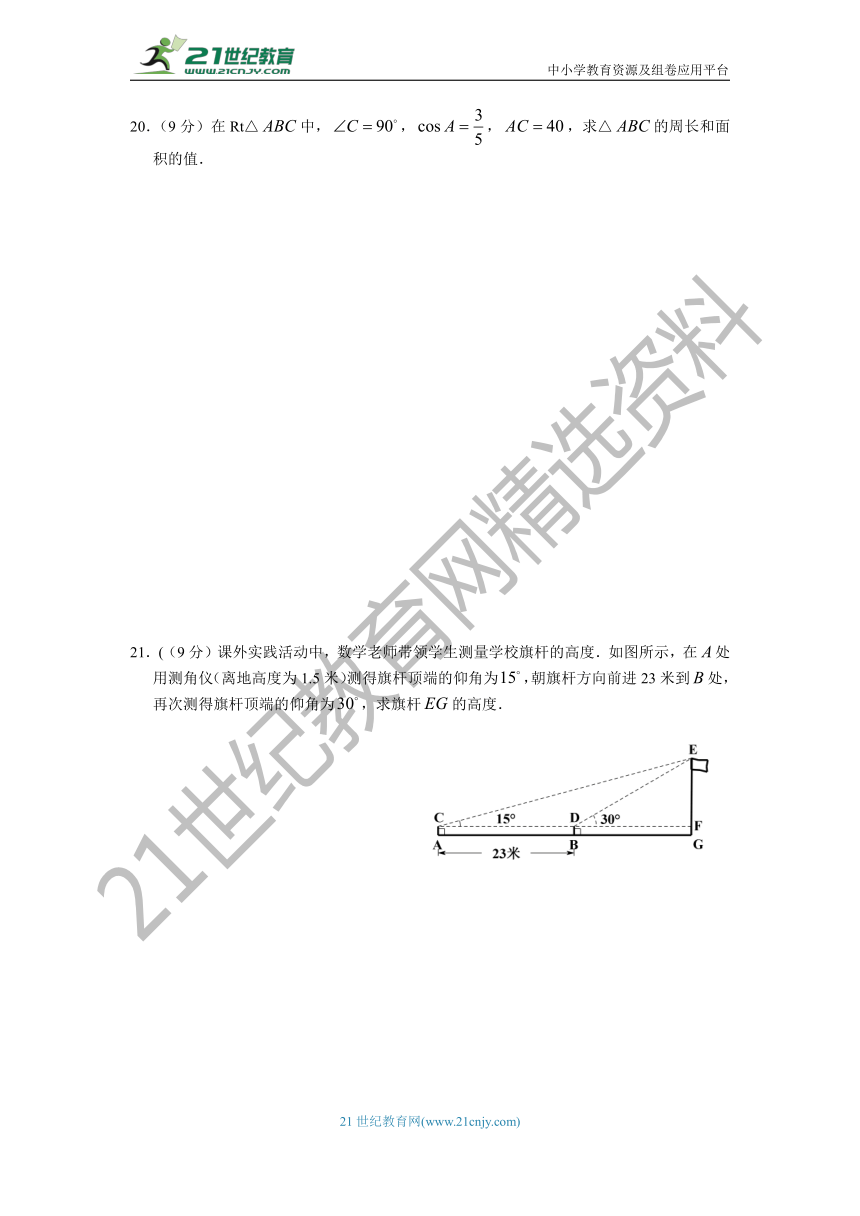
21.((9分)课外实践活动中,数学老师带领学生测量学校旗杆的高度.如图所示,在处用测角仪(离地高度为1.5米)测得旗杆顶端的仰角为,朝旗杆方向前进23米到处,再次测得旗杆顶端的仰角为,求旗杆的高度.
22.(10分)“为了安全,请勿超速”.如图所示,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)
23.(10分)如图,要在宽为22米的某大道AB两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120o角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直.当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC的高度应设计为多少米?
九上答案
第23章《解直角三角形》测评卷(二)答案
一、精心选一选(每小题3分,共36分)
1.B;2.B;3.C;4.D;5.A;6.C;7.C;8.D;9.C;10.B;11.B;12.B.
二、细心填一填(每小题3分,共18分)
13.100;14.1;15.60°;16.;17.;18..
三、相信自己,耐心解答(共46分)
19.
20.解:依题意,得:
==,
∴,
∴△的周长为:;
面积为:.
21.解:由题设可知,,
∴DE=CD=23(米).
在中,,
∴EF=DE=11.5(米),
∴EG=EF+GF=11.5+1.5=13(米).
∴旗杆的高度为13米.
22.解:此车没有超速.理由如下:
过C作CH⊥MN,
∵∠CBN=60°,BC=200米,
∴CH=BC?sin60°=200×=100(米),
BH=BC?cos60°=100(米),
∵∠CAN=45°,∴AH=CH=100米,
∴AB=100100
∵(100100)米/5秒=72(1)千米/小时
≈52.7千米/小时<60千米/小时,
∴此车没有超速.
23.解:延长OD,交BC的延长线于P.
∵∠ODC=∠B=90°,∠BCD=120°,
∴∠PCD=60°,
∴∠P=30°,
∵OB=11米,CD=2米,
∴PC=2÷sin30°=2÷=4米,
PB=BO÷tan30°=米,
∴BC=PB﹣PC=米.
(时间:90分钟 满分:100分)
一、精心选一选(每小题3分,共36分)
1.的值等于( ).
A.1 B. C. D.
2.Rt△ABC中,∠C=90°,,则的值等于( ).
A. B. C. D.
3.在中,是斜边上的中线,,,则 的值是( ).
A. B. C. D.
4.张乐同学遇到了这样一道题:tan(α+20°)=1,你猜想锐角α的度数应是( ).
A.40° B.30° C.20° D.10°
5.如图,在Rt△ABC中,∠C=90°,∠A=36°,AB=2,则下列结论中错误的是( ).
A.AC=2tan54° B.∠B=54° C.BC=2sin36° D.AC=2cos36°
(第5题图) (第6题图) (第7题图)
6.如图,两条宽度都是40 m的公路相交成α角,那么这两条公路相交处公共部分(图中阴影部分)的路面面积是( ).
A.(m2) B.(m2) C.1600sinα(m2) D.1600cosα(m2)
7.如图,在矩形ABCD中,DE⊥AC于E, cos∠ADE =,AB=4,则AD等于( ).
A.3 B. C. D.
8.身高相同的三个小朋友甲、乙、丙一起放风筝,他们放出的线长分别为300 m,250 m,200 m;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝( ).
A.甲的最高 B.乙的最低 C.丙的最低 D.乙的最高
9.?某人在斜坡上走了26米,上升的高度为10米,那么这个斜坡的坡度i =( ).
A. B. C. D.
10.已知在△ABC中,∠C=90°,sinA=,那么tan(90°-A)的值等于( )
A. B. C. D.1
11.如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=145°.BD=500米.∠D=55°.要使A,C,E成一直线.那么开挖点E离点D的距离是( ).
A .500sin55°米 B.500cos55°米 C.500tan55°米 D.500tan35°米
(第8题图) (第14题图)
12.如图,小明爬一土坡,他从A处爬到B处所走的直线距离AB=40m,此时,他离地面高度为h=20m,则这个土坡的坡角∠A=( ).
A .15° B.30° C.45° D.60°
二、细心填一填(每小题3分,共18分)
13.一只羚羊沿着坡角为45°的山坡向上走了200米,则铅直上升的高度是 米.
14.对于锐角α,总有 sin2α+ cos2α= .
15.菱形的两条对角线长分别为2和6,则菱形较小的内角为 度.
16.将一副三角尺如图所示叠放,若=14cm,则重叠部分△ACF的面积是 cm2.
(第14题图) (第15题图) (第18题图)
17.如图,张华同学在学校某建筑物的C点处测得旗杆顶部A点的仰角为,旗杆底部 点的俯角为.若旗杆底部点到建筑物的水平距离BE=9 米,旗杆台阶高1米,则旗杆顶点离地面的高度为 米(结果保留根号).
18.如图,在△ABC中,AB=AC,∠A=45°,AC的垂直平分线分别交AB,AC于D,E两点,连接CD.如果AD=1,求tan∠BCD的值为 .
三、相信自己,耐心解答(共46分)
19. (8分)计算:6tan2 30°-sin 60°-2cos45°
20.(9分)在Rt△中,,,,求△的周长和面积的值.
21.((9分)课外实践活动中,数学老师带领学生测量学校旗杆的高度.如图所示,在处用测角仪(离地高度为1.5米)测得旗杆顶端的仰角为,朝旗杆方向前进23米到处,再次测得旗杆顶端的仰角为,求旗杆的高度.
22.(10分)“为了安全,请勿超速”.如图所示,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)
23.(10分)如图,要在宽为22米的某大道AB两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120o角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直.当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC的高度应设计为多少米?
九上答案
第23章《解直角三角形》测评卷(二)答案
一、精心选一选(每小题3分,共36分)
1.B;2.B;3.C;4.D;5.A;6.C;7.C;8.D;9.C;10.B;11.B;12.B.
二、细心填一填(每小题3分,共18分)
13.100;14.1;15.60°;16.;17.;18..
三、相信自己,耐心解答(共46分)
19.
20.解:依题意,得:
==,
∴,
∴△的周长为:;
面积为:.
21.解:由题设可知,,
∴DE=CD=23(米).
在中,,
∴EF=DE=11.5(米),
∴EG=EF+GF=11.5+1.5=13(米).
∴旗杆的高度为13米.
22.解:此车没有超速.理由如下:
过C作CH⊥MN,
∵∠CBN=60°,BC=200米,
∴CH=BC?sin60°=200×=100(米),
BH=BC?cos60°=100(米),
∵∠CAN=45°,∴AH=CH=100米,
∴AB=100100
∵(100100)米/5秒=72(1)千米/小时
≈52.7千米/小时<60千米/小时,
∴此车没有超速.
23.解:延长OD,交BC的延长线于P.
∵∠ODC=∠B=90°,∠BCD=120°,
∴∠PCD=60°,
∴∠P=30°,
∵OB=11米,CD=2米,
∴PC=2÷sin30°=2÷=4米,
PB=BO÷tan30°=米,
∴BC=PB﹣PC=米.
