2018_2019高中数学第3章导数及其应用3.1.2瞬时变化率——导数(一)课件苏教版选修1_1(26张PPT)
文档属性
| 名称 | 2018_2019高中数学第3章导数及其应用3.1.2瞬时变化率——导数(一)课件苏教版选修1_1(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 00:00:00 | ||
图片预览








文档简介
课件26张PPT。3.1.2 瞬时变化率——导数(一)第3章 §3.1 导数的概念学习目标1.了解曲线的切线的概念,会用逼近的思想求切线斜率.
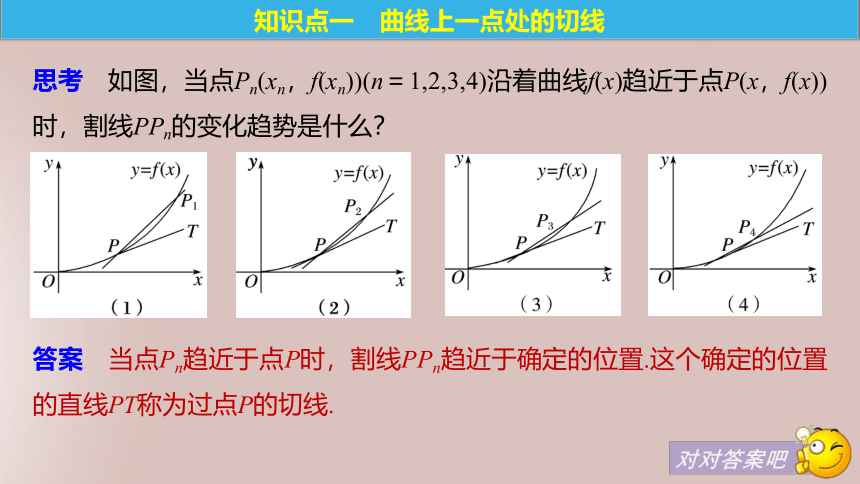
2.会求物体运动的瞬时速度与瞬时加速度.问题导学达标检测题型探究内容索引问题导学知识点一 曲线上一点处的切线思考 如图,当点Pn(xn,f(xn))(n=1,2,3,4)沿着曲线f(x)趋近于点P(x,f(x))时,割线PPn的变化趋势是什么?答案 当点Pn趋近于点P时,割线PPn趋近于确定的位置.这个确定的位置的直线PT称为过点P的切线.斜率梳理 可以用逼近的方法来计算切线的斜率,
设P(x,f(x)),Q(x+Δx,f(x+Δx)),当Δx无限趋近于0时, 无限趋近于点P(x,f(x))处的切线的
.知识点二 瞬时速度与瞬时加速度思考 瞬时速度和瞬时加速度和函数的变化率有什么关系?
答案 瞬时速度是位移对于时间的瞬时变化率,瞬时加速度是速度对于时间的瞬时变化率.梳理 (1)如果当Δt无限趋近于0时,运动物体位移S(t)的平均变化率
无限趋近于一个常数,那么这个常数称为物体在t=t0时的 ,即位移对于时间的 .(2)如果当Δt无限趋近于0时,运动物体速度v(t)的平均变化率
无限趋近于一个常数,那么这个常数称为物体在t=t0时的 ,即速度对于时间的 .瞬时速度瞬时变化率瞬时加速度瞬时变化率1.曲线上给定一点P,过点P可以作该曲线的两条割线.( )
2.过曲线上任一点可能作不出一条切线.( )
3.有的曲线过它上面的某一点可作两条切线.( )
4.平均速度刻画运动物体在某一时间段内变化的快慢程度,瞬时速度刻画物体在某一时刻变化的快慢程度.( )[思考辨析 判断正误]√×√√题型探究类型一 求曲线在某点处的切线斜率解答(1)点P处的切线的斜率;即点P处的切线的斜率为22=4.解答即12x-3y-16=0.(2)点P处的切线方程.反思与感悟 解决此类问题的关键是理解割线逼近切线的思想.即求曲线上一点处切线的斜率时,先表示出曲线在该点处的割线的斜率,则当Δx无限趋近于0时,可得到割线的斜率逼近切线的斜率.跟踪训练1 利用割线逼近切线的方法分别求曲线y=2x2在x=0,x=-1,x=2处的切线斜率.当Δx无限趋近于0时,kPQ无限趋近于4x0,从而曲线y=f(x)在x=0,x=-1,x=2处的切线斜率分别为0,-4,8.解答解 设P(x0,f(x0)),Q(x0+Δx,f(x0+Δx)),类型二 求瞬时速度、瞬时加速度解答例2 已知质点M的运动速度与运动时间的关系为v=3t2+2(速度单位:cm/s,时间单位:s),
(1)当t=2,Δt=0.01时,求 ;解答(2)求质点M在t=2 s时的瞬时加速度.解 当Δt无限趋近于0时,6t+3Δt无限趋近于6t,则质点M在t=2 s时的瞬时加速度为12 cm/s2.反思与感悟 (1)求瞬时速度的关键在于正确表示“位移的增量与时间增量的比值”,求瞬时加速度的关键在于正确表示“速度的增量与时间增量的比值”,注意二者的区别.
(2)求瞬时加速度:①求平均加速度 ;②令Δt→0,求出瞬时加速度.跟踪训练2 质点M按规律S(t)=at2+1做直线运动(位移单位:m,时间单位:s).若质点M在t=2 s时的瞬时速度为8 m/s,求常数a的值.解答解 ∵ΔS=S(2+Δt)-S(2)
=a(2+Δt)2+1-a·22-1=4aΔt+a(Δt)2,当Δt无限趋近于0时,4a+aΔt无限趋近于4a.
∵在t=2 s时,瞬时速度为8 m/s,
∴4a=8,∴a=2.达标检测答案12345解析1.已知曲线y=f(x)=2x2上一点A(2,8),则点A处的切线斜率为___.8当Δx无限趋近于0时,8+2Δx无限趋近于8,
∴曲线f(x)在点A处的切线斜率为8.123452.任一做直线运动的物体,其位移S与时间t的关系是S=3t-t2,则物体的初速度是___.3答案解析12345答案解析3.已知物体运动的速度与时间之间的关系:v(t)=t2+2t+2,则在时间段[1,1+Δt]内的平均加速度是_______,在t=1时的瞬时加速度是___.4+Δt412345答案解析4.已知曲线y=2x2+4x在点P处的切线斜率为16,则点P的坐标为______.(3,30)当Δx无限趋近于0时,4x0+4+2Δx无限趋近于4x0+4,
令4x0+4=16,得x0=3,
∴P(3,30).123455.已知函数y=f(x)在x=x0处的导数为11,则当Δx趋近于零时,
无限趋近于常数______.答案解析-111.曲线的切线斜率是割线斜率的极限值,是函数在一点处的瞬时变化率.
2.瞬时速度是运动物体的位移对于时间的瞬时变化率,可以精确刻画物体在某一时刻运动的快慢程度.规律与方法
2.会求物体运动的瞬时速度与瞬时加速度.问题导学达标检测题型探究内容索引问题导学知识点一 曲线上一点处的切线思考 如图,当点Pn(xn,f(xn))(n=1,2,3,4)沿着曲线f(x)趋近于点P(x,f(x))时,割线PPn的变化趋势是什么?答案 当点Pn趋近于点P时,割线PPn趋近于确定的位置.这个确定的位置的直线PT称为过点P的切线.斜率梳理 可以用逼近的方法来计算切线的斜率,
设P(x,f(x)),Q(x+Δx,f(x+Δx)),当Δx无限趋近于0时, 无限趋近于点P(x,f(x))处的切线的
.知识点二 瞬时速度与瞬时加速度思考 瞬时速度和瞬时加速度和函数的变化率有什么关系?
答案 瞬时速度是位移对于时间的瞬时变化率,瞬时加速度是速度对于时间的瞬时变化率.梳理 (1)如果当Δt无限趋近于0时,运动物体位移S(t)的平均变化率
无限趋近于一个常数,那么这个常数称为物体在t=t0时的 ,即位移对于时间的 .(2)如果当Δt无限趋近于0时,运动物体速度v(t)的平均变化率
无限趋近于一个常数,那么这个常数称为物体在t=t0时的 ,即速度对于时间的 .瞬时速度瞬时变化率瞬时加速度瞬时变化率1.曲线上给定一点P,过点P可以作该曲线的两条割线.( )
2.过曲线上任一点可能作不出一条切线.( )
3.有的曲线过它上面的某一点可作两条切线.( )
4.平均速度刻画运动物体在某一时间段内变化的快慢程度,瞬时速度刻画物体在某一时刻变化的快慢程度.( )[思考辨析 判断正误]√×√√题型探究类型一 求曲线在某点处的切线斜率解答(1)点P处的切线的斜率;即点P处的切线的斜率为22=4.解答即12x-3y-16=0.(2)点P处的切线方程.反思与感悟 解决此类问题的关键是理解割线逼近切线的思想.即求曲线上一点处切线的斜率时,先表示出曲线在该点处的割线的斜率,则当Δx无限趋近于0时,可得到割线的斜率逼近切线的斜率.跟踪训练1 利用割线逼近切线的方法分别求曲线y=2x2在x=0,x=-1,x=2处的切线斜率.当Δx无限趋近于0时,kPQ无限趋近于4x0,从而曲线y=f(x)在x=0,x=-1,x=2处的切线斜率分别为0,-4,8.解答解 设P(x0,f(x0)),Q(x0+Δx,f(x0+Δx)),类型二 求瞬时速度、瞬时加速度解答例2 已知质点M的运动速度与运动时间的关系为v=3t2+2(速度单位:cm/s,时间单位:s),
(1)当t=2,Δt=0.01时,求 ;解答(2)求质点M在t=2 s时的瞬时加速度.解 当Δt无限趋近于0时,6t+3Δt无限趋近于6t,则质点M在t=2 s时的瞬时加速度为12 cm/s2.反思与感悟 (1)求瞬时速度的关键在于正确表示“位移的增量与时间增量的比值”,求瞬时加速度的关键在于正确表示“速度的增量与时间增量的比值”,注意二者的区别.
(2)求瞬时加速度:①求平均加速度 ;②令Δt→0,求出瞬时加速度.跟踪训练2 质点M按规律S(t)=at2+1做直线运动(位移单位:m,时间单位:s).若质点M在t=2 s时的瞬时速度为8 m/s,求常数a的值.解答解 ∵ΔS=S(2+Δt)-S(2)
=a(2+Δt)2+1-a·22-1=4aΔt+a(Δt)2,当Δt无限趋近于0时,4a+aΔt无限趋近于4a.
∵在t=2 s时,瞬时速度为8 m/s,
∴4a=8,∴a=2.达标检测答案12345解析1.已知曲线y=f(x)=2x2上一点A(2,8),则点A处的切线斜率为___.8当Δx无限趋近于0时,8+2Δx无限趋近于8,
∴曲线f(x)在点A处的切线斜率为8.123452.任一做直线运动的物体,其位移S与时间t的关系是S=3t-t2,则物体的初速度是___.3答案解析12345答案解析3.已知物体运动的速度与时间之间的关系:v(t)=t2+2t+2,则在时间段[1,1+Δt]内的平均加速度是_______,在t=1时的瞬时加速度是___.4+Δt412345答案解析4.已知曲线y=2x2+4x在点P处的切线斜率为16,则点P的坐标为______.(3,30)当Δx无限趋近于0时,4x0+4+2Δx无限趋近于4x0+4,
令4x0+4=16,得x0=3,
∴P(3,30).123455.已知函数y=f(x)在x=x0处的导数为11,则当Δx趋近于零时,
无限趋近于常数______.答案解析-111.曲线的切线斜率是割线斜率的极限值,是函数在一点处的瞬时变化率.
2.瞬时速度是运动物体的位移对于时间的瞬时变化率,可以精确刻画物体在某一时刻运动的快慢程度.规律与方法
