2018_2019学年高中数学第1章计数原理1.3二项式定理1.3.1二项式定理课件新人教B版选修2_3(35张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第1章计数原理1.3二项式定理1.3.1二项式定理课件新人教B版选修2_3(35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 989.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 09:39:21 | ||
图片预览









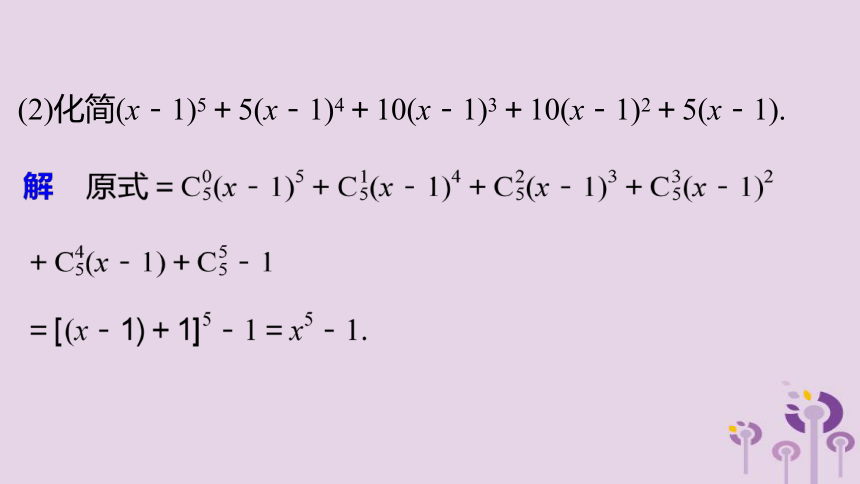

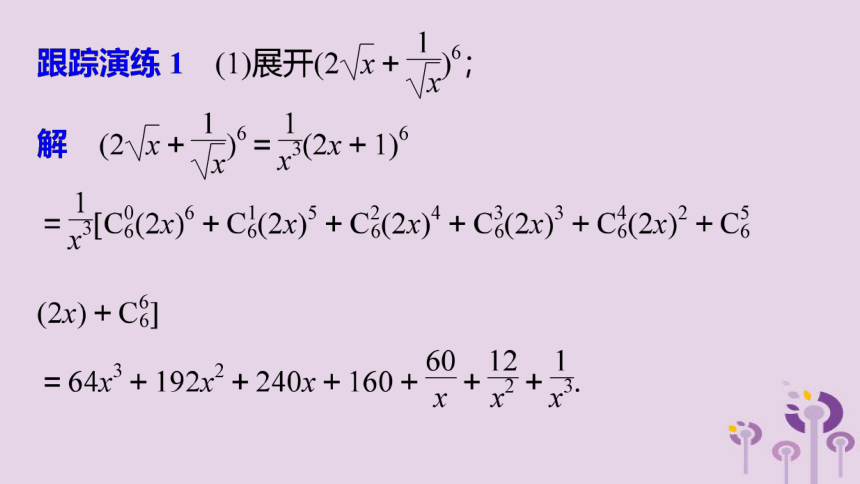
文档简介
课件35张PPT。第一章——计数原理1.3 二项式定理
1.3.1 二项式定理[学习目标]
1.能用计数原理证明二项式定理.
2.掌握二项式定理及其展开式的通项公式.
3.会用二项式定理解决与二项展开式有关的简单问题.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.二项式定理中,项的系数与二项式答 二项式系数与项的系数完全是不同的两个概念.二项式系数是指 它只与各项的项数有关,而与a,b的值无关,而项的系数是指该项中除变量外的常数部分,它不仅与各项的项数有关,而且也与a,b的值有关.2.二项式(a+b)n与(b+a)n展开式中第r+1项是否相同?[预习导引]
1.二项式定理
(a+b)n= ,这个公式所表示的规律叫做二项式定理,等号右边的多项式叫做(a+b)n的 , 它一共有 项,其中各项系数
(r=0,1,2,…,n)叫做展开式的二项式系数.二项展开式n+12.二项展开式的通项
二项展开式中的 项叫做二项展开式的通项,通项是展开式的第r+1项,即Tr+1= .(其中0≤r≤n,r∈N,n∈N+)要点一 二项式定理的正用、逆用(2)化简(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1).规律方法 运用二项式定理展开二项式,要记准展开式的通项公式,对于较复杂的二项式,有时先化简再展开更简捷;要搞清楚二项展开式中的项以及该项的系数与二项式系数的区别.逆用二项式定理可将多项式化简,对于这类问题的求解,要熟悉公式的特点、项数、各项幂指数的规律以及各项的系数.要点二 二项展开式通项的应用
例2 若 展开式中前三项系数成等差数列,求:
(1)展开式中含x的一次项;即n2-9n+8=0,
解得n=8,或n=1(舍去).(2)展开式中的所有有理项.则r=0,4,8,规律方法 利用二项式的通项公式求二项展开式中具有某种特征的项是关于二项式定理的一类典型题型.常见的有求二项展开式中的第r项、常数项、含某字母的r次方的项等等.其通常解法就是根据通项公式确定Tr+1中r的值或取值范围以满足题设的条件.跟踪演练2 已知在 n的展开式中,第6项为常数项.
(1)求含x2的项的系数;∴n=10.(2)求展开式中所有的有理项.∵r∈N,
∴k应为偶数.
又∵0≤r≤10,
∴k可取2,0,-2,即r=2,5,8.要点三 二项式定理的应用
例3 (1)用二项式定理证明:34n+2+52n+1能被14整除;
(2)求9192除以100的余数.
证明 34n+2+52n+1=92n+1+52n+1
=(14-5)2n+1+52n+1上式是14的倍数,能被14整除,所以34n+2+52n+1能被14整除.(2)求9192除以100的余数.
∵992=(10-1)92∴被100除的余数为81,即9192除以100的余数为81.可知前面各项均能被100整除,只有末尾两项不能被100整除,由于C ×90+1=8 281=8 200+81,
故9192除以100的余数为81.规律方法 利用二项式定理可以解决求余数和整除的问题,通常需将底数化成两数的和与差的形式,且这种转化形式与除数有密切的关系.跟踪演练3 求证:5151-1能被7整除.
证明 ∵5151-1=(49+2)51-1显然能被7整除,所以(5151-1)能被7整除.1.若(1+ )4=a+b (a,b为有理数),则a+b等于( )
A.33 B.29 C.23 D.19123123又∵a,b为有理数,
∴a=17,b=12.
∴a+b=29.
答案 B1232.在(1-x)5-(1-x)6的展开式中,含x3的项的系数是( )
A.-5 B.5 C.-10 D.10故(1-x)5-(1-x)6的展开式中x3的系数为10.D1233.求证32n+2-8n-9(n∈N+)能被64整除.
证明 32n+2-8n-9
=(8+1)n+1-8n-9123该式每一项都含因式82,故能被64整除.课堂小结
1.注意区分项的二项式系数与系数的概念.
2.要牢记C an-rbr是展开式的第r+1项,不要误认为是第r项.
3.求解特定项时必须合并通项公式中同一字母的指数,根据具体要求,令其为特定值.
1.3.1 二项式定理[学习目标]
1.能用计数原理证明二项式定理.
2.掌握二项式定理及其展开式的通项公式.
3.会用二项式定理解决与二项展开式有关的简单问题.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功[知识链接]
1.二项式定理中,项的系数与二项式答 二项式系数与项的系数完全是不同的两个概念.二项式系数是指 它只与各项的项数有关,而与a,b的值无关,而项的系数是指该项中除变量外的常数部分,它不仅与各项的项数有关,而且也与a,b的值有关.2.二项式(a+b)n与(b+a)n展开式中第r+1项是否相同?[预习导引]
1.二项式定理
(a+b)n= ,这个公式所表示的规律叫做二项式定理,等号右边的多项式叫做(a+b)n的 , 它一共有 项,其中各项系数
(r=0,1,2,…,n)叫做展开式的二项式系数.二项展开式n+12.二项展开式的通项
二项展开式中的 项叫做二项展开式的通项,通项是展开式的第r+1项,即Tr+1= .(其中0≤r≤n,r∈N,n∈N+)要点一 二项式定理的正用、逆用(2)化简(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1).规律方法 运用二项式定理展开二项式,要记准展开式的通项公式,对于较复杂的二项式,有时先化简再展开更简捷;要搞清楚二项展开式中的项以及该项的系数与二项式系数的区别.逆用二项式定理可将多项式化简,对于这类问题的求解,要熟悉公式的特点、项数、各项幂指数的规律以及各项的系数.要点二 二项展开式通项的应用
例2 若 展开式中前三项系数成等差数列,求:
(1)展开式中含x的一次项;即n2-9n+8=0,
解得n=8,或n=1(舍去).(2)展开式中的所有有理项.则r=0,4,8,规律方法 利用二项式的通项公式求二项展开式中具有某种特征的项是关于二项式定理的一类典型题型.常见的有求二项展开式中的第r项、常数项、含某字母的r次方的项等等.其通常解法就是根据通项公式确定Tr+1中r的值或取值范围以满足题设的条件.跟踪演练2 已知在 n的展开式中,第6项为常数项.
(1)求含x2的项的系数;∴n=10.(2)求展开式中所有的有理项.∵r∈N,
∴k应为偶数.
又∵0≤r≤10,
∴k可取2,0,-2,即r=2,5,8.要点三 二项式定理的应用
例3 (1)用二项式定理证明:34n+2+52n+1能被14整除;
(2)求9192除以100的余数.
证明 34n+2+52n+1=92n+1+52n+1
=(14-5)2n+1+52n+1上式是14的倍数,能被14整除,所以34n+2+52n+1能被14整除.(2)求9192除以100的余数.
∵992=(10-1)92∴被100除的余数为81,即9192除以100的余数为81.可知前面各项均能被100整除,只有末尾两项不能被100整除,由于C ×90+1=8 281=8 200+81,
故9192除以100的余数为81.规律方法 利用二项式定理可以解决求余数和整除的问题,通常需将底数化成两数的和与差的形式,且这种转化形式与除数有密切的关系.跟踪演练3 求证:5151-1能被7整除.
证明 ∵5151-1=(49+2)51-1显然能被7整除,所以(5151-1)能被7整除.1.若(1+ )4=a+b (a,b为有理数),则a+b等于( )
A.33 B.29 C.23 D.19123123又∵a,b为有理数,
∴a=17,b=12.
∴a+b=29.
答案 B1232.在(1-x)5-(1-x)6的展开式中,含x3的项的系数是( )
A.-5 B.5 C.-10 D.10故(1-x)5-(1-x)6的展开式中x3的系数为10.D1233.求证32n+2-8n-9(n∈N+)能被64整除.
证明 32n+2-8n-9
=(8+1)n+1-8n-9123该式每一项都含因式82,故能被64整除.课堂小结
1.注意区分项的二项式系数与系数的概念.
2.要牢记C an-rbr是展开式的第r+1项,不要误认为是第r项.
3.求解特定项时必须合并通项公式中同一字母的指数,根据具体要求,令其为特定值.
