2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.1.2指数函数及其性质课件新人教A版必修1(17张)
文档属性
| 名称 | 2018_2019学年高中数学第二章基本初等函数(Ⅰ)2.1.2指数函数及其性质课件新人教A版必修1(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 385.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-27 09:38:55 | ||
图片预览






文档简介
课件17张PPT。2.1.2指数函数及其性质课本48页问题1中函数
的解析式与问题2中函数
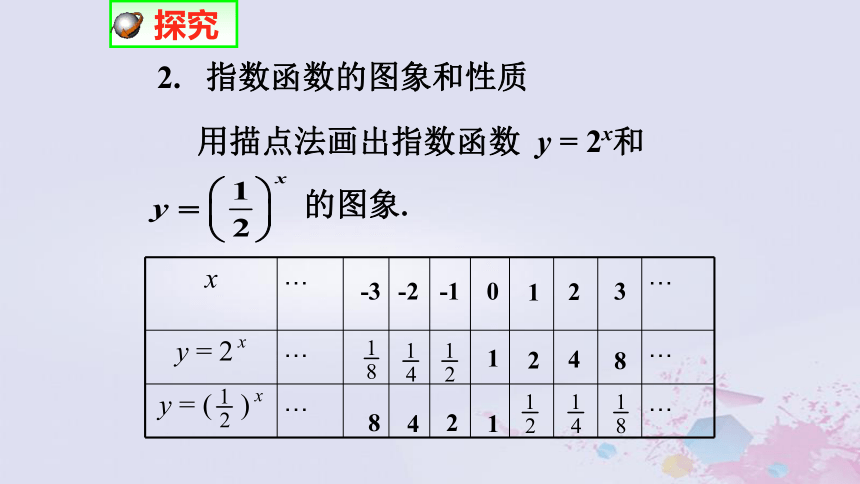
的解析式有什么共同特征? 探究 如果用a来代替 和1.073,那么以上两个函数的解析式都可以表示为的形式,其中自变量x是指数,底数a是一个大于0且不等于1的常量.1.指数函数的定义: 一般地,函数 y = a x (a>0,且a≠1)叫做指数函数(exponential fun_ction),其中x是自变量,函数的定义域是R. 理论1.下列函数中,那些是指数函数? .(1) (5) (6) (8) 练习 用描点法画出指数函数 y = 2x和
的图象.2. 指数函数的图象和性质-301112-1224-24388 探究-3 -2 -1 o 1 2 3 x8 7 6 5 4 3 2 1yy = 2 xy = ( ) x(-3,8)(-2,4)(-1,2)( 0,1)(1, )(2, )(3, )(3,8)(2,4)(1,2)( 0,1)(-1, )(-2, )(-3, )y=2x 两个函数图象关于 y 轴对称! 函数 y =2x的图象和函数 的图象有什么关系?可否利用 y =2x 的图象画出
的图象? 思考yxa>100,且a≠1)的图象和性质: 例1 已知指数函数f (x)=ax(a>0,且a≠1)
的图象经过点(3,π),求f (0),f (1),f (-3)的值. 分析:f (0)、f (1)、f (-3)的值,我们需要先求出指数函数f (x)=ax 的解析式,也就是要先求a的值.根据函数图像过点(3,π)这一条件,可以求得底数a的值. 举例 解:因为f (x)=ax 的图象过点(3,π),
所以f (3)=π, 即a3= π,解得 ,于是
所以f (0) =π0 =1, 例2 比较下列各题中两个值的大小:
(1) 1.72.5, 1.73;
(2) 0.8-0.1, 0.8-0.2;
(3) 1.70.3, 0.93.1. 举例解:(1) 考察指数函数y=1.7 x .由于底数1.7>1 ,所以指数函数在R上是增函数.∵2.5<3, ∴1.7 2.5<1.7 3;(2) 0.8 – 0.1<0.8 – 0.2;(3) 由指数函数的性质知
1.7 0.3>1.7 0=1 , 0.9 3.1<0.9 0=1,即1.7 0.3>1 , 0.9 3.1<1 , ∴1.7 0.3>0.9 3.1 . 练习例3 截止到1999年底,我国人口约13亿.如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)? 举例y= 13(1+1%)x 解:设今后人口平均增长率为1%,
经过x年后,我国人口数为y亿.2. 设y1=a3x+1,y2=a-2x,其中a>0且a?1,确定x为何值时,有
(1)y1=y2 ; (2)y1>y2. 练习1.指数函数的定义;
2.指数函数简图的作法以及应注意的地方;
3.指数函数的图象和性质. 小结
的解析式与问题2中函数
的解析式有什么共同特征? 探究 如果用a来代替 和1.073,那么以上两个函数的解析式都可以表示为的形式,其中自变量x是指数,底数a是一个大于0且不等于1的常量.1.指数函数的定义: 一般地,函数 y = a x (a>0,且a≠1)叫做指数函数(exponential fun_ction),其中x是自变量,函数的定义域是R. 理论1.下列函数中,那些是指数函数? .(1) (5) (6) (8) 练习 用描点法画出指数函数 y = 2x和
的图象.2. 指数函数的图象和性质-301112-1224-24388 探究-3 -2 -1 o 1 2 3 x8 7 6 5 4 3 2 1yy = 2 xy = ( ) x(-3,8)(-2,4)(-1,2)( 0,1)(1, )(2, )(3, )(3,8)(2,4)(1,2)( 0,1)(-1, )(-2, )(-3, )y=2x 两个函数图象关于 y 轴对称! 函数 y =2x的图象和函数 的图象有什么关系?可否利用 y =2x 的图象画出
的图象? 思考yxa>10
的图象经过点(3,π),求f (0),f (1),f (-3)的值. 分析:f (0)、f (1)、f (-3)的值,我们需要先求出指数函数f (x)=ax 的解析式,也就是要先求a的值.根据函数图像过点(3,π)这一条件,可以求得底数a的值. 举例 解:因为f (x)=ax 的图象过点(3,π),
所以f (3)=π, 即a3= π,解得 ,于是
所以f (0) =π0 =1, 例2 比较下列各题中两个值的大小:
(1) 1.72.5, 1.73;
(2) 0.8-0.1, 0.8-0.2;
(3) 1.70.3, 0.93.1. 举例解:(1) 考察指数函数y=1.7 x .由于底数1.7>1 ,所以指数函数在R上是增函数.∵2.5<3, ∴1.7 2.5<1.7 3;(2) 0.8 – 0.1<0.8 – 0.2;(3) 由指数函数的性质知
1.7 0.3>1.7 0=1 , 0.9 3.1<0.9 0=1,即1.7 0.3>1 , 0.9 3.1<1 , ∴1.7 0.3>0.9 3.1 . 练习例3 截止到1999年底,我国人口约13亿.如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)? 举例y= 13(1+1%)x 解:设今后人口平均增长率为1%,
经过x年后,我国人口数为y亿.2. 设y1=a3x+1,y2=a-2x,其中a>0且a?1,确定x为何值时,有
(1)y1=y2 ; (2)y1>y2. 练习1.指数函数的定义;
2.指数函数简图的作法以及应注意的地方;
3.指数函数的图象和性质. 小结
